Real reserves in Uniswap v3

In the last chapter, we introduced two new concepts: real reserves and virtual reserves. The real reserves of a segment are the amount of tokens contained in that segment— $x_r$ tokens X, $y_r$ tokens Y, or both.

The virtual reserves are the amount of tokens that the segment would have if it were part of an infinite curve. Virtual reserves are necessary because swaps in curve segments in Uniswap v3 behave exactly as in Uniswap v2—that is, as if the segments were actually part of an infinite curve in a pool on Uniswap v2.

We also derived formulas to calculate the virtual reserves of a segment based on price and liquidity, but what we want is a formula to calculate the real reserves of a segment. This is the main goal of this chapter.

Liquidity, Price and virtual reserves in Uniswap v3

In Uniswap v3, liquidity and price are defined as follows:

$$ \begin{align*} &L^2 = xy \\ &p= \frac{y}{x} \end{align*}$$

where $x$ and $y$ are the virtual reserves and $p$ is the price of token X in units of token X.

As we saw in the previous chapter, we can invert these formulas and derive the virtual reserves $x$ and $y$ from $L$ and $\sqrt{p}$, as:

$$ \begin{align*} &x = \frac{L}{\sqrt{p}} \\ &y= L \sqrt{p} \end{align*}$$

This isn’t enough information to derive the real reserves of a segment, since all segments with the same liquidity and at the same price will have the same virtual reserves—regardless of their boundaries.

This can be seen in the animation below, which illustrates two segments with the same liquidity at the same price. Their virtual reserves are the same, but their real reserves are not.

Thus, we can’t derive the real reserves only from the price and liquidity — the segment boundaries must also be taken into account.

The real reserves of a segment

The real reserves of a segment are the amount of tokens available to be traded against in the segment until the price reaches the segment’s boundaries.

Consider the situation illustrated below, where the price is within the segment (left side). At this moment, the pool has $x_r$ real reserves in tokens X and $y_r$ reserves in token Y.

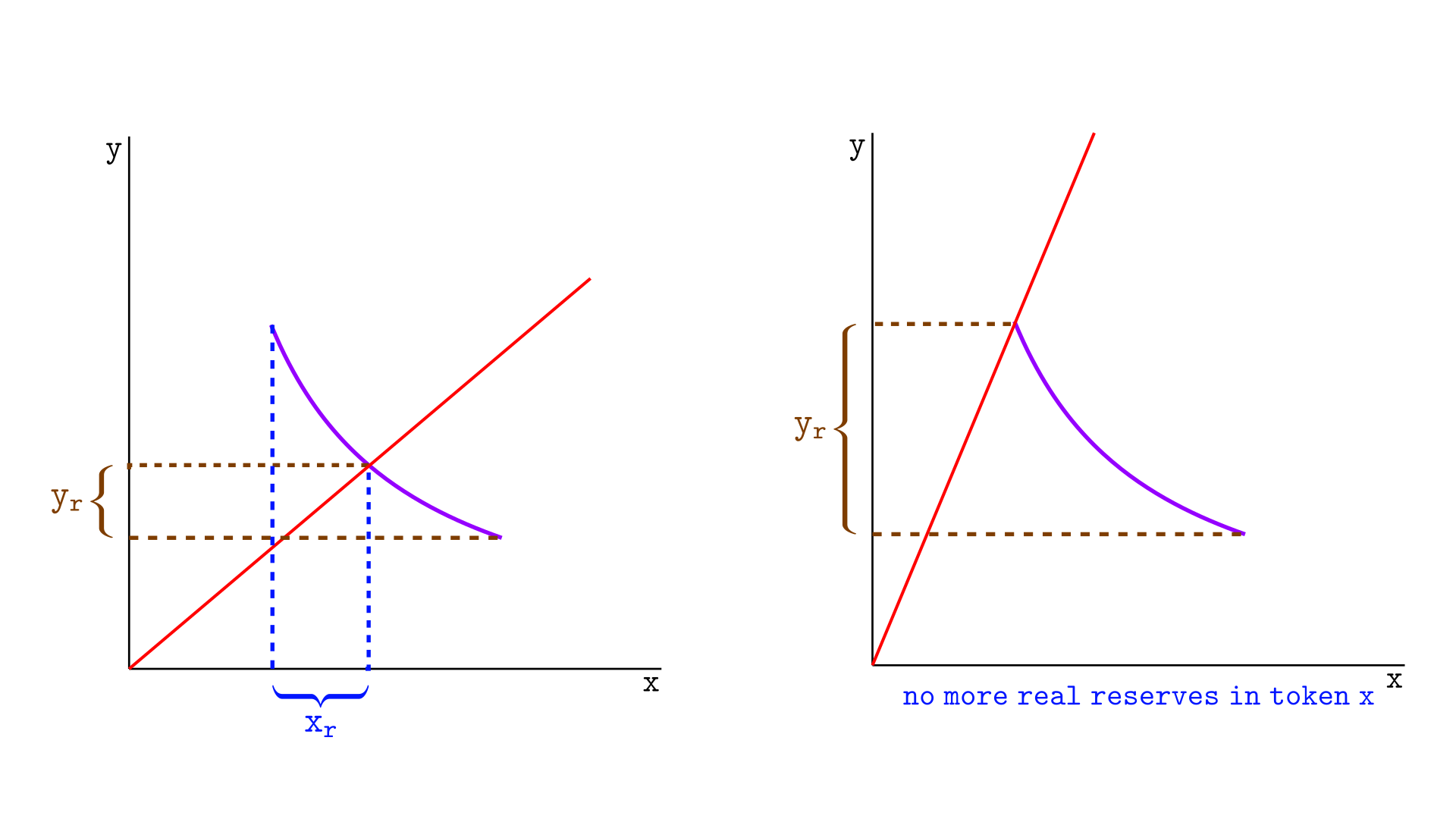
On the right side of the above image, a swap causes the price to move to the upper tick, and the pool now holds reserves only in tokens Y—no longer in tokens X.

This shows that the real reserves of tokens X in a segment, $x_r$, are the amount of tokens that will leave the segment during a swap that moves the price to the upper tick.

The same logic can be applied to the real reserves in tokens Y, but now for a swap that moves the price to the lower tick, as illustrated below.

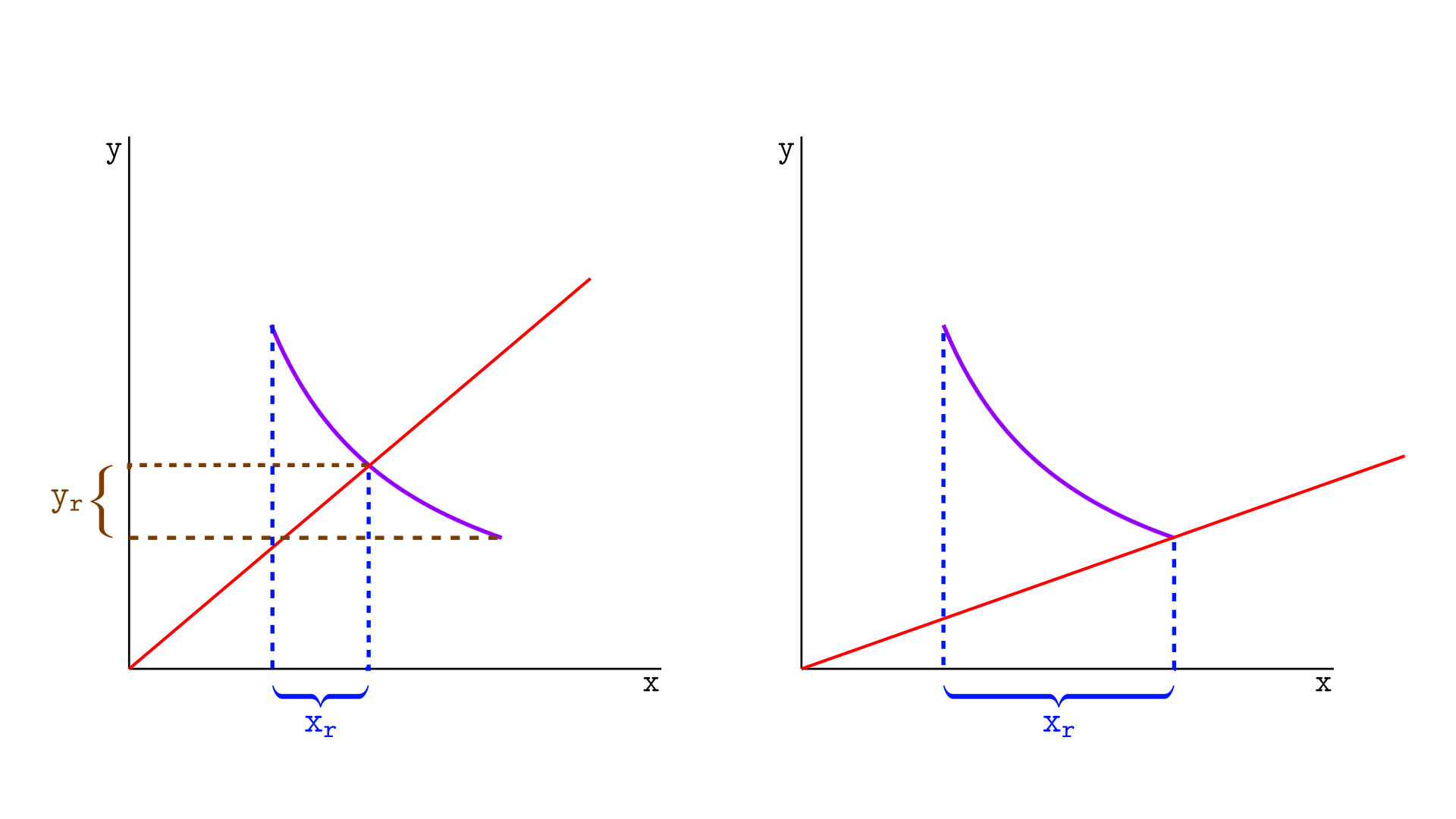
The real reserves of $y$, $y_r$, are the amount of tokens that will leave the segment during a swap that moves the price to the lower tick.

Thus, if we can calculate how many tokens X left the pool in the first example, and how many tokens Y left the pool in the second, we will have derived a formula for the real reserves.

And we can do this, because we know how to perform these calculations in Uniswap v2—and within a segment, Uniswap v3 behaves exactly like Uniswap v2.

Deriving the formula for the real reserves of token X

In the context of an infinite curve, we can easily calculate the amount of tokens X that leave the pool in a swap that moves the price. Let us consider that the price starts at $p$ and moves to $p_u$, where $p_u$ is the price at the upper tick, as illustrated below.

On the left, the virtual reserves in X are given by $x$ (virtual reserves at $p)$. On the right, the virtual reserves are given by $x_u$ (virtual reserves at $p_u$). In Uniswap v2, these are the actual reserves, so that $x-x_u$ tokens will leave the pool in this swap.

Since Uniswap v3 has the same behavior as v2, then $x-x_u$ tokens will leave the pool also in Uniswap v3 – these are the real reserves in X of this segment, $x_r$.

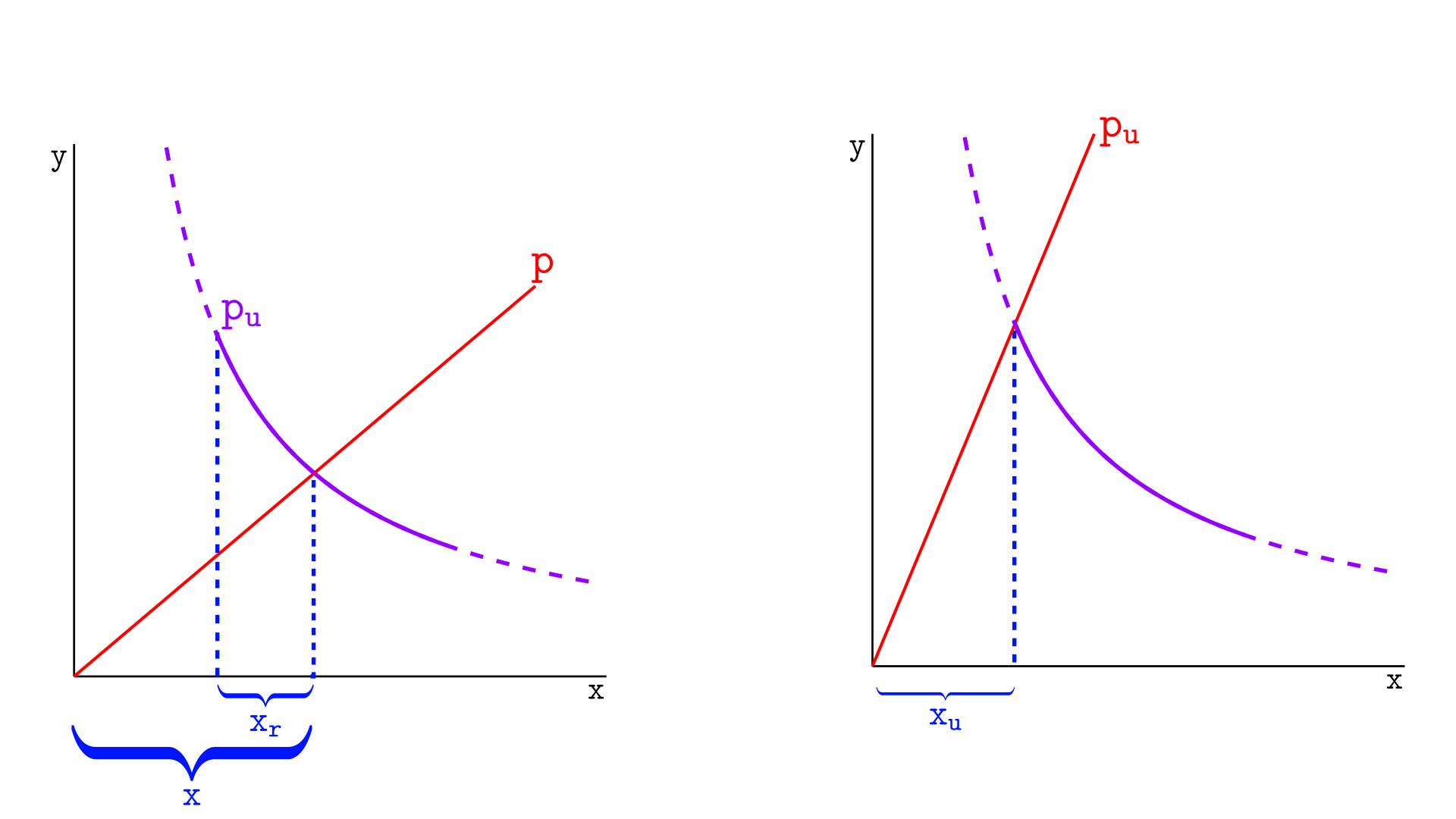
Thus,

$$ x_r=x-x_u$$

And we know how to calculate virtual reserves based on liquidity and price. Remember that $x=L/\sqrt{p}$. So by substitution, we have that

$$ \begin{align*} x_r &= x -x_u \\ &= \frac{L}{\sqrt{p}} -\frac{L}{\sqrt{p_u}} \end{align*}$$

Since $p$ is less than or equal to $p_u$, $x_r$ will always be positive or zero. The real reserves of X become zero when $p$ reaches the upper tick $p_u$, as expected.

Calculating $x_r$ when the current price is not within the segment

Let us consider the cases where $p$ is not within the segment.

Current price below the lower tick

If the current price is below the lower tick, the real reserves of the segment are the difference between the virtual reserves at the lower tick, $p_l$, and at the upper tick, $p_u$, as illustrated below. This is the case because we can assume that $p$ will eventually reach $p_l$, and swaps from $p$ to $p_l$ do not interfere with the segment – we need to take into account only the swap from $p_l$ to $p_u$.

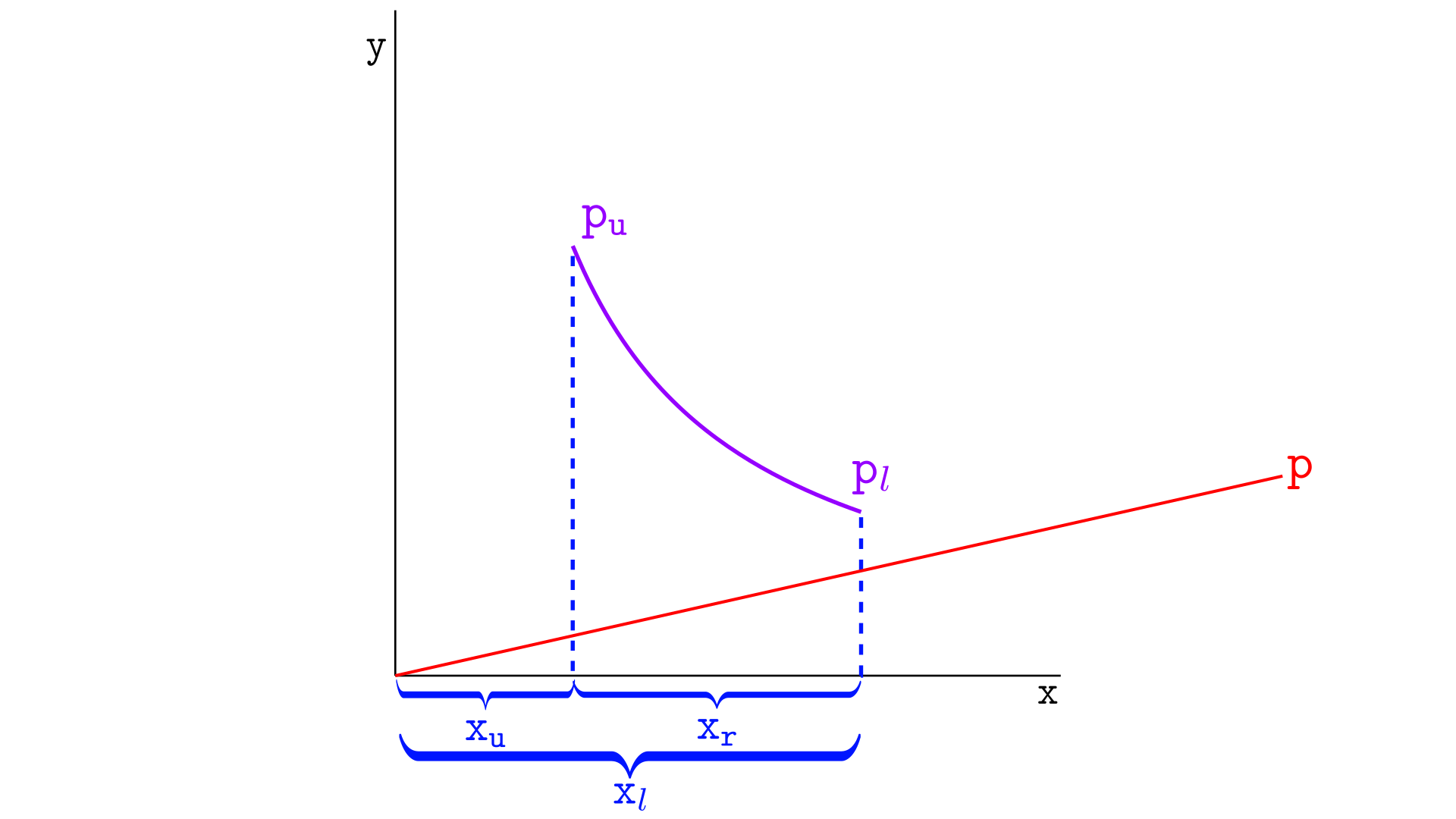
By substituting $x=L/\sqrt{p}$, we have the real reserves as:

$$ \begin{align*} x_r &= x_l -x_u \\ &= \frac{L}{\sqrt{p_l}} -\frac{L}{\sqrt{p_u}} \end{align*}$$

Current price above the upper tick

If the current price is higher than the upper tick, the segment has no reserves in token X, so the real reserves $x_r$ are zero.

As you can see, the real reserves in tokens X depend not only on the current price and liquidity, but also on the upper and lower ticks.

Deriving the formula for the real reserves of token Y

To calculate the real reserves in tokens Y of a segment, we will follow the same strategy we used for tokens X. Let us consider the illustration below. When the price is at $p$, we have $y_r$ tokens Y in the segment – the real reserves in Y – as shown on the left, and the virtual reserves are denoted by $y$.

A swap that moves the price to the lower tick $p_l$ will remove all tokens Y from the segment. Thus, to calculate $y_r$, we only need to compute the amount of tokens Y that leave the segment in a swap between $p$ and $p_l$.

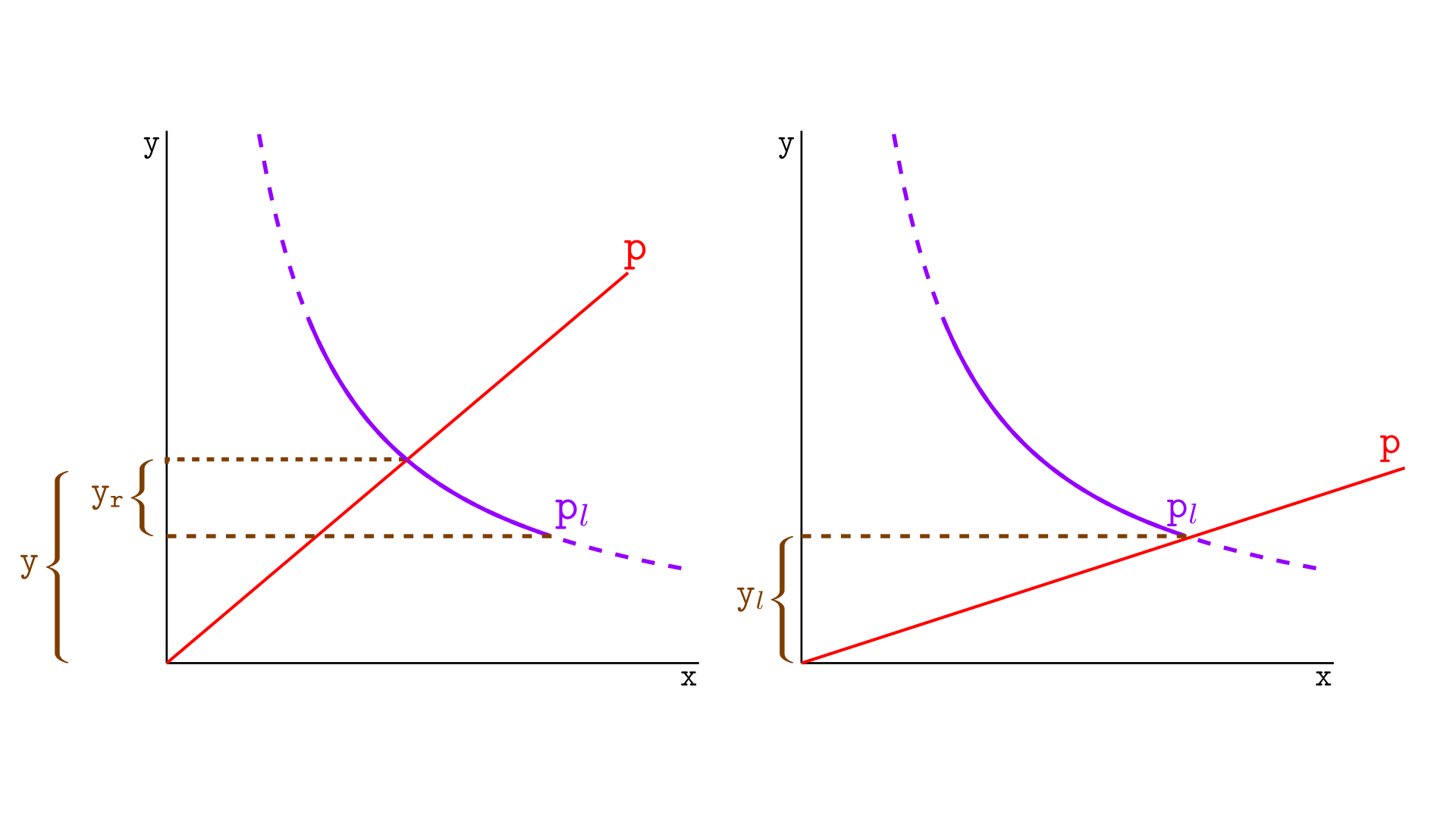
The swap will change the virtual reserves from $y$ to $y_l$, so the real reserves in this case are calculated as $y-y_l$. Remembering that virtual reserves in tokens Y are given by $y = L \sqrt{p}$, we have that

$$ \begin{align*} y_r &= y-y_l \\ &= L\sqrt{p} – L\sqrt{p_l} \end{align*}$$

Since $p$ is greater or equal than $p_l$, $y_r$ will always be positive or zero. The real reserves in Y become zero when $p$ reaches the lower tick $p_l$, as expected.

Calculating $y_r$ when the current price is not within the segment

Let us consider the two cases where $p$ is not in segment.

Current price above the upper tick

If the price is greater than the upper tick, the real reserves in tokens Y, given by $y_r$, are illustrated below, where $y_u$ are the virtual reserves in Y for the upper tick and $y_l$ are the virtual reserves in Y for the lower tick.

To calculate $y_r$, we need to consider a swap from the upper tick $p_u$ to the lower tick $p_l$, which will take the virtual reserves from $y_u$ to $y_l$.

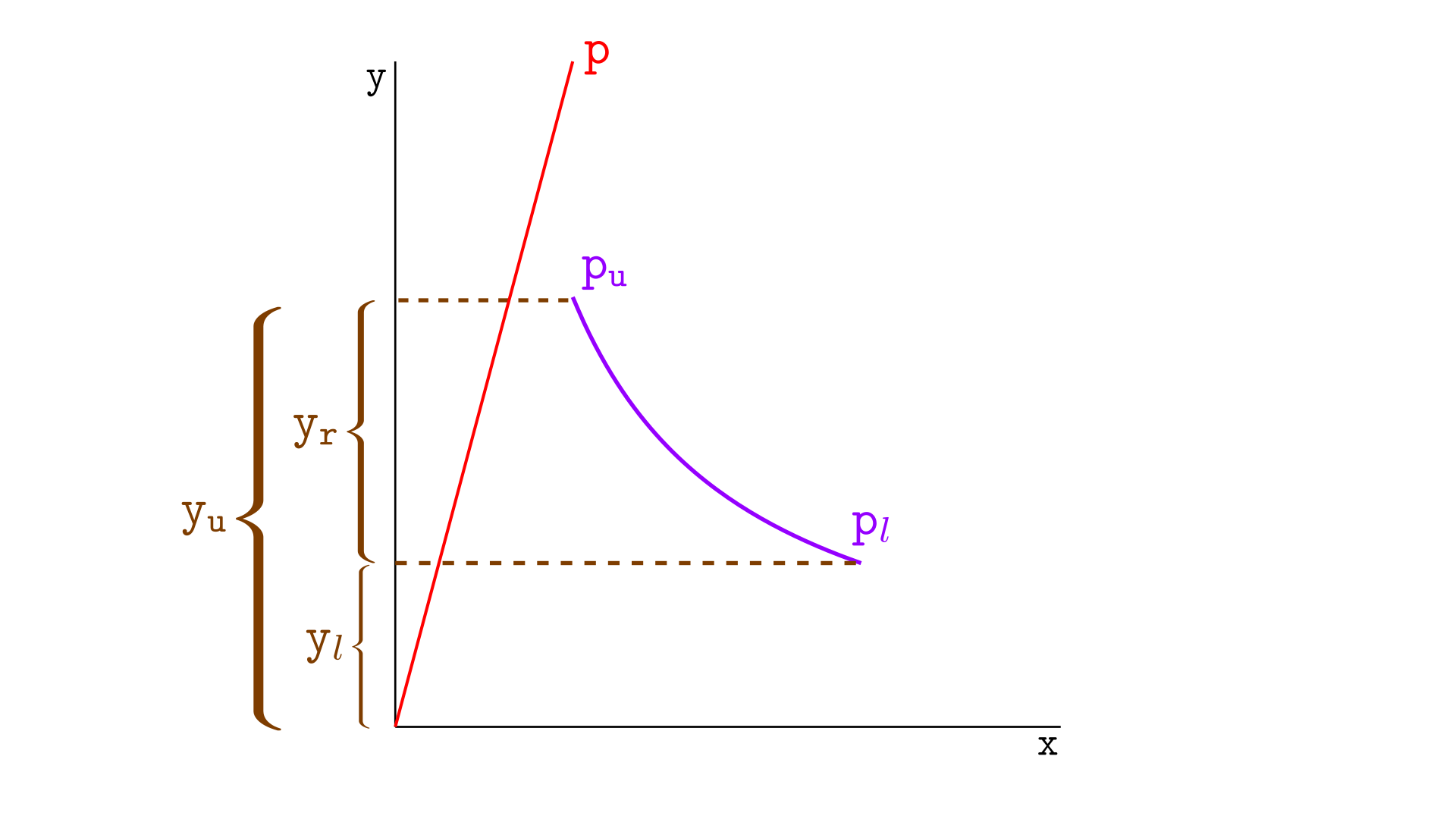
Thus, the real reserves in tokens Y are given by:

$$ \begin{align*} y_r &= y_u-y_l \\ &= L\sqrt{p_u} – L\sqrt{p_l} \end{align*}$$

Current price below the lower tick

If the price is lower than the lower tick, there will be no real reserves in tokens Y, so $y_r$ will be zero.

Calculating the real reserves between two arbitrary prices

Given two arbitrary prices within a segment, we can always calculate the real reserves between them – in other words, the amount of tokens that need to be swapped out to move from one price to the next. The reasoning is the same as above, where we calculated the real reserves of a segment, but we don’t limit ourselves to using the end of the segment as the stop point of the trade.

The real reserves between two prices will also depend on whether the current price is greater than or equal to the highest price, less than or equal to the lowest price, or falls between the two.

Consider calculating the real reserves between prices $p_a$ and $p_b$, where $p_b > p_a$, with current price $p$ and the liquidity between these prices given by $L$. The three cases we need to consider are illustrated below.

1. The current price is below the lower tick
2. The current price is above the upper tick
3. The current price is between the upper and lower ticks

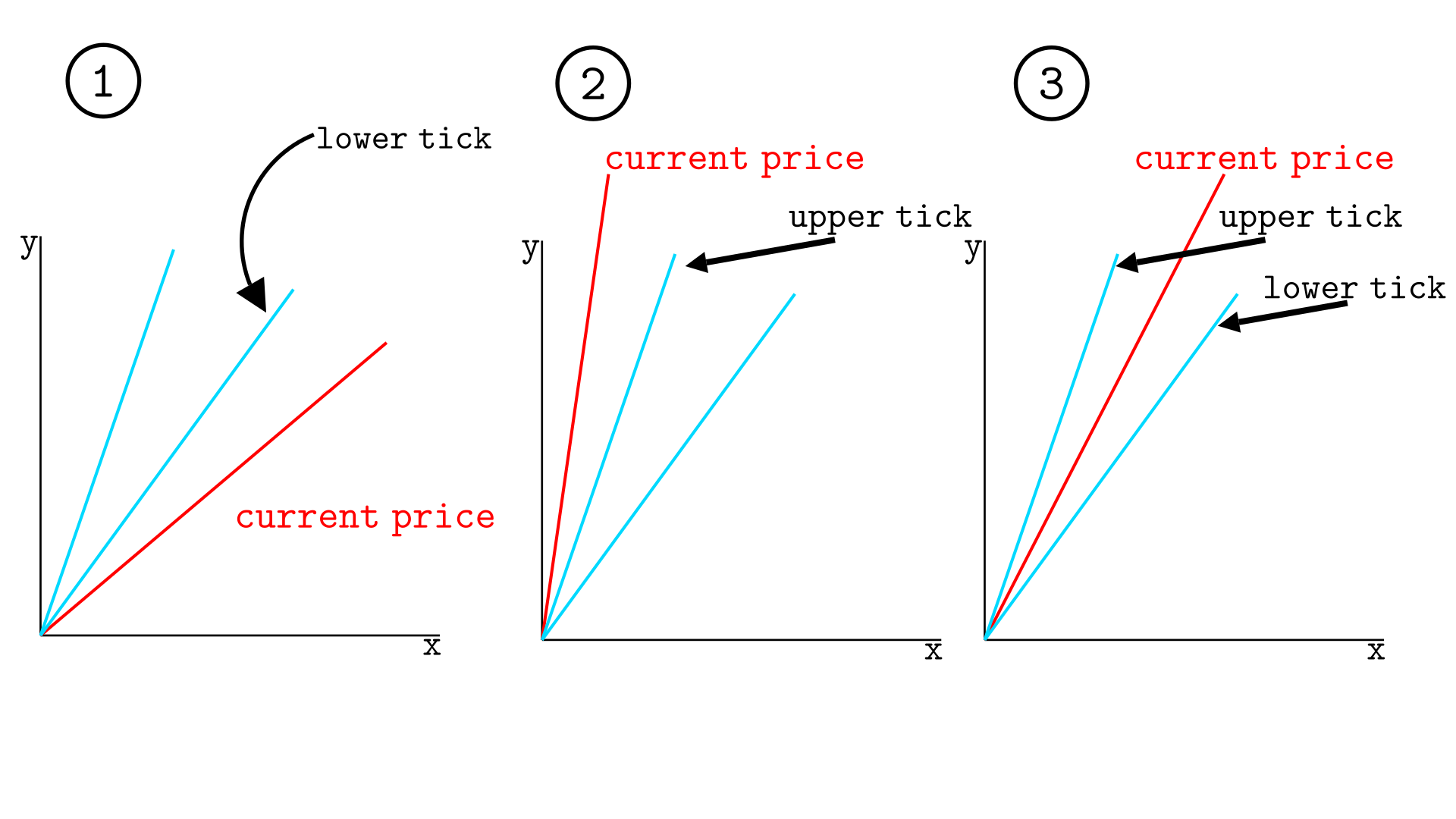
The formulas will be as follows:

1. Current price below the lower tick

In this case, all the real reserves of the segment is in tokens X.

$$ \begin{align*} x_r &= \frac{L}{\sqrt{p_a}} -\frac{L}{\sqrt{p_b}} \\ y_r &= 0 \end{align*}$$

2. Current price above the upper tick

In this case, all the real reserves of the segment is in tokens Y.

$$ \begin{align*} x_r &= 0 \\ y_r &= L \sqrt{p_b} – L \sqrt{p_a} \end{align*}$$

3. Current price between upper and lower ticks

In this case, the segment has both tokens X and Y.

$$ \begin{align*} x_r &= \frac{L}{\sqrt{p}} -\frac{L}{\sqrt{p_b}} \\ y_r &= L\sqrt{p} – L\sqrt{p_a} \end{align*}$$

The protocol uses these formulas to calculate the amount of tokens X or Y present between two prices, given a liquidity $L$.

Using the above formulas in swaps

In Uniswap v2, the protocol doesn’t need to worry about the final price after a swap — the final price is not bounded, since liquidity is constant and the price curve is infinite.

In Uniswap v3, segments are finite and therefore have boundaries. When a swap occurs within a segment, the protocol must calculate how many real reserves that segment has to determine whether the amount the user wants to trade can be obtained entirely in that segment or only partially. It does this by calculating the amount of tokens between the current price and the segment’s boundary — the upper tick if the user is buying tokens X, or the lower tick if the user is selling tokens X.

In later chapters, we will study in detail how swap works in Uniswap v3.

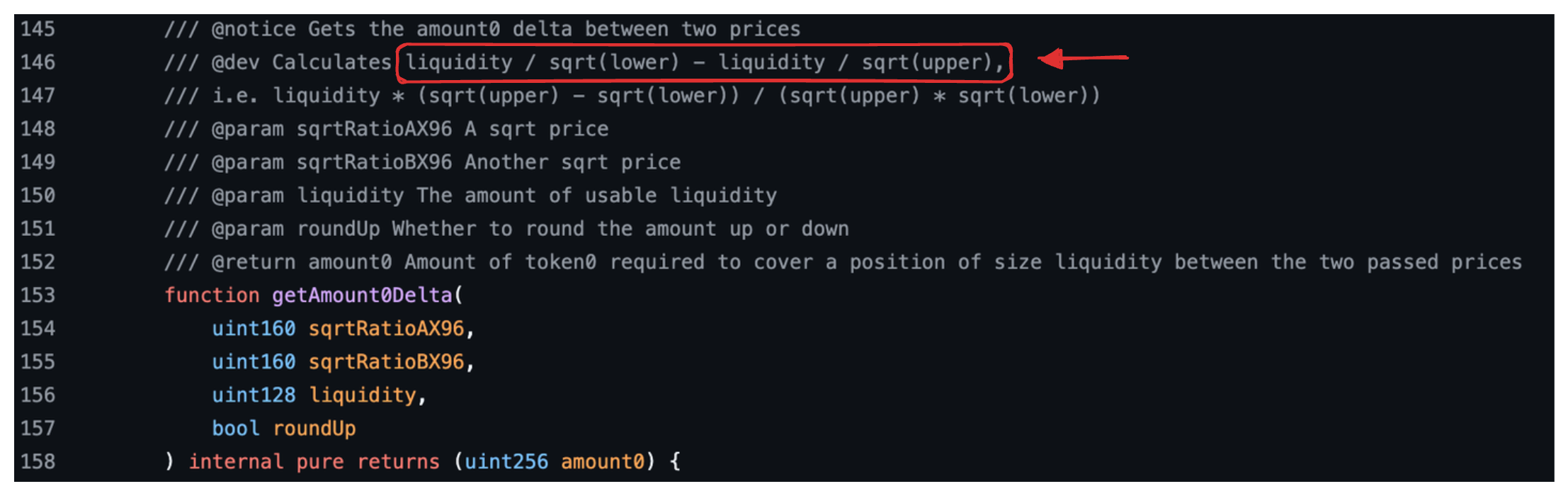
The formulas we derived above can be found in the SqrtPriceMath.sol library. These can be found in the functions getAmount0Delta and getAmount1Delta, whose signatures are shown below along with their NatSpec comments.

getAmount0Delta

This function calculates and returns the amount of tokens X between two prices: a lower price and an upper price. The red box in the text shows the formula we derived above for real reserves in tokens X, $L/\sqrt{p_l} -L/\sqrt{p_u}$.

The function takes the lower price (sqrtRatioAX96), the upper price (sqrtRatioBX96), the segment’s liquidity, and a flag indicating whether the amount should be rounded up or not.

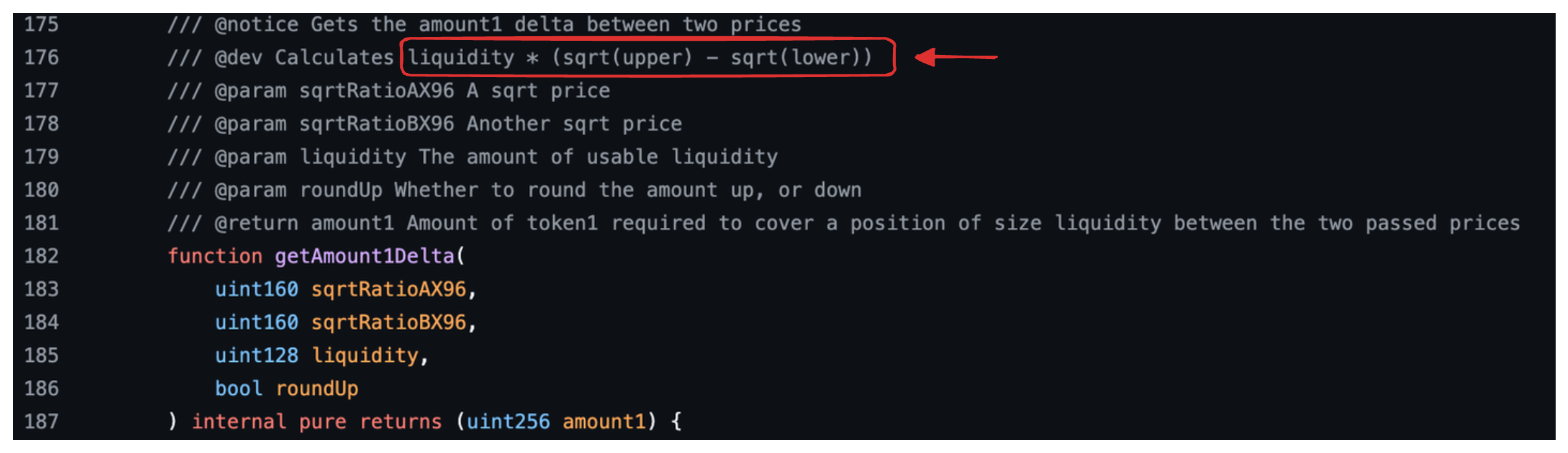
getAmount1Delta

This function calculates and returns the amount of tokens Y between two prices: a lower price and an upper price. Again, the red box in the text shows the formula we derived above, now for real reserves in tokens Y, $L\sqrt{p_u} -L\sqrt{p_l}$.

Summary

• The real reserves of a segment depend not only on liquidity and current price, but also on the upper and lower tick.
• Given two prices $p_a$ and $p_b$, for $p_b > p_a$, the real reserves in tokens X between these two prices are given by $x_r = \frac{L}{\sqrt{p_a}} -\frac{L}{\sqrt{p_b}}$, within a segment with liquidity $L$ and if the current price is less than or equal to $p_a$.
• Given two prices $p_a$ and $p_b$, for $p_b > p_a$, the real reserves in tokens Y between these two prices are given by $y_r = L \sqrt{p_b} – L \sqrt{p_a}$, within a segment with liquidity $L$ and if the current price is greater than or equal to $p_b$.

Exercises

1. Let’s say that the current price is tick zero and there is a segment with liquidity $L=1,000,000,000$ defined between ticks -10 and 10. What are the real reserves in token X and Y for this segment?
2. The same for problem (1), but now the current price is above tick 10.
3. The same for problem (1), but now the current price is below tick -10.