32-Bit Emulation in ZK

The default datatype in ZK is the field element, where all arithmetic is done modulo a large prime number. However, most “real” computation is done using 32, 64, or 256-bit numbers depending on the virtual machine or execution environment.

Why Do We Need 32-Bit Emulation?

Many cryptographic hash functions operate on 32-bit words since, historically, 32 bits was the default word size of many CPUs. This later increased to 64 bits. The EVM uses 256 bits so that it can easily accommodate the keccak256 hash.

If we want to use ZK to prove the correct execution of a traditional hash function or some virtual machine that does not use finite fields (most do not), then we need to “model” traditional datatypes with a field element. Therefore, we use a field element (signal) in Circom to hold a number that cannot exceed what a 32-bit number can hold, even though the signal can hold values much larger than 32 bits.

32-bit words vs finite field elements

The key difference between a 32-bit word and a finite field element is the point at which they overflow. In Circom, or any language using the bn128 curve, the overflow happens at $p$ where $p$ = 21888242871839275222246405745257275088548364400416034343698204186575808495617. In a 32-bit machine, the overflow happens at 4294967296 or, in general, at $2^n$ where $n$ is the number of bits in the virtual machine.

One can think of a 32-bit virtual machine doing all arithmetic modulo $2^{32}$. A normal virtual machine overflows at that number by default. When doing modular arithmetic in a finite field however, computing modulo $2^{32}$ would add quite a few constraints (as we will see later), but luckily, there is a useful math trick to do it efficiently.

The following two functions are equivalent at computing modulo $2^{32}$:

contract DemoMod32 {
  function mod32(uint256 x) public pure returns (uint256) {
    return x % (2**32);
  }

  function mod32e(uint256 x) public pure returns (uint256) {
    // only keep the 32 least significant bits
    return uint256(uint32(x)); 
  }
}

We can compute$\mod 2^{32}$ simply by keeping only the 32 least significant bits. A formal verification of this is in the appendix. Before we do any arithmetic on a signal containing a 32-bit number, we first need to be completely sure that the number held by the signal does, in fact, fit into 32 bits.

The 32-bit range check

If we are creating a ZK circuit that simulates a computation using 32-bit words, then we need to ensure that none of the signals ever hold a value greater than or equal to $2^{32}$. One intuitive thing to do is to use the LessThan template as follows:

signal safe;
safe <== LessThan(252)([x, 2**32]);
safe === 1;

However, this circuit creates more constraints than necessary.

A more efficient approach would be to take advantage of binary representation. The key idea is to encode a number with 32 bits, and if itfits into 32 bits, the circuit executes normally. In contrast, if the number doesn’t fit into 32 bits, then the constraints cannot be satisfied. Hence, the circuit below ensures that in is $2^{32}-1$ or less.

include "circomlib/comparators.circom";

// 8 bit range check
template RangeCheck() {
  signal input in;
  component n2b = Num2Bits(32);
  n2b.in <== in;
}

component main = RangeCheck();

// if in = 2**32 - 1, it will accept
// if in = 2**32 it will reject

It is not necessary to constrain the outputs of Num2Bits like with LessThan, because internally, it already constraints out to be zero or one, and also constrains the binary representation to equal the input (via lc1 === in) as can be seen in the Num2Bits template below:

template Num2Bits(n) {
    signal input in;
    signal output out[n];
    var lc1=0;

    var e2=1;
    for (var i = 0; i<n; i++) {
        out[i] <-- (in >> i) & 1;
        out[i] * (out[i] -1 ) === 0; // CONSTRAINT HAPPENS HERE
        lc1 += out[i] * e2;
        e2 = e2+e2;
    }

    lc1 === in;
}

32-Bit Addition

Suppose we want to add two field elements x and y together, which represent 32-bit numbers.

The naïve implementation of 32-bit addition is to turn the field element into 32-bits, then build an “addition circuit” that adds each bit and carries the overflow. However, this creates a larger circuit than necessary.

Instead, we can do the following:

1. Range check x and y using the strategy outlined above
2. Add x and y together as field elements, i.e., z <== x + y
3. Convert z to a 33-bit number
4. Convert the least significant 32 bits of the 33-bit number to a field element.

This can be visualized as follows:

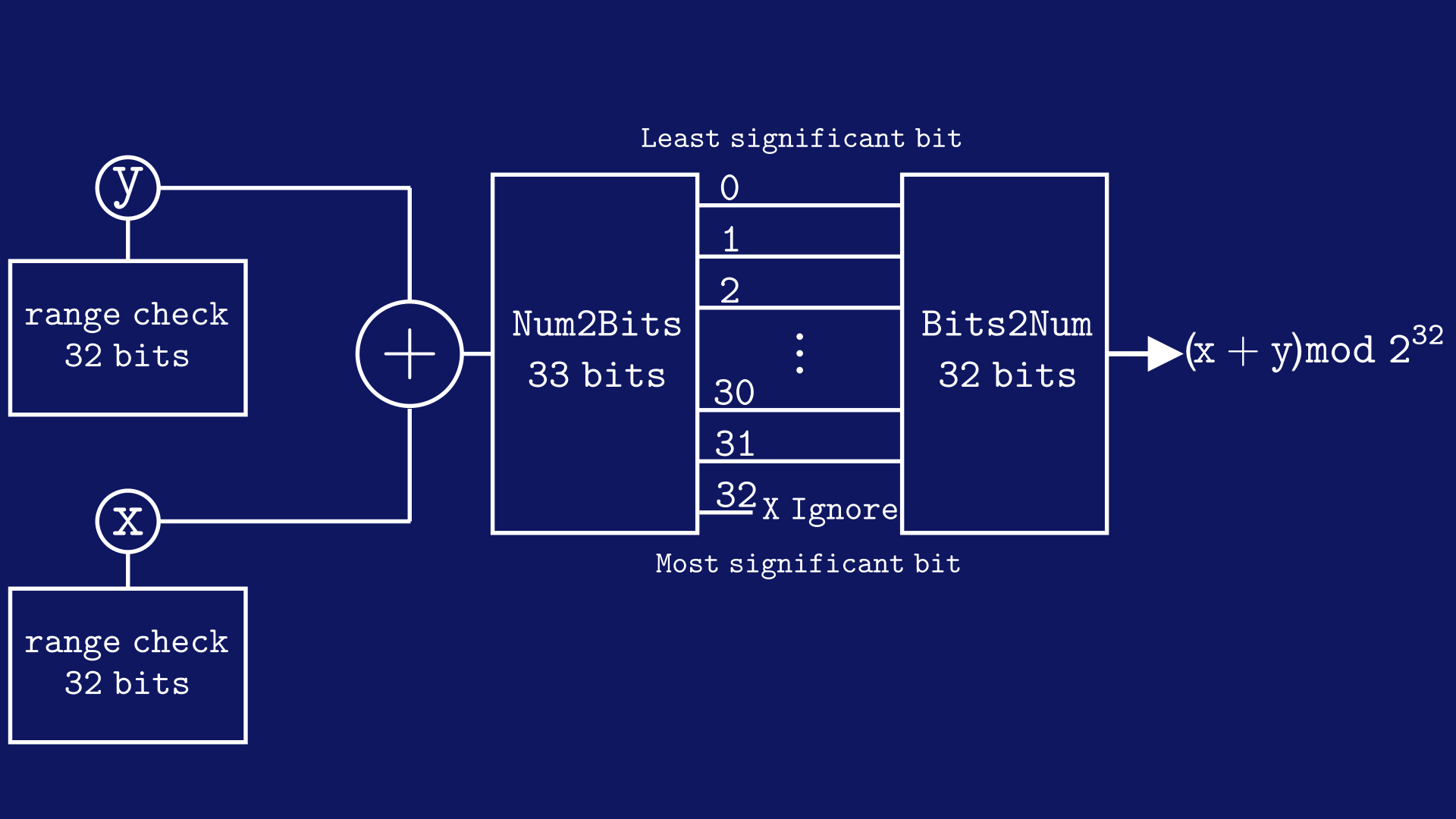
The most that x + y can overflow to is a 33-bit number. Consider that the maximum value x and y can hold is $2^{32}-1$. If we add that value to itself, we get

$$ \begin{align*} &(2^{32}-1)+(2^{32}-1)\\ &=2\cdot(2^{32}-1)\\ &=2^{33}-2 \end{align*} $$

The final number needs 33 bits to hold. (Recall that the maximum number 33 bits can hold is $2^{33} – 1$. Hence, the above number is the second largest number that 33 bits can hold.) Thus, we only need 33 bits to hold the sum before we remove the 33rd bit.

Below is the code for emulating and verifying 32-bit addition using Circom:

include "circomlib/comparators.circom";
include "circomlib/bitify.circom";

template Add32(n) {
  signal input x;
  signal input y;
  signal output out;

  // range check x and y
  component rCheckX = Num2Bits(32);
  component rCheckY = Num2Bits(32);
  rCheckX.in <== x;
  rCheckY.in <== y;

  // convert the sum to 33 bits
  component n2b33 = Num2Bits(33);
  n2b33.in <== x + y;

  // convert the least significant 32 bits
  // to the final result
  component b2n = Bits2Num(32);
  for (var i = 0; i < 32; i++) {
    b2n.in[i] <== n2b33.out[i];
  }

  b2n.out ==> out;
}

32-Bit Multiplication

The logic for 32-bit multiplication is extremely similar to 32-bit addition, except that we need to allow for the 32-bit multiplication to temporarily require up to 64 bits before only saving the final 32 bits:

$$ \begin{align*} &=(2^{32}-1)(2^{32}-1)\\ &=2^{64}-2^{32}-2^{32}+2\\ &=2^{64}-2^{33}+2 \end{align*} $$

The final number needs 64 bits to hold.

The implementation of this circuit is left as an exercise for the reader.

32-Bit Division and Modulo

Integer division is one of the most problematic bugs in ZK, as properly constraining it is much harder than the examples of addition and multiplication. Here are some examples of underconstrained division in the wild:

• https://code4rena.com/reports/2023-10-zksync#h-01-missing-range-constraint-on-remainder-check-in-div-opcode-implementation
• https://github.com/succinctlabs/sp1/issues/746

In integer division, the relationship between the numerator, denominator, quotient, and remainder is:

$$ \text{numerator}=\text{denominator}\times\text{quotient}+\text{remainder} $$

However, that constraint alone is not sufficient to ensure that the division was conducted properly.

For example, suppose we are trying to prove that we computed 12 / 7 = 1. Our circuit would have the values

$$ 12 = 7 \times 1 +5 $$

However, the following witness also satisfies the constraint:

$$ 12 = 7 \times 0 + 12 $$

We can guard against this by adding a constraint that the remainder is strictly less than the denominator.

Furthermore, we should be aware of the following potential bugs:

• This is not a concern for 32 bits in a 254-bit field (which is the default Circom uses), but we want to be sure the calculation $\text{denominator}\times\text{quotient}$ cannot overflow the underlying finite field.
• More generally, we do not want the computation $\text{denominator}\times\text{quotient}+\text{remainder}$ to overflow. If denominator and quotient are range-checked to 32 bits, then the most amount of bits the product $\text{denominator}\times\text{quotient}$ can hold is 64 bits, and if remainder is range-checked to 32 bits, the most amount of bits $\text{denominator}\times\text{quotient}+\text{remainder}$ can require is 65 bits. Therfore, working with a VM bit size of 32 bits is not a concern for the default field of Circom, but for other VM bit sizes, such as 128 bits, an overflow is possible.
• Division by zero can have unexpected behavior depending on which ZKVM you’re considering. The EVM for example does not panic when division by zero happens for example, but returns zero instead. In the RISC-V architecture, division by zero returns a word with all the bits set to 1.

It is impractical to directly compute integer division using only addition and multiplication (efficient algorithms like Karatsuba’s method for multiplication or efficient integer division use for-loops or recursion, which don’t map nicely to addition and multiplication), so it is better to compute the integer division result outside of the constraints.

In Circom, the / operator refers to modular division (multiplication by the multiplicative inverse) and the \ operator refers to integer division. The following code shows how to prove we calculated the quotient and remainder correctly. We include the computation of the remainder since we get it for free when proving we computed integer division properly.

include "circomlib/comparators.circom";
include "circomlib/bitify.circom";

template DivMod(wordSize) {
  // a wordSize over this could overflow 252
  assert(wordSize < 125);

  signal input numerator;
  signal input denominator;

  signal output quotient;
  signal output remainder;

  quotient <-- numerator \ denominator;
  remainder <-- numerator % denominator;

  // quotient and remainder still need
  // to be range checked because the
  // prover can supply any value

  // range check all the signals
  component n2bN = Num2Bits(wordSize);
  component n2bD = Num2Bits(wordSize);
  component n2bQ = Num2Bits(wordSize);
  component n2bR = Num2Bits(wordSize);
  n2bN.in <== numerator;
  n2bD.in <== denominator;
  n2bQ.in <== quotient;
  n2bR.in <== remainder;

  // core constraint
  numerator === quotient * denominator  + remainder;

  // remainder must be less than the denominator
  signal remLtDen;

  // depending on the application, we might be able
  // to use fewer than 252 bits
  remLtDen <== LessThan(wordSize)([remainder, denominator]);
  remLtDen === 1;

  // denominator is not zero
  signal isZero;
  isZero <== IsZero()(denominator);
  isZero === 0;
}

component main = DivMod(32);

32-Bit Bitshift

Suppose we wish to emulate the following code:

uint32 x;
uint32 s;
x << s;

A left-shift by s is equivalent to multiplying by $2^s$ where $s$ is the size of the shift, and a right-shift by s is equivalent to division by $2^s$. As seen in the previous chapter, the computation of powers can create a fairly large set of constraints. Therefore, it is generally more efficient to precompute every power of 2 up to the word size minus 1. Thus, for a left shift of a 32-bit number, we precompute every power of 2 up to 31 (word size (32) – 1): 1, 2, 4, 8, …, $2^{31}$ and multiply x by the appropriate selection using the conditional selection techniques discussed earlier. If the shift amount is 32 or greater, we multiply by zero.

The implementation is left as an exercise for the reader.

32-Bit AND, NOT, OR, XOR, and NOT

The Circomlib gates library has implementations for each of these circuits and they are self-explanatory, so we encourage the reader to simply read the code there. We show templates below on how to emulate the operation for the following:

Bitwise AND

uint32 a;
uint32 b;
a & b;

Bitwise NOT

uint32 x;
~x; // flip all the bits

Below is the code for computing and constraining the bitwise AND of a and b.

include "circomlib/gates.circom";
include "circomlib/bitify.circom";

template BitwiseAnd32() {
  signal input a;
  signal input b;
  signal output out;

  // range check
  component n2ba = Num2Bits(32);
  component n2bb = Num2Bits(32);
  n2ba.in <== a;
  n2bb.in <== b;

  component b2n = Bits2Num(32);
  component Ands[32];
  for (var i = 0; i < 32; i++) {
    Ands[i] = AND();
    Ands[i].a <== n2ba.out[i];
    Ands[i].b <== n2bb.out[i];
    Ands[i].out ==> b2n.in[i];
  }

  b2n.out ==> out;
}

component main = BitwiseAnd32();

The remaining operations for NOT, OR, and XOR are left as an exercise for the reader.

How ZK EVMs handle 256-bit numbers

The default Circom field cannot hold 256-bit numbers. Instead, each word in the EVM must be modeled with a list of smaller word sizes, similar to how a 64-bit computer can emulate the EVM.

For example, a 256-bit number can be modeled with four 64-bit words. When adding, we carry the overflow from the less significant words to the next significant word. If the most significant word overflows, we simply discard the overflow.

Appendix A: Proofs of Equivalence

We used the Certora prover to demonstrate equivalence of the following functions:

contract DemoMod32 {
    function mod32(uint256 x) public pure returns (uint256) {
        return x % (2**32);
    }

    function mod32e(uint256 x) public pure returns (uint256) {
        // only keep the 32 least significant bits
        return uint256(uint32(x)); 
    }
}

Here is the Certora verification language rule:

methods {
  function mod32(uint256) external returns (uint256) envfree;
  function mod32e(uint256) external returns (uint256) envfree;
}

rule test_Mod32AndMod32E_Equivalence() {
  uint256 x;
  assert mod32(x) == mod32e(x);
}

Here is the Certora report:

https://prover.certora.com/output/541734/6cd3303cb5f5441e8773adb5c79787d7?anonymousKey=0b945ee1440cd67efed3efba3162b0f924e8cf8f