In the previous chapter, we saw how unconstrained ghost variables can lead to false positives. We also learned how a require statement can be used to effectively constrain ghost values within rules.

However, while require works well for rules, this approach cannot be used for invariant verification. In this chapter, we’ll explore why the require statement is incompatible with invariants, and introduce axioms as the proper technique for safely constraining the values of ghost variables in invariants.

Understanding the Problem

To understand how an unconstrained ghost variable can affect invariant verification, consider the Voting contract shown below. This contract allows users to vote either in favor or against a proposal using the inFavor() or against() functions.

Copy
// SPDX-License-Identifier: MIT
pragma solidity 0.8.25;

/// @title A simple voting contract
contract Voting {

    // `hasVoted[user]` is true if the user voted.
    mapping(address => bool) public hasVoted;

    // keep the count of votes in favor
    uint256 public votesInFavor;

    // keep the count of votes against
    uint256 public votesAgainst; 


    // @notice Allows a user to vote in favor of the proposal.
    function inFavor() external {
        // Ensure the user has not already voted
        require(!hasVoted[msg.sender], "You have already voted.");
        hasVoted[msg.sender] = true;

        votesInFavor += 1;
    }

    /// @notice Allows a user to vote against the proposal.
    function against() external {
        // Ensure the user has not already voted
        require(!hasVoted[msg.sender], "You have already voted.");
        hasVoted[msg.sender] = true;

        votesAgainst += 1;
  }
}

This contract maintains three public state variables:

• hasVoted tracks whether a given user has already voted.
• votesInFavor and votesAgainst keep track of the number of votes in favor and against, respectively.

Now consider the specification below, which defines an invariant totalVotesSum and introduces a ghost variable totalVotes that tracks the total number of votes cast — a value that the contract itself does not record.

Copy
methods 
{
    function votesInFavor() external returns(uint256) envfree;
    function votesAgainst() external returns(uint256) envfree;
}

ghost mathint totalVotes;


hook Sstore hasVoted[KEY address voter] bool newStatus(bool oldStatus) {
    totalVotes = totalVotes + 1;
}

invariant totalVotesSum()
    totalVotes == votesInFavor() + votesAgainst();

Here is the detailed explanation of the above spec:

• The methods block declares the two public view functions, votesInFavor() and votesAgainst(), that we want to reference in the invariant. They are marked as envfree because their execution does not depend on environment variables like msg.sender, msg.value, etc.
• The ghost variable totalVotes is defined to count the number of users who have voted. Since the contract doesn’t expose this value directly, we simulate it using a ghost.
• The hook is attached to the Sstore operation of the hasVoted mapping. This hook gets triggered every time a value in the hasVoted mapping is updated, which only happens when a user casts a vote. In the hook, we increment totalVotes by 1—effectively counting every new voter regardless of whether they voted in favor or against.
• The invariant totalVotesSum asserts that the number of votes tracked by the ghost (totalVotes) must always match the actual sum of votes retrieved from the contract (votesInFavor + votesAgainst).

Once you place the above spec in your project directory, run the verification process using the certoraRun command. Next, open the verification result link shown in your terminal to view the result, which should look similar to the image below.

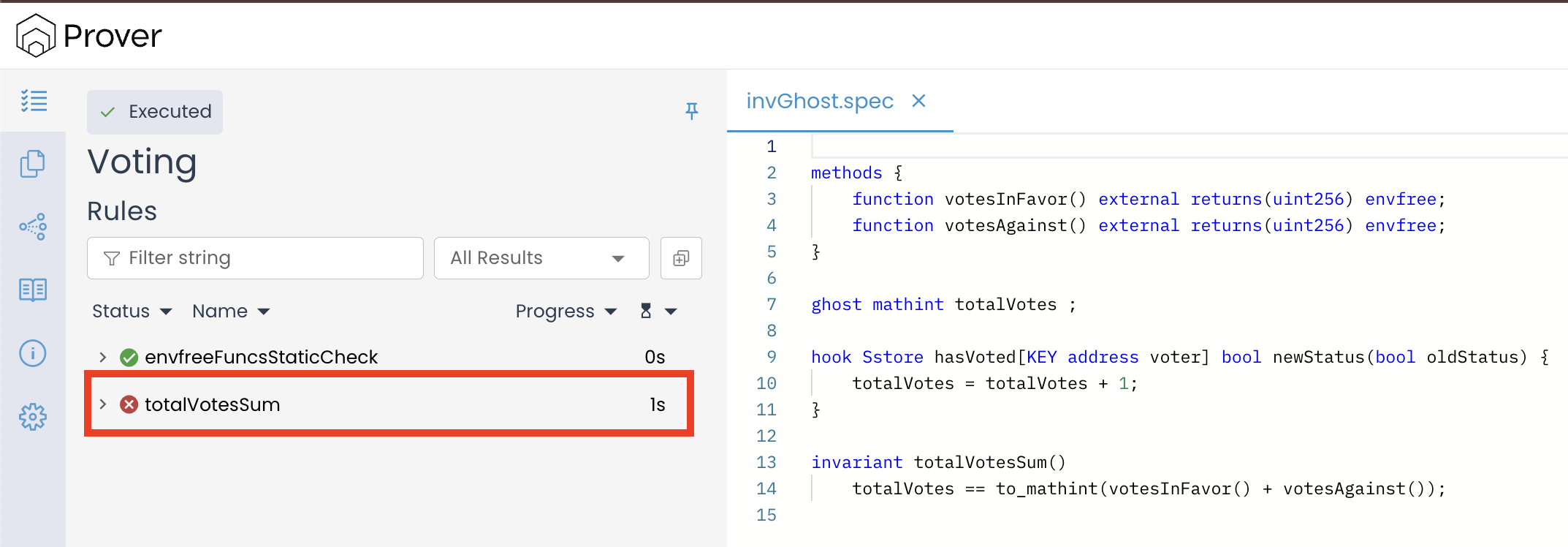
We can see that the Prover has failed to verify our invariant. Let’s explore why this happened and how we can address it.

Understanding the Cause of Violation

An invariant check involves two steps: the base case (checking the initial state after the constructor) and the inductive step (checking all subsequent state transitions).

In our situation, the Prover fails at the base case, meaning it cannot confirm that the invariant is valid right from the contract’s initial state.

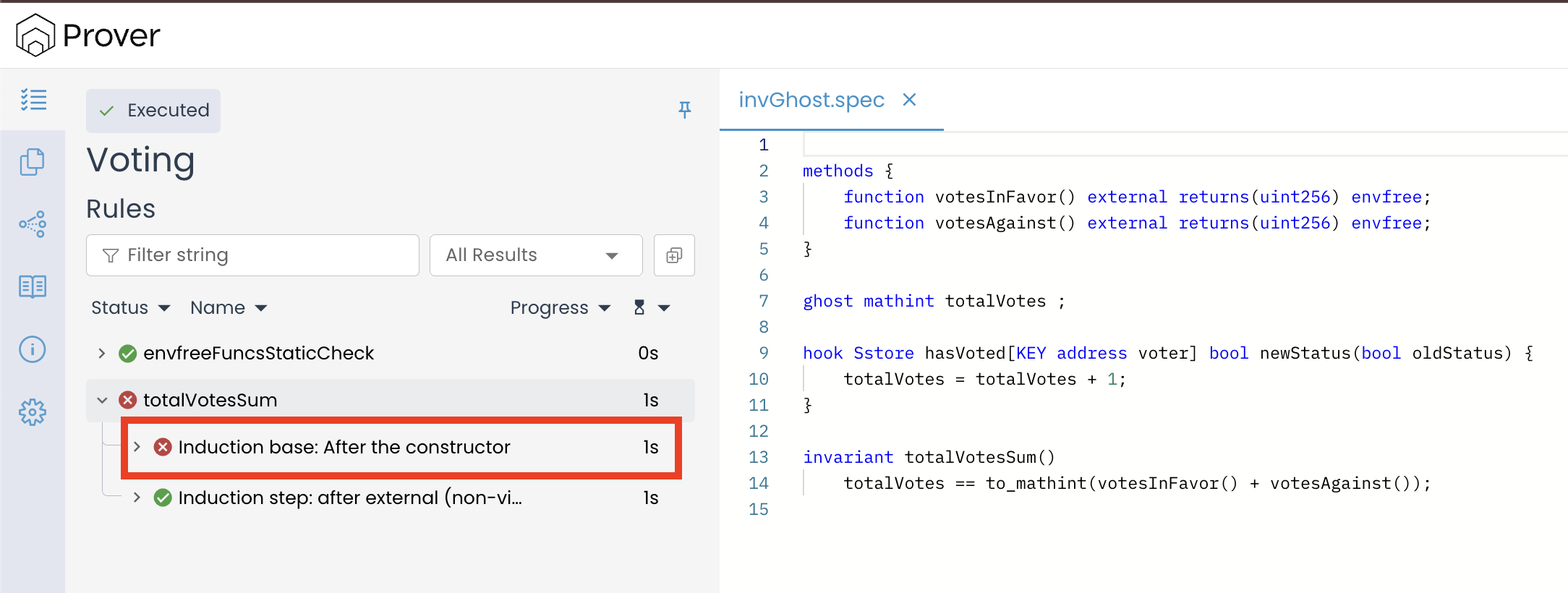
Our invariant fails at the base case because while verifying any invariant, the Prover must check the invariant in the contract’s initial state. However, since we never specified an initial value for totalVotes, the Prover adversarially chose one for us. In the call trace, we can see it chose -2.

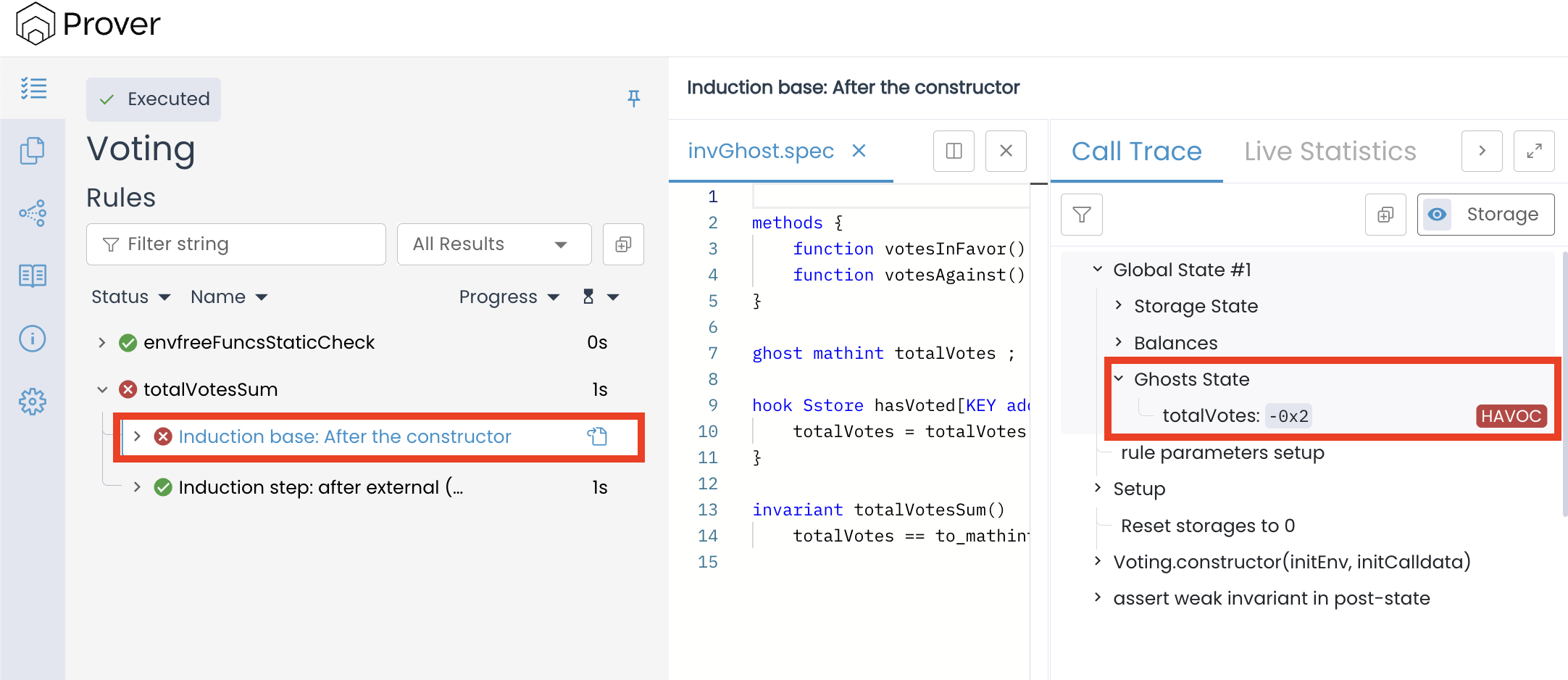
This causes the invariant totalVotes == votesInFavor() + votesAgainst() to immediately fail, as the Prover checks if -2 == 0 + 0, which is false. To fix this, we need to set the ghost’s initial value to 0. However, unlike in rules, we cannot use a require statement to constrain the ghost’s initial value. This doesn’t mean require has no place in invariants. It can be used inside a preserved block.

A preserved block is a special construct in CVL that lets you add extra assumptions while verifying an invariant. We will learn more about preserved blocks in a separate chapter.

Before we explore how to constrain ghost variables within invariants, let’s first understand why require cannot be used in this context.

Why We Can’t Use the require Statement?

In CVL, a require statement is used within a rule to act as a precondition. It tells the Prover, “Only check the following assertions for scenarios where these specific conditions hold.” This helps filter the execution paths or input combinations the Prover explores when evaluating the rule.

However, an invariant is very different. An invariant must hold in every possible state of the contract, including the initial one, without relying on any precondition. In other words, invariants express unconditional truths about the system.

Using a require statement inside an invariant doesn’t make sense, because require only limits paths during rule execution — it doesn’t define what is true before verification starts. What we need instead is a way to establish the initial state assumptions for the Prover.

To establish such initial truths — like setting a ghost variable’s starting value — we need a different construct: axioms.

Introduction to “Axioms”

Since invariants cannot rely on preconditions, we need a way to define what the Prover should assume about the system before verification begins. This is where axioms come in.

In CVL, an axiom allows us to declare a fact or relationship that the Prover must always accept as true. Instead of filtering the state space like require does, an axiom shapes the Prover’s reasoning by specifying the truths that hold in its logical universe.

In simple terms:

• A require statement limits what the Prover checks (it filters states).
• An axiom defines what the Prover believes (it establishes truths).

By using axioms, we can precisely control how ghost variables behave during invariant verification. For example, we can instruct the Prover to assume that a ghost variable starts at a certain value before the constructor, or that it always satisfies a given condition across all states.

There are two primary kinds of axioms used for ghost variables in CVL:

1. Initial State Axioms
2. Global Axioms

What are “Initial State Axioms”

An initial state axiom defines a property that the prover must assume to hold in the base step of invariant checking or right before the contract’s constructor executes.

In other words, it tells the Prover, “assume this condition is true when the contract is first deployed.” This allows you to control the initial values of ghost variables and eliminate the arbitrary starting states that can otherwise cause invariant failures.

The initial state axiom is declared using the init_state keyword, followed by the axiom keyword, and then the condition that defines the initial state of the ghost variable, as shown below:

Copy
ghost type_of_ghost name_of_ghost {
    init_state axiom boolean_expression;
}

For example, the code below defines a ghost variable sum_of_balances of type mathint and specifies that its value should be 0 before the contract’s constructor runs.

Copy
ghost mathint sum_of_balances {
    init_state axiom sum_of_balances == 0;
}

This will make sure that the Prover begins verification with the assumption that sum_of_balances starts at zero, preventing it from being treated as an arbitrary value in the initial state.

What are “Global Axioms”

While initial state axioms apply only to the contract’s first state, global axioms define properties that must hold in every state throughout verification.

A global axiom allows you to express universal truths about ghost variables — conditions that remain consistent across all possible contract executions. Once defined, the Prover accepts these statements as facts that are always valid and never need to be re-proven.

A global ghost axiom is defined by including the axiom keyword inside the ghost variable declaration block, followed by a condition that should hold in all program states, as shown below:

Copy
ghost type_of_ghost name_of_ghost {    
  axiom boolean_expression;
}

For example, the code below defines a ghost variable x of type mathint and asserts that its value is always greater than zero in every state throughout the verification process:

Copy
ghost mathint x {    
  axiom x > 0;
}

This means that during verification, the Prover will assume the condition $x > 0$ holds in all states, effectively constraining the ghost variable to never take zero or negative values.

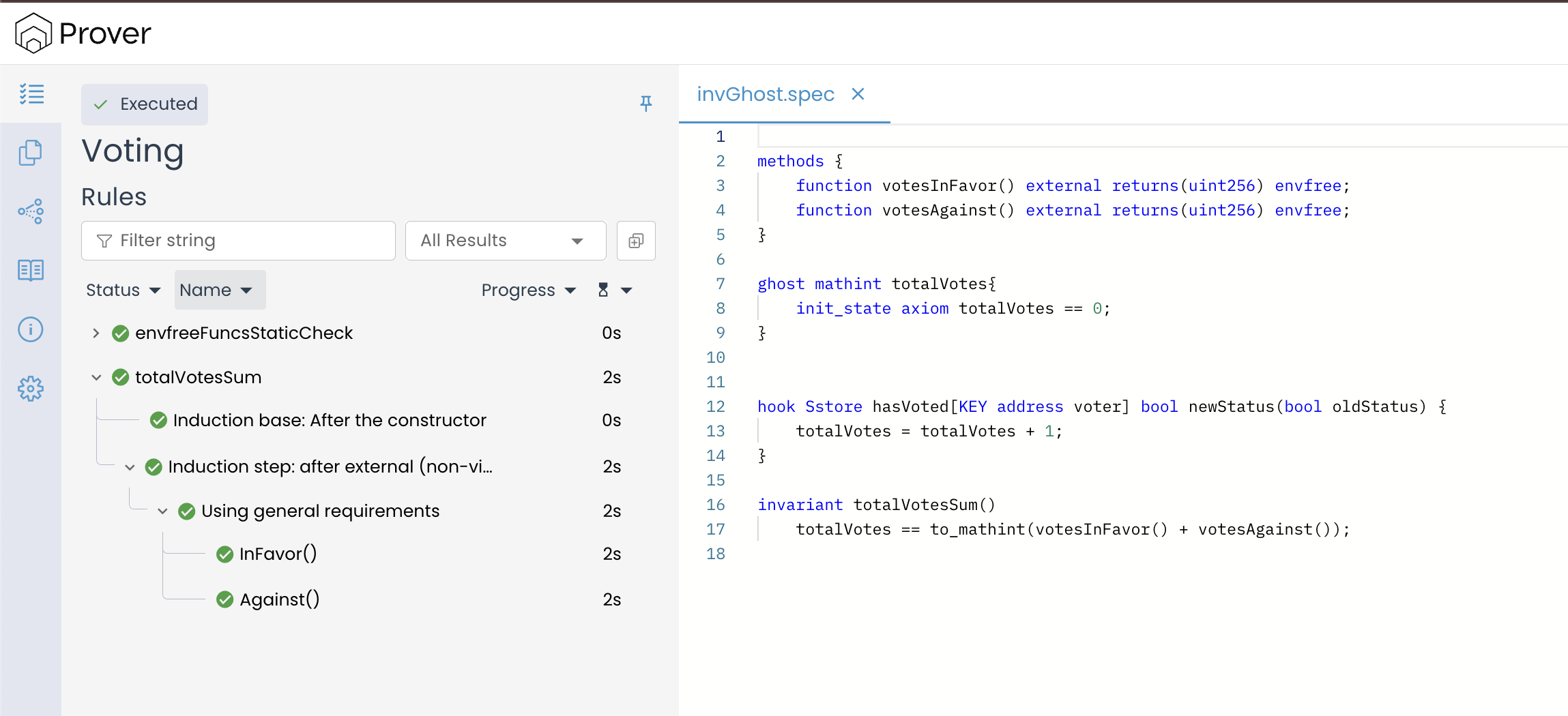
Using init_state Axiom in our Spec

Now that we understand the purpose of an init_state axiom, let’s apply it to the example we explored earlier, where our invariant failed because the ghost variable totalVotes started with an arbitrary value.

To fix this, we need to tell the Prover that totalVotes should begin at 0 immediately before the constructor runs. We do this by updating the ghost declaration to include an init_state axiom, as shown below:

Copy
ghost mathint totalVotes {    
  init_state axiom totalVotes == 0;
}

Once you have updated the spec to include the init_state axiom as shown above, re-run the Prover and open the verification result. Our new verification result should look similar to the result below.

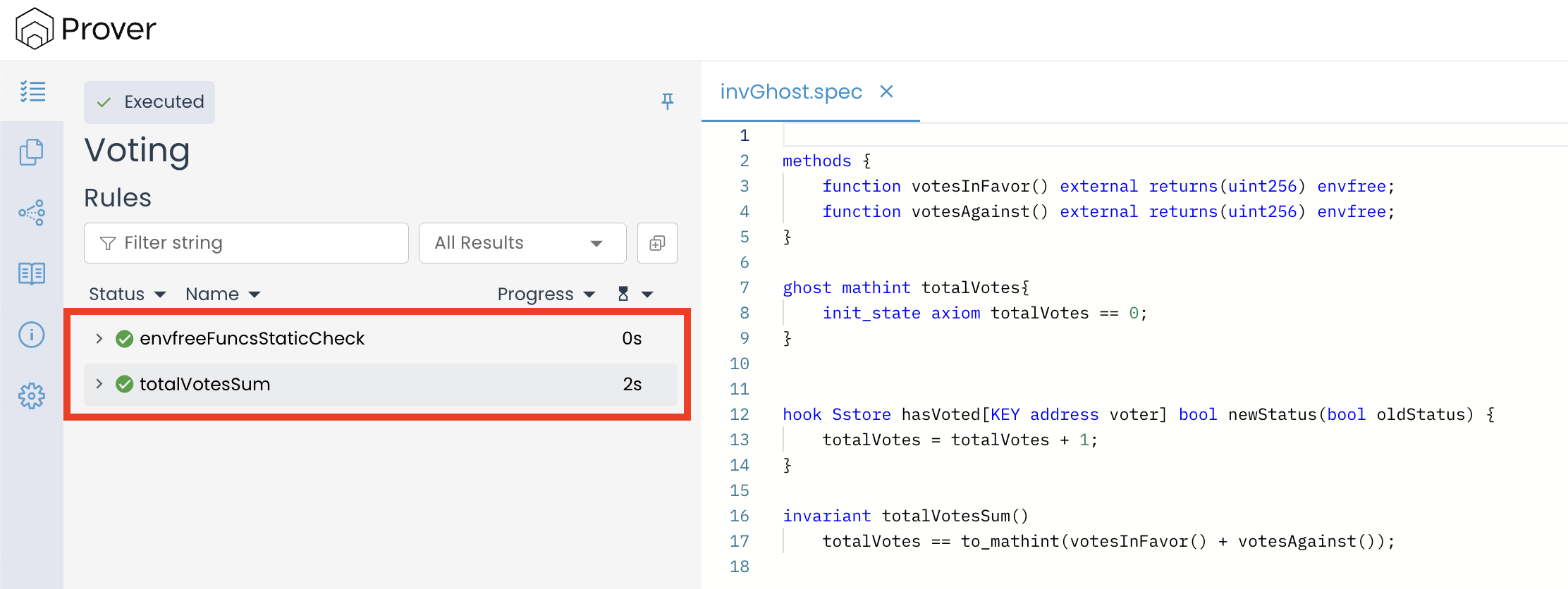
This time, we can observe that the Prover has successfully verified our invariant by passing both the base case and the inductive step, confirming that the total number of votes is always equal to the sum of votes cast in favor and votes cast against.

Using Global Axiom In Practice

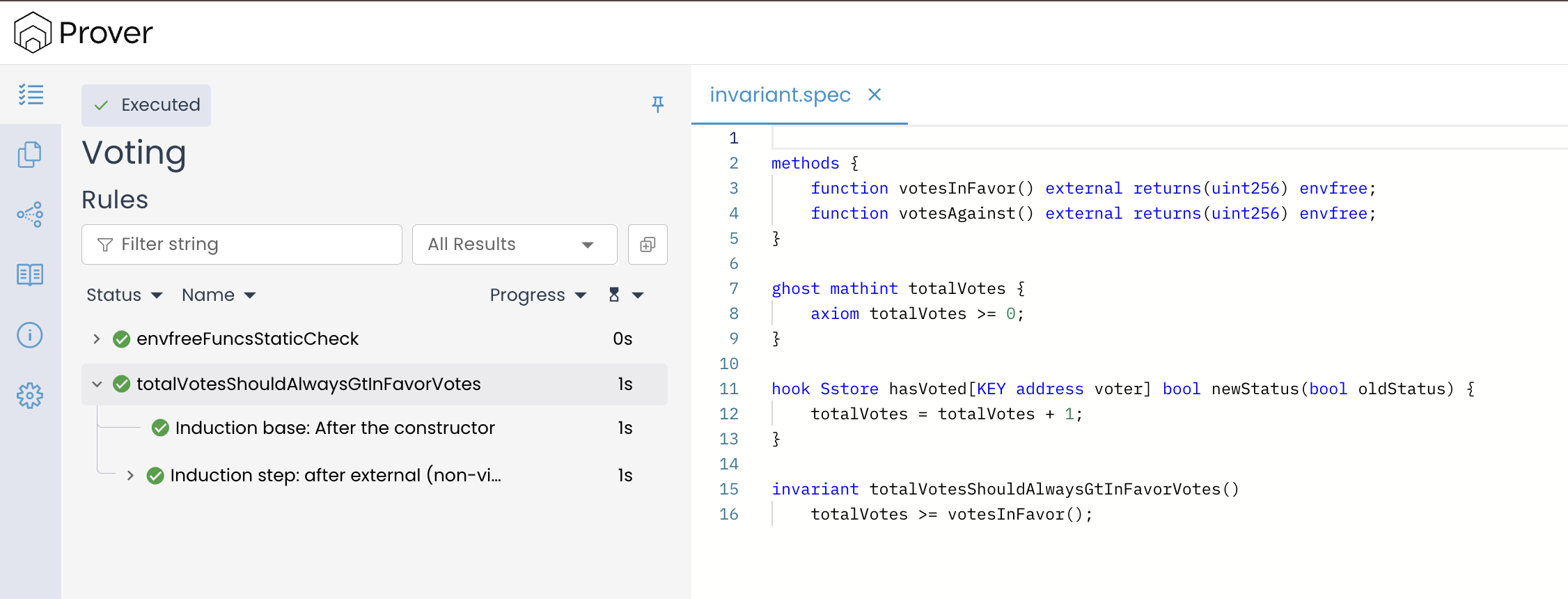
To understand how global axioms work in practice, consider the specification below:

Copy
methods {
    function votesInFavor() external returns(uint256) envfree;
    function votesAgainst() external returns(uint256) envfree;
}

ghost mathint totalVotes {
    axiom totalVotes >= 0;
}

hook Sstore hasVoted[KEY address voter] bool newStatus(bool oldStatus) {
    totalVotes = totalVotes + 1;
}

invariant totalVotesShouldAlwaysGtInFavorVotes()
    totalVotes >= votesInFavor();

The above specification asserts that the total number of votes (totalVotes) must always be greater than or equal to the number of votes in favor (votesInFavor). In the above spec, the key part is the line axiom totalVotes >= 0 , which introduces a global axiom that instructs the Prover to always assume that totalVotes is non-negative in every program state. This means the Prover will never explore any execution path where totalVotes becomes negative.

When you submit this spec to the Prover, it successfully verifies the invariant, as shown in the result below:

As we know, when an invariant is submitted for verification, the Prover performs two essential checks to ensure its correctness:

1. Base Case: In this step, the Prover first checks whether the invariant holds immediately after the contract’s constructor executes. In our example, this means verifying that totalVotes >= votesInFavor() is true in the contract’s initial state. Immediately after deployment, votesInFavor() is 0, while the Prover assumes that totalVotes can be any non-negative value. Since any non-negative number satisfies the condition totalVotes >= votesInFavor(), the base case holds.
2. Inductive Step: Next, the Prover ensures that if the invariant holds before any function execution, it continues to hold afterward for all possible transitions. Here, each time a user casts a vote, the hasVoted mapping is updated and the hook increments totalVotes.
   • When a user votes in favor, both votesInFavor and totalVotes increase by one, preserving the inequality.
   • When a user votes against, only totalVotes increases, which still maintains the invariant.

Because both conditions hold, the Prover successfully verifies the invariant. This confirms that under the global assumption totalVotes >= 0, the relationship between totalVotes and votesInFavor remains valid across all possible contract states.

This is how a global axiom helps the Prover reason about properties that are universally true in every program state. By defining axiom totalVotes >= 0, we establish a logical fact that holds throughout verification, without needing to re-prove it after every state transition. In this case, the axiom captures an intuitive truth that the total number of votes can never be negative, and allows the Prover to verify the invariant efficiently and soundly.

Conclusion

In this chapter, we demonstrated how unconstrained ghost variables can cause invariant proofs to fail at the base case. Since using require for initialization is not valid within invariants, we introduced axioms as the correct alternative. Specifically, the init_state axiom resolves the initialization problem by defining valid starting values for ghosts, while global axioms express properties that remain true across all contract states.