Introduction

In this chapter, we formally verify Solmate’s ERC-20 implementation, which includes the following:

• Standard state-changing functions: transfer(), approve(), transferFrom()
• Standard view functions: totalSupply(), balanceOf(), allowance()
• Extended internal functions: _mint(), _burn()

Note that while Solmate’s ERC-20 implementation includes a permit() function, we intentionally leave it out because formally verifying cryptographic signatures is not yet covered in this series.

What makes Solmate’s ERC-20 token interesting is its use of unchecked blocks to save gas during modifications to total supply and balances. Since unchecked blocks bypass Solidity’s built-in overflow checks, formal verification is essential to mathematically prove that overflows cannot occur.

Here’s the simplified Solmate ERC-20 implementation, with only the permit() function removed:

Copy
// SPDX-License-Identifier: AGPL-3.0-only
pragma solidity >=0.8.0;

/// @notice Modern and gas efficient ERC20 + EIP-2612 implementation.
/// @author Solmate (https://github.com/transmissions11/solmate/blob/main/src/tokens/ERC20.sol)
/// @author Modified from Uniswap (https://github.com/Uniswap/uniswap-v2-core/blob/master/contracts/UniswapV2ERC20.sol)
/// @dev Do not manually set balances without updating totalSupply, as the sum of all user balances must not exceed it.
abstract contract ERC20 {
    /*//////////////////////////////////////////////////////////////
                                 EVENTS
    //////////////////////////////////////////////////////////////*/

    event Transfer(address indexed from, address indexed to, uint256 amount);

    event Approval(address indexed owner, address indexed spender, uint256 amount);

    /*//////////////////////////////////////////////////////////////
                            METADATA STORAGE
    //////////////////////////////////////////////////////////////*/

    string public name;

    string public symbol;

    uint8 public immutable decimals;

    /*//////////////////////////////////////////////////////////////
                              ERC20 STORAGE
    //////////////////////////////////////////////////////////////*/

    uint256 public totalSupply;

    mapping(address => uint256) public balanceOf;

    mapping(address => mapping(address => uint256)) public allowance;

    /*//////////////////////////////////////////////////////////////
                               CONSTRUCTOR
    //////////////////////////////////////////////////////////////*/

    constructor(
        string memory _name,
        string memory _symbol,
        uint8 _decimals
    ) {
        name = _name;
        symbol = _symbol;
        decimals = _decimals;
    }

    /*//////////////////////////////////////////////////////////////
                               ERC20 LOGIC
    //////////////////////////////////////////////////////////////*/

    function approve(address spender, uint256 amount) public virtual returns (bool) {
        allowance[msg.sender][spender] = amount;

        emit Approval(msg.sender, spender, amount);

        return true;
    }

    function transfer(address to, uint256 amount) public virtual returns (bool) {
        balanceOf[msg.sender] -= amount;

        // Cannot overflow because the sum of all user
        // balances can't exceed the max uint256 value.
        unchecked {
            balanceOf[to] += amount;
        }

        emit Transfer(msg.sender, to, amount);

        return true;
    }

    function transferFrom(
        address from,
        address to,
        uint256 amount
    ) public virtual returns (bool) {
        uint256 allowed = allowance[from][msg.sender]; // Saves gas for limited approvals.

        if (allowed != type(uint256).max) allowance[from][msg.sender] = allowed - amount;

        balanceOf[from] -= amount;

        // Cannot overflow because the sum of all user
        // balances can't exceed the max uint256 value.
        unchecked {
            balanceOf[to] += amount;
        }

        emit Transfer(from, to, amount);

        return true;
    }

    /*//////////////////////////////////////////////////////////////
                        INTERNAL MINT/BURN LOGIC
    //////////////////////////////////////////////////////////////*/

    function _mint(address to, uint256 amount) internal virtual {
        totalSupply += amount;

        // Cannot overflow because the sum of all user
        // balances can't exceed the max uint256 value.
        unchecked {
            balanceOf[to] += amount;
        }

        emit Transfer(address(0), to, amount);
    }

    function _burn(address from, uint256 amount) internal virtual {
        balanceOf[from] -= amount;

        // Cannot underflow because a user's balance
        // will never be larger than the total supply.
        unchecked {
            totalSupply -= amount;
        }

        emit Transfer(from, address(0), amount);
    }
}

The ERC-20 implementation above is an abstract contract, which requires an inheriting contract to make it concrete. We also need to expose _mint() and _burn() through external functions so the Prover can invoke them during verification. To address both requirements, we use a harness contract.

A harness contract inherits from the contract under verification to make internal functions accessible to the Prover by wrapping them as external functions. It can also define helper view or pure functions that provide state queries and utility computations to simplify rule and invariant logic.

For this specification, the harness is a minimal contract that inherits the abstract ERC-20 implementation to both provide a concrete contract and make its internal functions (_mint() and _burn()) accessible for verification.

Here’s the harness contract:

Copy
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.25; 

import "src/Solmate/ERC20.sol";

contract ERC20Harness is ERC20 {    
    constructor (
        string memory _name, 
        string memory _symbol, 
        uint8 _decimals
    ) ERC20(_name, _symbol, _decimals) {}
    
    /// Left without access controls; integrators are expected to implement their own.
    function mint(address _to, uint256 _amount) external {
        _mint(_to, _amount);
    }
	
    /// Left without access controls; integrators are expected to implement their own.
    function burn(address _from, uint256 _amount) external {
        _burn(_from, _amount);
    }
}

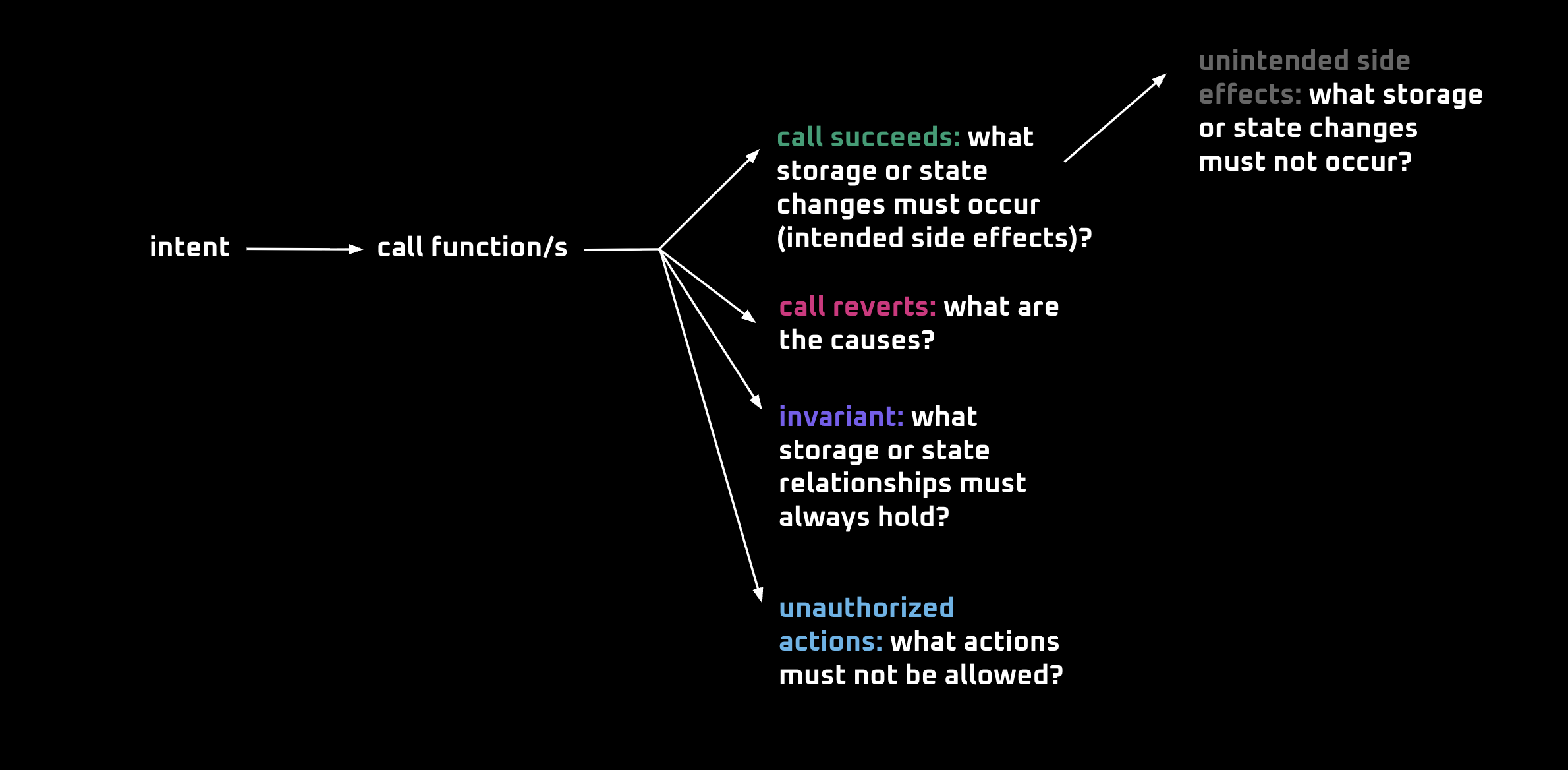
Sequenced approach to formally verifying ERC-20 properties

In this chapter, we take a sequenced approach to formally verify the ERC-20 contract’s properties. The outline is as follows:

• What is the intent? What does the user want to happen?
  • Which function(s) fulfill this intent?
    • If the call succeeds, how is the intended state change reflected?
    • If the call succeeds, what unintended side effects or state changes for uninvolved parties must not occur?
    • If the call reverts, what causes the revert?
• What invariants must always hold?
• What unauthorized actions (by functions or callers) must not be allowed?

The process is illustrated in the diagram below:

Then, we go through each step shown in the numbered sequence below:

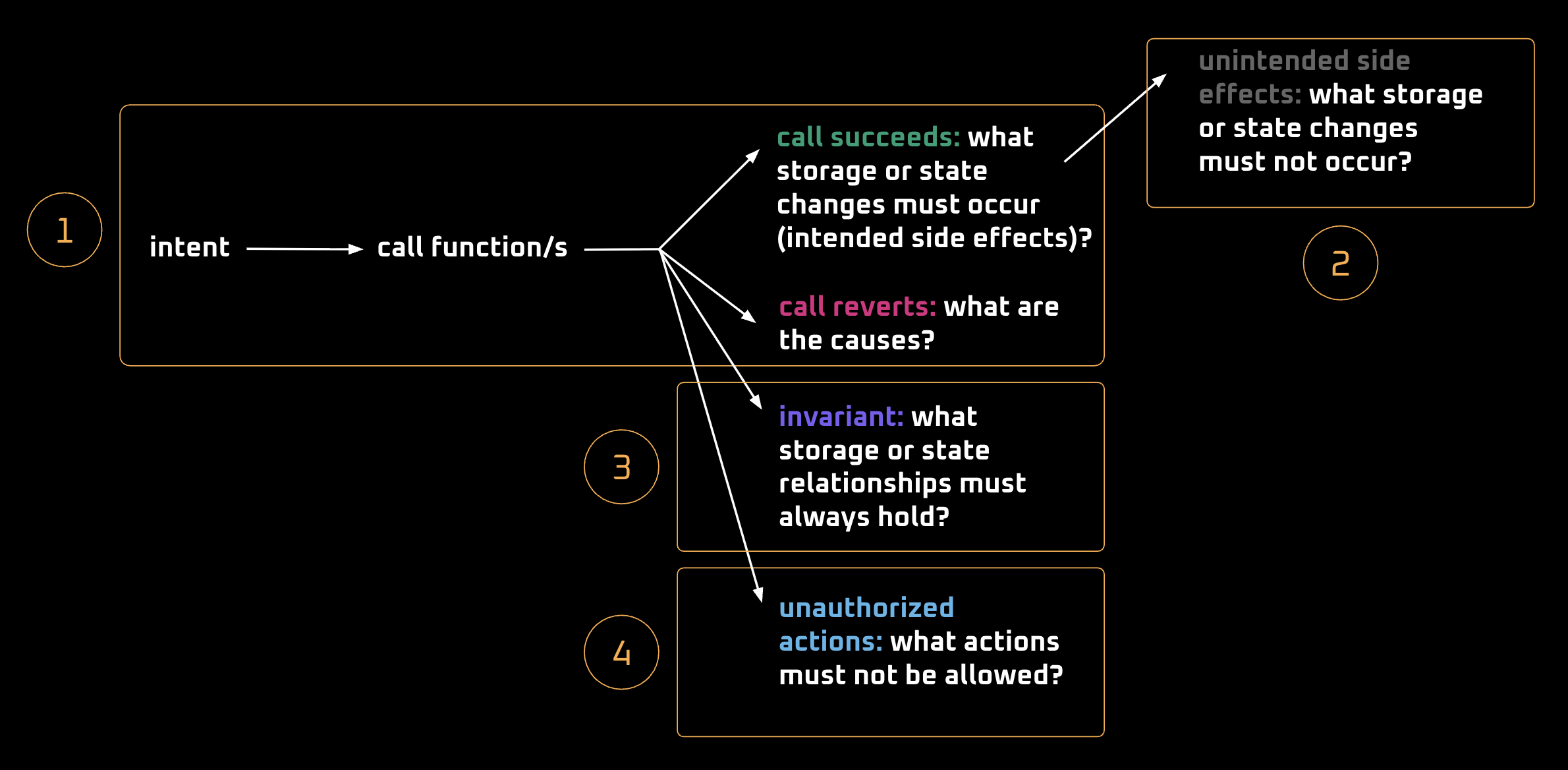
1. Verifying function correctness (calls succeed or revert)

transfer()

Let’s start with the intent of sending tokens — we verify that when a sender transfers tokens, the receiver receives the exact amount specified. This is achieved through the transfer() function.

Here’s the transfer() function implementation:

Copy
function transfer(address to, uint256 amount) public virtual returns (bool) {
    balanceOf[msg.sender] -= amount;

    // Cannot overflow because the sum of all user
    // balances can't exceed the max uint256 value.
    unchecked {
        balanceOf[to] += amount;
    }

    emit Transfer(msg.sender, to, amount);

    return true;
}

Here’s the CVL rule that verifies both the sender’s balance decreases and the receiver’s balance increases by the exact amount:

Copy
rule transfer_effectOnBalances(env e) {
    address receiver;
    uint256 amount;

    require balanceOf(e.msg.sender) + balanceOf(receiver) <= max_uint256; // will be replaced by an invariant
    
    mathint senderBalanceBefore = balanceOf(e.msg.sender);
    mathint receiverBalanceBefore = balanceOf(receiver);

    transfer(e, receiver, amount);

    mathint senderBalanceAfter = balanceOf(e.msg.sender);
    mathint receiverBalanceAfter = balanceOf(receiver);

    if (receiver != e.msg.sender) {
        assert senderBalanceAfter == senderBalanceBefore - amount;
        assert receiverBalanceAfter == receiverBalanceBefore + amount;
    } 
    else {
        assert senderBalanceAfter == senderBalanceBefore;
        assert receiverBalanceAfter == receiverBalanceBefore;
    }
}

Let’s explain this rule further.

The precondition restricts the Prover from assigning balances whose sum exceeds the max_uint256 limit as seen below:

Copy
require balanceOf(e.msg.sender) + balanceOf(receiver) <= max_uint256; // will be replaced by an invariant

This is necessary because the transfer() function uses an unchecked block when it adds the transfer amount to balanceOf[address], which causes the Prover to treat overflows as “possible” and report false positives.

However, because this precondition constrains values to max_uint256, the Prover cannot test overflow conditions that could actually occur, which can mask overflow bugs. Hence, it should be ruled out formally with a verified invariant, which we’ll address in the section "requireInvariant”.

After the precondition, we proceed with the following steps:

• Record the sender’s and receiver’s balances before the transfer() call.
• Invoke the transfer() call.
• Record the sender’s and receiver’s balances again after the call. We will use these values in the assertion to reason about the balance changes for both the sender and the receiver.

Copy
mathint senderBalanceBefore = balanceOf(e.msg.sender);
mathint receiverBalanceBefore = balanceOf(receiver);

transfer(e, receiver, amount);

mathint senderBalanceAfter = balanceOf(e.msg.sender);
mathint receiverBalanceAfter = balanceOf(receiver);

Now, the assertions:

• If the sender and receiver are different, we assert that:
  • The sender’s balance decreases by amount.
  • The receiver’s balance increases by amount.
• If the sender is the same as the receiver, we assert that the balances remain unchanged:

Copy
if (receiver != e.msg.sender) {
    assert senderBalanceAfter == senderBalanceBefore - amount;
    assert receiverBalanceAfter == receiverBalanceBefore + amount;
} 
else {
    assert senderBalanceAfter == senderBalanceBefore;
    assert receiverBalanceAfter == receiverBalanceBefore;
}

The assertion confirms direct value transfer with no deductions, as shown in this Prover run.

transfer() reverts

We just covered the successful transfer path. Next, we verify that transfer() reverts under failure conditions.

The following CVL rule accounts for all revert conditions in the assertions. It uses the biconditional operator (<=>) to state that a revert occurs if and only if one of the listed conditions is true. These conditions are:

• The sender does not have enough balance.
• ETH is sent along with a function call that is non-payable.

Copy
rule transfer_reverts(env e) {
    address receiver;
    uint256 amount;

    mathint senderBalance = balanceOf(e.msg.sender);

    transfer@withrevert(e, receiver, amount);
    bool isLastReverted = lastReverted;

    assert isLastReverted <=> (
        senderBalance < amount || // sender doesn't have enough balance
        e.msg.value != 0 // sending ETH with a call to transfer (non-payable)
    );
}

For this rule, we don’t define any preconditions, so we go straight to recording the state before the transfer call. The following line captures the value prior to the transfer call:

Copy
mathint senderBalance = balanceOf(e.msg.sender);

For the assertion, only two scenarios are listed as causes for reverting. The first is when the sender’s balance is less than the amount to transfer, since a sender should not be able to send more tokens than they own:

Copy
assert isLastReverted <=> (
    senderBalance < amount || // not enough balance
    e.msg.value != 0
);

The second case (e.msg.value != 0) results in a revert because the function is non-payable. Any nonzero msg.value causes it to fail. This is a revert condition for non-payable functions and will appear frequently during formal verification of the ERC-20.

The assertion uses a biconditional operator to guarantee that the function reverts if and only if either of the two cases occurs. This means no other condition should cause the function to revert. Here’s the Prover run.

transferFrom()

Here, we verify that when an authorized spender transfers tokens on behalf of a holder, the receiver receives the exact amount specified. This is done using the transferFrom() function as shown in the Solidity implementation below. The change in allowance from this transfer will be analyzed in a later section.

Copy
function transferFrom(
    address from,
    address to,
    uint256 amount
) public virtual returns (bool) {
    uint256 allowed = allowance[from][msg.sender]; // Saves gas for limited approvals.

    if (allowed != type(uint256).max) allowance[from][msg.sender] = allowed - amount;

    balanceOf[from] -= amount;

    // Cannot overflow because the sum of all user
    // balances can't exceed the max uint256 value.
    unchecked {
        balanceOf[to] += amount;
    }

    emit Transfer(from, to, amount);

    return true;
}

The following rule is nearly identical to transfer_effectOnBalances rule — the only difference is that it invokes transferFrom(). It does the following:

• Preconditions: Constrains the sum of holder and receiver balances to remain within max_uint256 to prevent the Prover from exploring overflow scenarios in the unchecked block.
• Pre-call and post-call states: Records balances of both accounts before and after the transferFrom() call so we can verify the exact balance changes in the assertions.
• Assertions:
  • If receiver != holder, assert that their balances differ by amount.
  • If receiver == holder, assert that the balance remains unchanged.

Copy
rule transferFrom_effectOnBalances(env e) {
    address holder;
    address receiver;
    uint256 amount;
    
    require balanceOf(holder) + balanceOf(receiver) <= max_uint256; // will be formally verified later

    mathint holderBalanceBefore = balanceOf(holder);
    mathint receiverBalanceBefore = balanceOf(receiver);

    transferFrom(e, holder, receiver, amount);

    mathint holderBalanceAfter = balanceOf(holder);
    mathint receiverBalanceAfter = balanceOf(receiver);

    if (receiver != holder) {
        assert holderBalanceAfter == holderBalanceBefore - amount;
        assert receiverBalanceAfter == receiverBalanceBefore + amount;
    } 
    else {
        assert holderBalanceAfter == holderBalanceBefore;
        assert receiverBalanceAfter == receiverBalanceBefore;
    }
}

View the Prover run.

transferFrom() reverts

The transferFrom()revert rule pattern is also similar to thetransfer() rule, except for an additional case involving the spender. As shown below, if the spender lacks sufficient allowance (that is, if spenderAllowance < amount), the transaction reverts:

Copy
rule transferFrom_reverts(env e) {
    address holder;
    address receiver;
    uint256 amount;

    mathint holderBalance = balanceOf(holder);
    mathint spenderAllowance = allowance(holder, e.msg.sender); 
 
 

    transferFrom@withrevert(e, holder, receiver, amount); // spender is the msg.sender
    bool isLastReverted = lastReverted;

    assert isLastReverted <=> (
        holderBalance < amount || 
        spenderAllowance < amount || 
        e.msg.value != 0 
    );
}

All other revert scenarios are the same as those in the transfer() rule. Here’s the Prover run.

Change in allowance

When a transferFrom() call succeeds, the holder’s approved allowance for the spender changes. The transferFrom() implementation includes this conditional:

Copy
if (allowed != type(uint256).max) allowance[from][msg.sender] = allowed - amount;

This means that if the current allowance is not set to the maximum uint256 value, the spent amount is deducted from it. If the allowance is set to the maximum, it behaves like an infinite allowance and remains unchanged.

This behavior is captured in the assertion section of the CVL rule shown below:

Copy
rule transferFrom_allowanceChange(env e) {
    address holder;
    address receiver;
    uint256 amount;

    mathint spenderAllowanceBefore = allowance(holder, e.msg.sender);

    transferFrom(e, holder, receiver, amount);
    mathint spenderAllowanceAfter = allowance(holder, e.msg.sender);

    if (spenderAllowanceBefore != max_uint256) {
        assert spenderAllowanceAfter == spenderAllowanceBefore - amount;
    }
    else {
        assert spenderAllowanceAfter == spenderAllowanceBefore;
    }
}

Prover run: link

approve()

Allowances are deducted within the transferFrom() function, but the actual allowance approval is set in the approve() function. Below is its implementation:

Copy
function approve(address spender, uint256 amount) public virtual returns (bool) {
    allowance[msg.sender][spender] = amount;

    emit Approval(msg.sender, spender, amount);

    return true;
}

The allowance variable is a public, nested mapping. Therefore, Solidity automatically generates a getter function, which allows it to be invoked directly in CVL (allowance(e.msg.sender, spender)):

Copy
rule approve_spenderAllowance(env e) {
    address spender;
    uint256 amount;

    approve@withrevert(e, spender, amount);
    bool isReverted = lastReverted;

    mathint approvedAmountAfter = allowance(e.msg.sender, spender);

    assert !isReverted => approvedAmountAfter == amount;
    assert isReverted <=> e.msg.value != 0;
}

Prover run: link

For conciseness, the rule above combines both the successful and reverting cases, using implication and the biconditional operator instead of creating separate rules for each or using an if/else block.

The approve() function must be invoked within the env e context because it depends on global environment variables such as msg.sender and msg.value. Specifically, the function uses msg.sender to determine which address is setting the allowance for the spender:

Copy
function approve(address spender, uint256 amount) public virtual returns (bool) {
    allowance[msg.sender][spender] = amount; // relies on msg.sender
    ...
}

Now for the assertion:

• If the function call succeeds, the allowance is set to the specified amount.
• The function reverts if and only if e.msg.value is nonzero, meaning ETH was sent with the approve function call.

Copy
assert !isReverted => approvedAmountAfter == amount;
assert isReverted <=> e.msg.value != 0;

transfer(), transferFrom() and approve() return true on a successful call

Other than their state-changing operations, transfer(), transferFrom(), and approve() must return true on successful execution, as required by the ERC-20 standard.

The following rules call their respective functions with @withrevert to capture whether they revert, store the result in isLastReverted, and assert that if the call did not revert, it must return true:

Copy
rule transfer_successReturnsTrue(env e) {
    address receiver;
    uint256 amount;

    bool retVal = transfer@withrevert(e, receiver, amount);
    bool isLastReverted = lastReverted;

    assert !isLastReverted => (retVal == true);
}

rule transferFrom_successReturnsTrue(env e) {
    address holder;
    address receiver;
    uint256 amount;

    bool retVal = transferFrom@withrevert(e, holder, receiver, amount);
    bool isLastReverted = lastReverted;

    assert !isLastReverted => (retVal == true);
}

rule approve_successReturnsTrue(env e) {
    address spender;
    uint256 amount;

    bool retVal = approve@withrevert(e, spender, amount);
    bool isReverted = lastReverted;
    
    assert !isReverted => (retVal == true);
}

Prover run: link

These rules verify that transfer(), transferFrom(), and approve() return true on successful calls.

mint()

Increasing the total supply is the intent of minting. At the same time, the newly minted tokens are assigned to a receiver, increasing their balance. The Solidity implementation below shows both totalSupply and balanceOf[to] being increased by amount:

Copy
function _mint(address to, uint256 amount) internal virtual {
    totalSupply += amount;

    // Cannot overflow because the sum of all user
    // balances can't exceed the max uint256 value.
    unchecked {
        balanceOf[to] += amount;
    }
    ...
}

The increase to balanceOf[address] occurs inside an unchecked block, while the increase to totalSupply happens outside the unchecked block and is protected by the Solidity compiler’s overflow checks.

Because of the unchecked block, the Prover explores the possibility of balance overflow, even though this cannot actually occur given that balances increase in step with totalSupply. To prevent false positives, we add the precondition require totalSupply() >= balanceOf(receiver).

Here’s the CVL rule that captures both the increase in total supply and the corresponding increase in the receiver’s balance:

Copy
rule mint_increasesTotalSupplyAndBalance() {
    address receiver;
    uint256 amount;

    require totalSupply() >= balanceOf(receiver); // will be replaced by an invariant

    mathint totalSupplyBefore = totalSupply();
    mathint receiverBalanceBefore = balanceOf(receiver);

    mint(receiver, amount);

    mathint totalSupplyAfter = totalSupply();
    mathint receiverBalanceAfter = balanceOf(receiver);

    assert totalSupplyAfter == totalSupplyBefore + amount;
    assert receiverBalanceAfter == receiverBalanceBefore + amount;
}

Prover run: link

Following the established pattern, we capture the state before and after the mint() method call:

Copy
mathint totalSupplyBefore = totalSupply();
mathint receiverBalanceBefore = balanceOf(receiver);

mint(receiver, amount);

mathint totalSupplyAfter = totalSupply();
mathint receiverBalanceAfter = balanceOf(receiver);

And now the assertion, where both the increase in total supply and the corresponding increase in the receiver’s balance equal the amount:

Copy
assert totalSupplyAfter == totalSupplyBefore + amount;
assert receiverBalanceAfter == receiverBalanceBefore + amount;

mint() reverts

The mint() function reverts if and only if the sum of the total supply and the mint amount exceeds max_uint256. This represents an overflow scenario. Here is the CVL rule that captures this behavior:

Copy
rule mint_reverts() {
    address receiver;
    uint256 amount;

    mathint totalSupply = totalSupply();

    mint@withrevert(receiver, amount);
    bool isReverted = lastReverted;

    assert isReverted <=> totalSupply + amount > max_uint256;
}

Prover run: link

burn()

While minting increases the total supply, the intent of burning is to reduce it. Each burn operation decreases both the total supply and the token owner’s balance.

Here’s the implementation:

Copy
function _burn(address from, uint256 amount) internal virtual {
    balanceOf[from] -= amount;

    // Cannot underflow because a user's balance
    // will never be larger than the total supply.
    unchecked {
        totalSupply -= amount;
    }

    emit Transfer(from, address(0), amount);
}

Here’s the rule that captures both the decrease in total supply and the decrease in the token owner’s balance:

Copy
rule burn_decreasesTotalSupplyAndBalance() {
    address holder;
    uint256 amount;
			
	require totalSupply() >= balanceOf(holder); // will be replaced by an invariant
		
    mathint holderBalanceBefore = balanceOf(holder);
    mathint totalSupplyBefore = totalSupply();

    burn(holder, amount);

    mathint holderBalanceAfter = balanceOf(holder);
    mathint totalSupplyAfter = totalSupply();

    assert holderBalanceAfter == holderBalanceBefore - amount;
    assert totalSupplyAfter == totalSupplyBefore - amount;
}

Prover run: link

In the _burn() function, the operation totalSupply -= amount is inside an unchecked block. Hence, the Prover explores the possibility of underflow, even though it cannot actually occur. To prevent this, we add the precondition require totalSupply() >= balanceOf(holder) in the rule.

For the rest of the code, the pattern is similar to mint(), except both the balance and total supply decrease by the specified amount, as expected when burning.

burn() reverts

The burn() function reverts if and only if the holder’s balance is less than the amount to burn. This is a Solidity-enforced safety check that triggers a revert when balanceOf[from] -= amount(executed outside an unchecked block) attempts to subtract more than the available balance.

Here’s the CVL rule that verifies this behavior:

Copy
rule burn_reverts(env e) {
	address holder;
	uint256 amount;

	mathint holderBalance = balanceOf(holder);

	burn@withrevert(holder, amount);
	bool isReverted = lastReverted;

	assert isReverted <=> holderBalance < amount;
}

Prover run: link

2. Unintended side effects of transfer, transferFrom, mint and burn

Having verified that functions behave correctly in both success and revert scenarios, we now verify that there are no unintended side effects or state changes for uninvolved parties.

A function can unintentionally cause changes in storage for accounts that are not involved in the operation. For this contract, we formally verify that no uninvolved account’s balance is modified by transfer(), transferFrom(), mint(), or burn().

Each rule follows the same pattern: we designate an address as uninvolved (through require statements), capture its balance before the operation, execute the function, then assert the balance remains unchanged. This proves that only accounts explicitly passed as arguments are affected:

Copy
rule noUninvolvedBalancesAreAffectedByDirectTransfer(env e) {
    address receiver;
    address other;
    uint256 amount;

    require other != receiver;
    require other != e.msg.sender;

    mathint otherBalanceBefore = balanceOf(other);
    transfer(e, receiver, amount);

    mathint otherBalanceAfter = balanceOf(other);
    assert otherBalanceAfter == otherBalanceBefore;
}

rule noUninvolvedBalancesAreAffectedByTransferFrom(env e) {
    address holder;
    address receiver;
    address other;
    uint256 amount;

    require other != receiver;
    require other != holder;

    mathint otherBalanceBefore = balanceOf(other);
    transferFrom(e, holder, receiver, amount);

    mathint otherBalanceAfter = balanceOf(other);
    assert otherBalanceAfter == otherBalanceBefore;
}

rule noUninvolvedBalancesAreAffectedByMint() {
    address account;
    address other;
    uint256 amount;

    require account != other;

    mathint otherBalanceBefore = balanceOf(other);
    mint(account, amount);

    mathint otherBalanceAfter = balanceOf(other);
    assert otherBalanceAfter == otherBalanceBefore;
}

rule noUninvolvedBalancesAreAffectedByBurn() {
    address account;
    address other;
    uint256 amount;

    require account != other;

    mathint otherBalanceBefore = balanceOf(other);
    burn(account, amount);

    mathint otherBalanceAfter = balanceOf(other);
    assert otherBalanceAfter == otherBalanceBefore;
}

Prover run: link

3. Invariants

Now that we’ve verified both the successful and reverting paths, and that no unintended side effects occur, we can move on to invariants — conditions that must always hold, regardless of which function is called, which arguments are used, or how many valid calls are made in sequence.

Sum of balances must equal the total supply

Under no circumstance should the sum of all balances differ from the total supply, because any divergence indicates that tokens have been created or destroyed outside of mint() or burn()— either giving users more tokens than actually exist or causing tokens to disappear from the system. The following CVL specification formally verifies this invariant:

Copy
ghost mathint g_sumOfBalances {
    init_state axiom g_sumOfBalances == 0;
}

hook Sstore balanceOf[KEY address account] uint256 newBalance (uint256 oldBalance) {
    g_sumOfBalances = g_sumOfBalances + newBalance - oldBalance;
}

hook Sload uint256 balance balanceOf[KEY address account] { 
    require g_sumOfBalances >= balance;
}

invariant totalSupplyEqualsSumOfBalances()
	to_mathint(totalSupply()) == g_sumOfBalances;

Prover run: link

Let’s discuss further.

The first block declares a ghost variable g_sumOfBalances as a mathint and initializes it to zero. Without this initialization, the Prover assigns arbitrary starting values, which could lead to false positive violations:

Copy
ghost mathint g_sumOfBalances {
    init_state axiom g_sumOfBalances == 0;
}

Now, here’s the Sstore hook where the ghost variable g_sumOfBalances is used to store and track changes in the total account balances:

Copy
hook Sstore balanceOf[KEY address account] uint256 newBalance (uint256 oldBalance) {
    g_sumOfBalances = g_sumOfBalances + newBalance - oldBalance;
}

The Sload hook below constrains balance reads to prevent the Prover from assigning values greater than the tracked sum of balances:

Copy
hook Sload uint256 balance balanceOf[KEY address account] { 
    require g_sumOfBalances >= balance;
}

Finally, we formally verify that the total supply equals the sum of all balances:

Copy
invariant totalSupplyEqualsSumOfBalances()
	to_mathint(totalSupply()) == g_sumOfBalances;

requireInvariant — invariant as a precondition

Not only is the invariant totalSupplyEqualsSumOfBalances useful as a universal property, but we also rely on it as a proven assumption in place of preconditions.

Beyond the obvious meaning that the total supply equals the sum of all balances, the invariant totalSupply() == g_sumOfBalances also implies:

• The total supply is always greater than or equal to any individual balance.
• Both the total supply and sum of balances remain within max_uint256.

Recall that the earlier transfer and transferFrom rules included a precondition requiring balances to remain within max_uint256. This could have hidden an overflow bug because the precondition assumed and constrained the balances, which may have unintentionally filtered out states where the bug could appear.

Therefore, using the verified invariant totalSupplyEqualsSumOfBalances as the precondition is safer, because it ensures that the rule is executed with a property that holds in “all” reachable states.

We now replace the require statements with requireInvariant totalSupplyEqualsSumOfBalances, as shown below:

Copy
rule transfer_effectOnBalances_requireInvariant(env e) {
    address receiver;
    uint256 amount;

    // previously: `require balanceOf(e.msg.sender) + balanceOf(receiver) <= max_uint256`
    requireInvariant totalSupplyEqualsSumOfBalances();
    
    mathint senderBalanceBefore = balanceOf(e.msg.sender);
    mathint receiverBalanceBefore = balanceOf(receiver);

    transfer(e, receiver, amount);

    mathint senderBalanceAfter = balanceOf(e.msg.sender);
    mathint receiverBalanceAfter = balanceOf(receiver);

    if (receiver != e.msg.sender) {
        assert senderBalanceAfter == senderBalanceBefore - amount;
        assert receiverBalanceAfter == receiverBalanceBefore + amount;
    } 
    else {
        assert senderBalanceAfter == senderBalanceBefore;
        assert receiverBalanceAfter == receiverBalanceBefore;
    }
}

rule transferFrom_effectOnBalances_requireInvariant(env e) {
    address holder;
    address receiver;
    uint256 amount;

    // previously: `require balanceOf(e.msg.sender) + balanceOf(receiver) <= max_uint256`
    requireInvariant totalSupplyEqualsSumOfBalances();

    mathint holderBalanceBefore = balanceOf(holder);
    mathint receiverBalanceBefore = balanceOf(receiver);

    transferFrom(e, holder, receiver, amount);

    mathint holderBalanceAfter = balanceOf(holder);
    mathint receiverBalanceAfter = balanceOf(receiver);

    if (receiver != holder) {
        assert holderBalanceAfter == holderBalanceBefore - amount;
        assert receiverBalanceAfter == receiverBalanceBefore + amount;
    } 
    else {
        assert holderBalanceAfter == holderBalanceBefore;
        assert receiverBalanceAfter == receiverBalanceBefore;
    }
}

Also, the burn and mint rules include a precondition requiring that the total supply be greater than or equal to the holder’s and receiver’s balances, respectively. This require precondition is an assumed constraint, and to be safe, we replace it with a proven invariant.

Since the invariant totalSupplyEqualsSumOfBalances also implies that the total supply is greater than or equal to all individual balances, we can replace the require precondition with requireInvariant totalSupplyEqualsSumOfBalances:

Copy
rule mint_increasesTotalSupplyAndBalance_requireInvariant() {
    address receiver;
    uint256 amount;

    // previously: `require totalSupply() >= balanceOf(receiver)`
    requireInvariant totalSupplyEqualsSumOfBalances();

    mathint totalSupplyBefore = totalSupply();
    mathint receiverBalanceBefore = balanceOf(receiver);

    mint(receiver, amount);

    mathint totalSupplyAfter = totalSupply();
    mathint receiverBalanceAfter = balanceOf(receiver);

    assert totalSupplyAfter == totalSupplyBefore + amount;
    assert receiverBalanceAfter == receiverBalanceBefore + amount;
}


rule burn_decreasesTotalSupplyAndBalance_requireInvariant() {

    address holder;
    uint256 amount;

    // previously: `require totalSupply() >= balanceOf(holder)`
    requireInvariant totalSupplyEqualsSumOfBalances(); 

    mathint holderBalanceBefore = balanceOf(holder);
    mathint totalSupplyBefore = totalSupply();

    burn(holder, amount);

    mathint holderBalanceAfter = balanceOf(holder);
    mathint totalSupplyAfter = totalSupply();

    assert holderBalanceAfter == holderBalanceBefore - amount;
    assert totalSupplyAfter == totalSupplyBefore - amount;
}

Prover run: link

4. Unauthorized actions — methods and callers not allowed to change state

This verifies that certain state changes or actions must not occur outside explicitly permitted functions or callers.

Only certain methods can change storage / state

Let’s begin with the property: “Only mint() and burn() can change the total supply.”

The rule below is a parametric rule (see chapter “Introduction to Parametric Rules”) where functions can be called arbitrarily (via f(e, args)), but only mint() and burn() are allowed to change the totalSupply. This is enforced by the assertion where totalSupplyAfter != totalSupplyBefore implies (=>) that only these two functions may cause such a change:

Copy
rule onlyMethodsCanChangeTotalSupply(env e, method f, calldataarg args) {
    mathint totalSupplyBefore = totalSupply();

    f(e, args);
    mathint totalSupplyAfter = totalSupply();

    assert totalSupplyAfter != totalSupplyBefore => (
        f.selector == sig:mint(address,uint256).selector ||
        f.selector == sig:burn(address,uint256).selector
    );
}

While this asserts which functions are allowed to modify totalSupply, it also implies that all other functions are unauthorized to do so.

The remaining rules in this category are shown below and follow the same pattern:

• Only mint(), burn(), transfer() and transferFrom() can change account balances:

  Copy
  rule onlyMethodsCanChangeAccountBalances(env e, method f, calldataarg args) {
      address account;
      mathint balanceBefore = balanceOf(account);
      
      f(e, args);
      mathint balanceAfter = balanceOf(account);
  
      assert balanceBefore != balanceAfter => (
          f.selector == sig:transfer(address,uint256).selector ||
          f.selector == sig:transferFrom(address,address,uint256).selector ||
          f.selector == sig:mint(address,uint256).selector ||
          f.selector == sig:burn(address,uint256).selector
      );
  }
  

• Only approve() and transferFrom()can change allowances:

  Copy
  rule onlyMethodsCanChangeAllowance(env e, method f, calldataarg args) {
      address holder;
      address spender;
  
      mathint allowanceBefore = allowance(holder, spender);
  
      f(e, args);
      mathint allowanceAfter = allowance(holder, spender);
  
      assert allowanceAfter != allowanceBefore => (
          f.selector == sig:approve(address,uint256).selector ||
          f.selector == sig:transferFrom(address,address,uint256).selector
      );
  }
  

Now that we have written the rules that verify which methods may modify the state, we can write the rule that verifies which callers are allowed to reduce a holder’s balance.

Only holders and spenders can reduce a holder’s balance

Another unauthorized action is reducing a balance when the caller is not the holder or an approved spender. The following rule verifies this property:

Copy
rule onlyHolderAndSpenderCanReduceHolderBalance(env e, method f, calldataarg args) filtered {
	// `burn()` is excluded since permission checks are left to the integrator / developer
    f -> f.selector != sig:burn(address,uint256).selector                                                   
} {
    requireInvariant totalSupplyEqualsSumOfBalances(); 

    address account;

    mathint spenderAllowanceBefore = allowance(account, e.msg.sender);
	mathint holderBalanceBefore = balanceOf(account);
    
    f(e, args);
	mathint holderBalanceAfter = balanceOf(account);

    assert (holderBalanceAfter < holderBalanceBefore) => (
        e.msg.sender == account ||
        holderBalanceBefore - holderBalanceAfter <= to_mathint(spenderAllowanceBefore)
    );
}

The line below states that we are excluding the burn() function in the parametric calls:

Copy
f -> f.selector != sig:burn(address,uint256).selector

burn() is filtered out because, as mentioned earlier, it is intentionally left without permission checks. Including it in the rule would cause it to fail, since any caller could reduce a holder’s balance, which would defeat the rule’s intent.

We already covered requireInvariant in the invariants section, and we are familiar with recording state before and after a method call from earlier sections, so we can jump straight to the assertion.

The assertion below means that if the holder’s balance decreases, it must be due to one of two reasons:

• e.msg.sender == account

  The holder initiated the action, or

• holderBalanceBefore - holderBalanceAfter <= to_mathint(spenderAllowanceBefore)

  The reduction falls within the limits of an approved allowance, which also means that the caller is an approved spender with a nonzero allowance.

Copy
assert (holderBalanceAfter < holderBalanceBefore) => (
    e.msg.sender == account ||
    holderBalanceBefore - holderBalanceAfter <= to_mathint(spenderAllowanceBefore)
);

This specific rule is a modified version of OpenZeppelin’s onlyAuthorizedCanTransfer. The change is that in the original rule, sig:burn(address,uint256).selector was in the assertion, while in this rule onlyHolderAndSpenderCanReduceHolderBalance we filtered it out.

Here’s the Prover run for all the rules in this section.

Full CVL Specification for ERC-20

Here’s the full CVL specification and the Prover run.