In CVL, the type mathint represents unbounded integers, unlike Solidity’s fixed-size types such as uint256. It performs arithmetic without overflow or underflow, which allows reasoning based on pure math. Hence, it exposes overflow or underflow that might otherwise go undetected in unchecked blocks or inline assembly.

In this chapter, you’ll learn:

• What mathint is and why it is the default type
• How to cast from mathint to uint256 and the dangers of doing it
• How we can compare optimized assembly code to the “intended” formula and see if the assumptions hold up

Unchecked Block

In Solidity , an unchecked block disables overflow/underflow checks. Hence in CVL, we should reason using mathint to expose these overflow/underflow situations.

To demonstrate, consider the function average() that accepts two unsigned integers and calculates their average:

Copy
/// Solidity

function average(uint256 x, uint256 y) external pure returns (uint256) {
    unchecked {
        return (x + y) / 2;
    }
}

Let’s formally verify whether the function correctly returns the average of two unsigned integers by writing the rule below:

Copy
/// CVL

rule average_overflow() {
    uint256 x;
    uint256 y;

    
mathint returnVal = average(x, y);

    assert returnVal == (x + y) / 2;
}

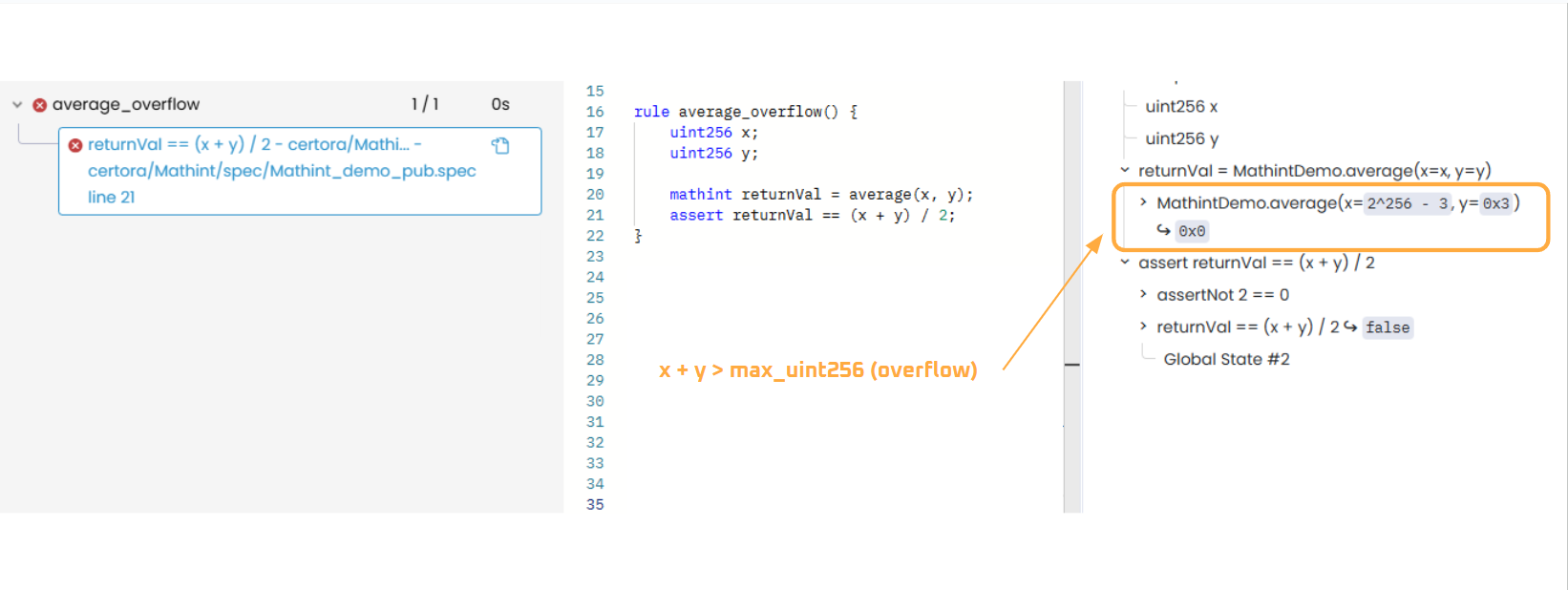
This rule fails, indicating that an overflow occurred during the evaluation of x + y. We’ll explain the reason next.

CVL Arithmetic Evaluates to mathintby Default

The overflow was detected because the right-hand side of the CVL assertion (x + y) / 2 defaulted to type mathint. Certora defines mathint as: “… a type that can represent an integer of any size; operations on mathint can never overflow or underflow.” - source

To see how the overflow was detected, let’s walk through a quick calculation on both sides of the assertion:

Copy
// assert `left-hand side` == `right-hand-side`
assert returnVal == (x + y) / 2;

Let’s use the same values the Prover used (2^256 - 3 and 3, as shown in the image) to calculate the average and understand why the rule failed.

Since the right-hand side(x + y) / 2 evaluates to mathint by default, it correctly computes the average as 2^255:

• x + y = 2^256 (x = 2^256 - 3 and y = 0x3)
• 2^256 / 2 = 2^255

The left-hand side, which is the return value (returnVal) from the Solidity-invoked average() function, evaluated to 0:

• x + y = 0 (with x = 2^256 - 3 and y = 0x3) due to overflow
• 0 / 2 = 0

While the right-hand side correctly computed the average due to unbounded mathint, the left-hand side returnVal (the Solidity function return value) overflowed and wrapped around to zero during the execution of x + y. This led to a mismatch in calculations. Hence, 0 != 2^255, resulting in a failed equality check.

Since CVL arithmetic defaults to mathint, it is safer to write specifications because it removes the possibility of accidentally casting arithmetic operations to a bounded type. However, it does not prevent us from casting to uint256, which can be dangerous, as we’ll see in the next section.

Downcasting mathint to uint256 Can Dangerously Mask Overflow/Underflow Issues

require_uint256 is a built-in CVL function that casts an unbounded mathintto a bounded uint256. According to Certora:

“… the require cast will ignore counterexamples where the cast value is out of range.” - source

To demonstrate, we’ll revisit the previous rule and rewrite it so that CVL operations “deliberately” use uint256 through require_uint256. Hence, important rule violations will be ignored.

Here’s the CVL rule:

Copy
/// CVL

rule average_overflowIgnored() {
    uint256 x;
    uint256 y;

    mathint returnVal = average(x, y);
    
    uint256 numerator = require_uint256(x + y);
    uint256 expectedVal = r
equire_uint256(numerator / 2);


    assert returnVal == expectedVal;
}

In the rule above, the right-hand side of the assertion (expectedVal) was restricted to the uint256 range using require_uint256, which inherently excludes any inputs that would cause an overflow.

As a result, expectedVal always equals returnVal, causing the rule to pass while silently ignoring the overflow:

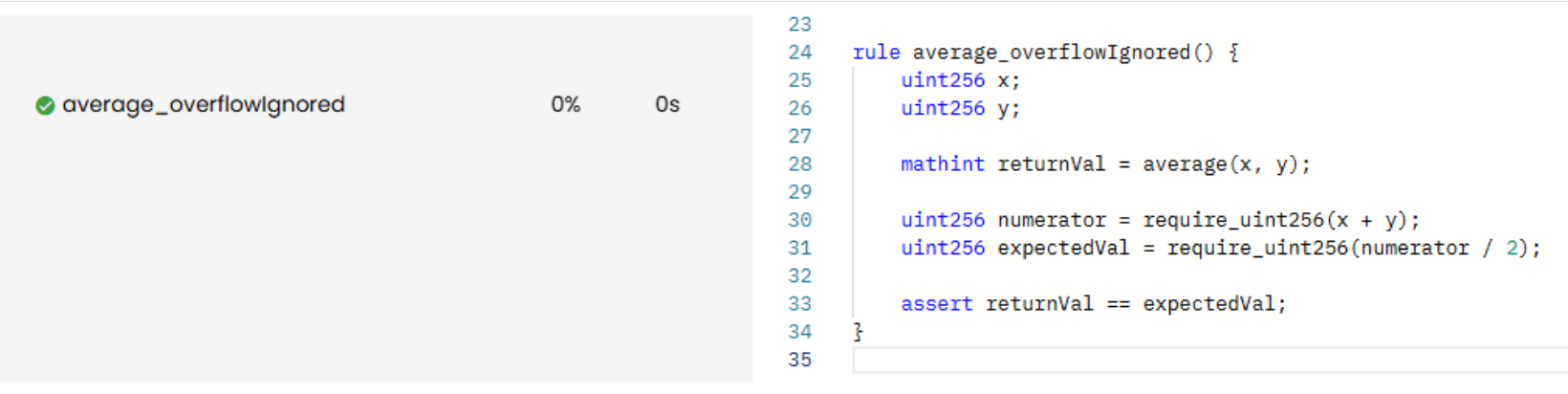
Prover run: link

Inline Assembly

Another source of overflow/underflow is inline assembly. Although it enables gas-efficient code, it bypasses Solidity’s safety checks, including those for overflows and underflows.

To demonstrate, consider the function flawedCeilDiv(), which implements ceiling division using inline assembly. It mirrors the mathematical formula (n + d - 1) / d, which rounds up the result of integer division when there is a non-zero remainder. For example, 6 / 3 evaluates to 2 because the division is exact, while 5 / 2 evaluates to 3 due to the remainder forcing a round-up.

Below is the function implementation:

Copy
/// Solidity

function flawedCeilDiv(uint256 n, uint256 d) external pure returns (uint256 z) {
    assembly { 
        z := div(sub(add(n, d), 1), d) 
    }
}

Here’s how the assembly works:

• add(n, d) → computes n + d
• sub(..., 1) → subtracts 1 → n + d - 1
• div(..., d) → performs the division

Now let’s formally verify whether the formula (n + d - 1) / d is equivalent to the intended behavior of the function flawedCeilDiv():

Copy
/// CVL

rule flawedCeilDiv_overflow() {
    uint256 n;
    uint256 d;

    require d != 0;
    
    mathint returnVal = flawedCeilDiv(n, d);
    mathint expectedVal = (n + d - 1) / d;

    assert returnVal == expectedVal;   
}

Note: The precondition require d != 0 excludes division-by-zero errors for demonstration purposes, as our focus here is on detecting overflow behavior, not the division by zero.

As expected, there is a violation because of an overflow when n + d is being evaluated:

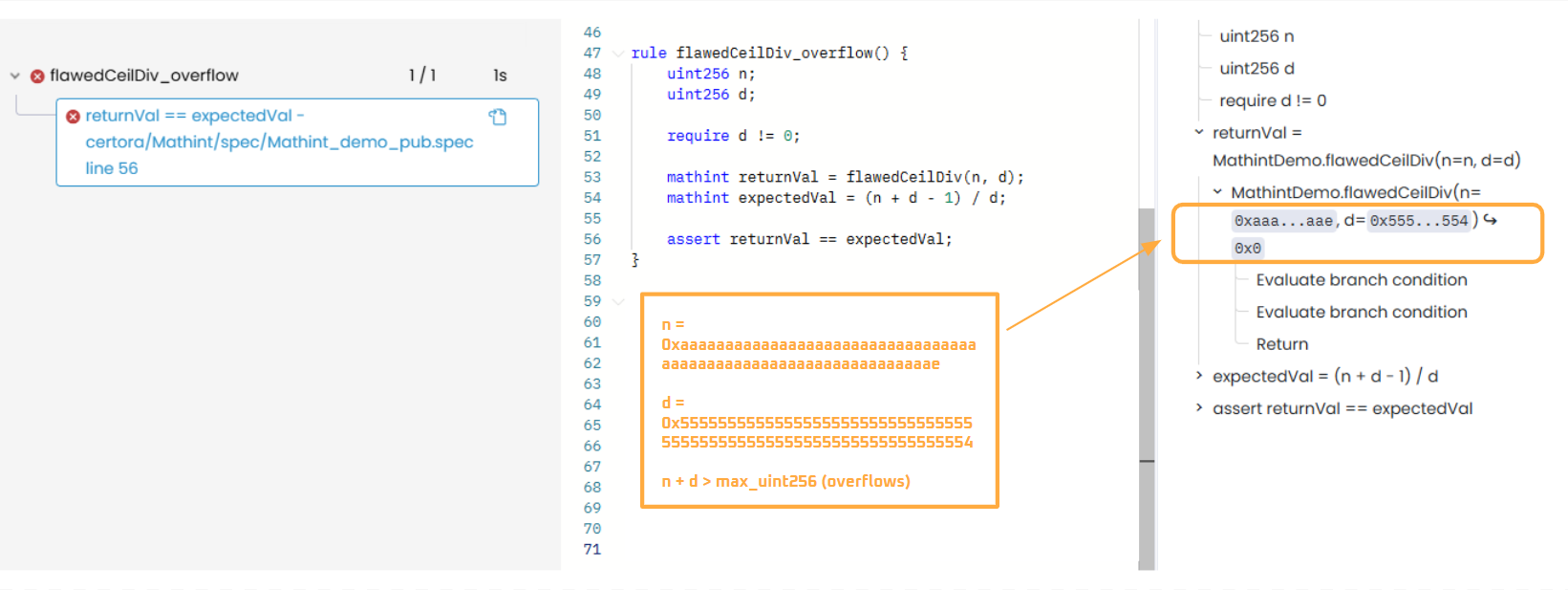
We specifically want to check whether flawedCeilDiv() behaves equivalently to (n + d - 1) / d, but we also unexpectedly discover that an overflow occurs. This highlights why CVL arithmetic operations default to mathint.

Emphasizing That Downcasting mathint Can Mask Overflow/Underflow

To reinforce why downcasting CVL arithmetic operations to uint256 should be avoided, we intentionally restricted expectedVal (a mathint by default) to the uint256 range:

Copy
/// CVL

rule flawedCeilDiv_overflowIgnored() {
    uint256 n;
    uint256 d;

    require d != 0;
    mathint returnVal = flawedCeilDiv(n, d);

    uint256 numerator = require_uint256(n + d - 1);         
    uint256 expectedVal = require_uint256(numerator / d);  
                               
    assert returnVal == expectedVal;
}

As a result, counterexamples beyond the uint256 range are ignored; therefore, the rule passes, hiding the overflow behavior:

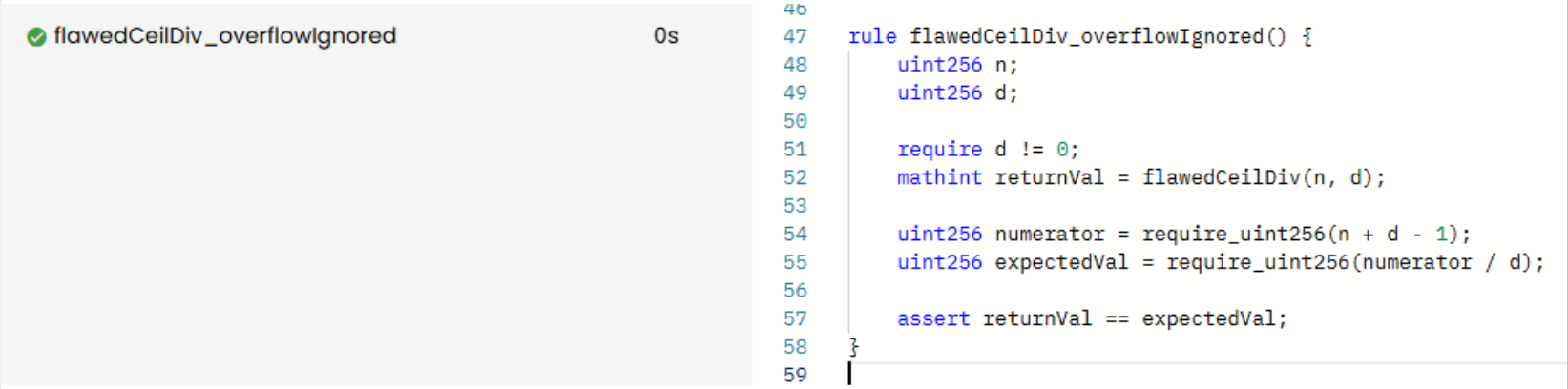
Prover run: link

Verifying Non-Overflow Behavior Of unsafeDivUp

Let’s replace the Solidity function flawedCeilDiv() with an alternative that does not overflow. One such implementation is Solmate’s unsafeDivUp() function, shown below:

Copy
/// Solidity

function unsafeDivUp(uint256 x, uint256 y) external pure returns (uint256 z) {
    /// @solidity memory-safe-assembly
    assembly {
        // Add 1 to x * y if x % y > 0. Note this will
        // return 0 instead of reverting if y is zero.
        z := add(gt(mod(x, y), 0), div(x, y))
    }
}

Note: We changed the function’s visibility to external to avoid using a harness, which is outside the scope of this article.

Now let’s formally verify whether (n + d - 1) / d is equal to the intended behavior of unsafeDivUp():

Copy
/// CVL

rule unsafeDivUp_noOverflow() {
    uint256 n;
    uint256 d;

    require d != 0;
    mathint result = unsafeDivUp(n, d);        
    
    mathint expected = (n + d - 1) / d;
    assert result == expected;
}

As we see, the function holds under the assumption that it behaves equivalently to (n + d - 1) / d. Since CVL operations naturally default to mathint, we can observe that no overflow occurs (even without actively thinking about it).

Prover run: link

Note: The precondition require d != 0 excludes division by zero, as this rule focuses only on verifying non-overflow behavior.

As a final note, Certora provides the following practical guideline:

“The general rule of thumb is that you should use mathint whenever possible; only use uint or int types for data that will be passed as input to contract functions.” - source

Summary

• mathint is an unbounded type in CVL that models arithmetic without overflow or underflow.
• Arithmetic in CVL defaults to mathint, making specifications safer by avoiding accidental casting to bounded types.
• require_uint256 restricts a mathint type to the uint256 range, hence ignoring values beyond max_uint256. Thus, it can hide overflows.
• Use mathint whenever possible, and use uint or int for contract function arguments.