Introduction

In the previous chapter, we demonstrated that Sstore hooks are necessary to verify properties involving changes in mapping values. The hook monitors storage writes, captures old and new values for each key, and executes custom CVL code to update ghost variables.

We demonstrated it by using a simple contract PointSystem that adds points to a user, records them in pointsOf[address], and updates the total in totalPoints:

Copy
contract PointSystem {
    mapping (address => uint256) public pointsOf;
    uint256 public totalPoints;

    function addPoints(address _user, uint256 _amount) external {
        pointsOf[_user] += _amount;
        totalPoints += _amount;
    }
}

However, in practice, contracts optimize for gas efficiency and use unchecked blocks in cases where overflow is practically impossible. For example, the PointSystem contract above can use an unchecked block and be implemented in a way that cannot overflow.

The contract below demonstrates this — an unchecked block is safely used when adding to pointsOf[address]:

Copy
contract PointSystemUnchecked {
    mapping (address => uint256) public pointsOf;
    uint256 public totalPoints;

    function addPoints(address _user, uint256 _amount) external {
        totalPoints += _amount;

        unchecked {
            pointsOf[_user] += _amount;
        }
    }
}

This works because totalPoints += _amount executes first without unchecked, so it reverts on overflow and acts as a circuit breaker. Since every increment to pointsOf[_user] also increments totalPoints, no user can ever accumulate more points than the total points.

However, the Prover does not account for this reasoning. The moment we add an unchecked block, the Prover no longer assumes arithmetic safety. This means it will intentionally assign initial states that trigger wraparound behavior in unchecked operations.

Prover assumes no arithmetic safety in unchecked blocks

To demonstrate, let’s run our specifications for PointSystem against the new PointSystemUnchecked contract. Below are the specifications (both the invariant and the rule), which now fail because of the unchecked block:

Copy
ghost mathint g_sumOfUserPoints { 
    init_state axiom g_sumOfUserPoints == 0;
}

hook Sstore pointsOf[KEY address account] uint256 newVal (uint256 oldVal) {
    g_sumOfUserPoints = g_sumOfUserPoints + newVal - oldVal;
}

invariant sumOfUserPointsEqualsTotalPoints_i() // fails
    totalPoints() == g_sumOfUserPoints;
    
rule sumOfUserPointsEqualsTotalPoints_r(env e, method f, calldataarg args) { // fails
    require totalPoints() == 0 && g_sumOfUserPoints == 0;

    f(e, args);
    assert totalPoints() == g_sumOfUserPoints;
}

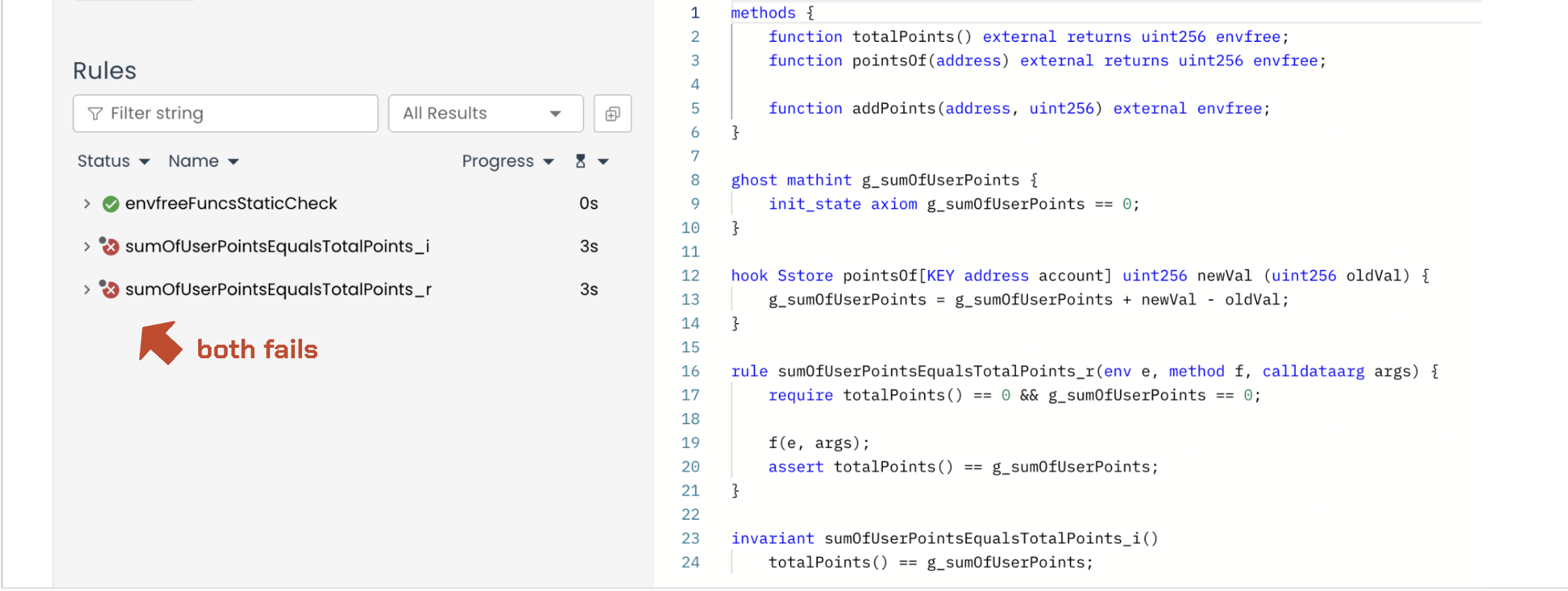
Prover run (fail): link

This raises the question: why do totalPoints and g_sumOfUserPoints diverge when the unchecked block is used? The answer is that the unchecked block triggers the Prover to assign a nonzero initial value to an arbitrary user (pointsOf[address]) to create an overflow scenario along the execution path, while totalPoints starts at zero (the actual initial state). As a result, the Prover tested a state where a user’s points are greater than the total points — an impossible state in the contract.

The Prover sets initial states to intentionally trigger overflow

Now, let’s analyze the call trace for the rule and the invariant we wrote to understand how the violation, a false positive, came about.

Rule call trace

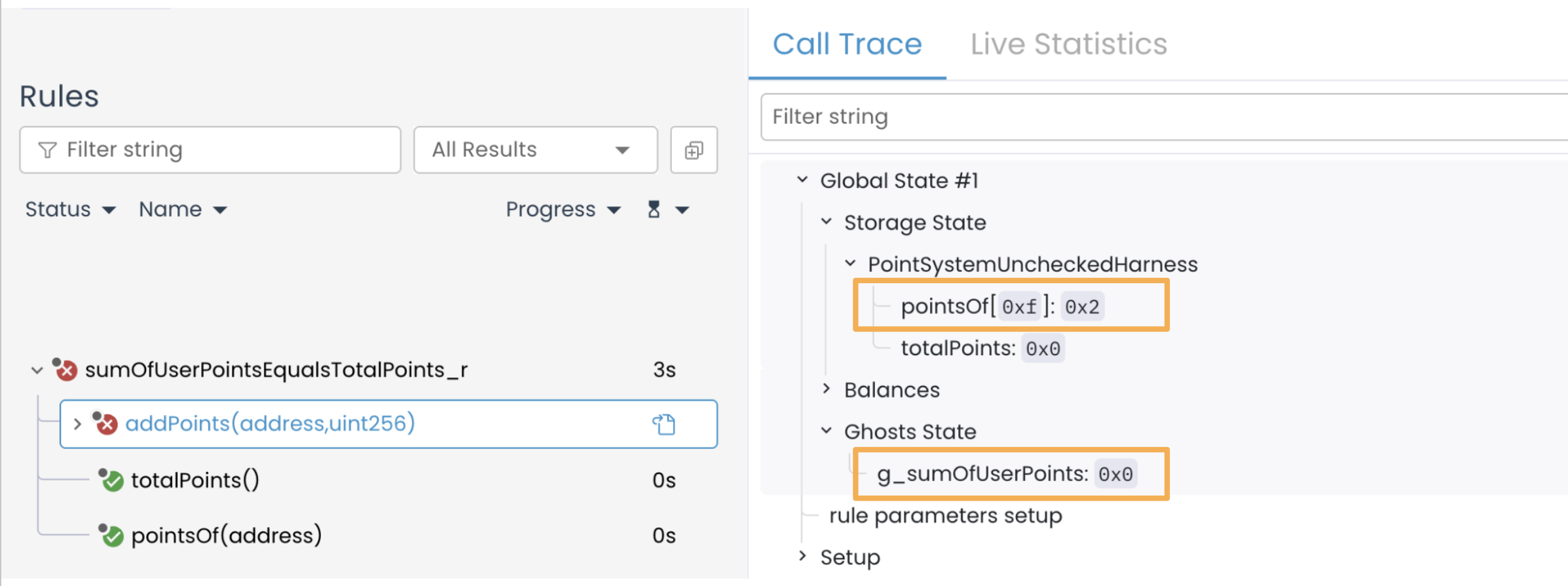
The Prover assigns a nonzero value to address 0xf (pointsOf[0xf] = 0x2) so that later, by adding a sufficiently large value within the uint256 range, it can simulate an overflow:

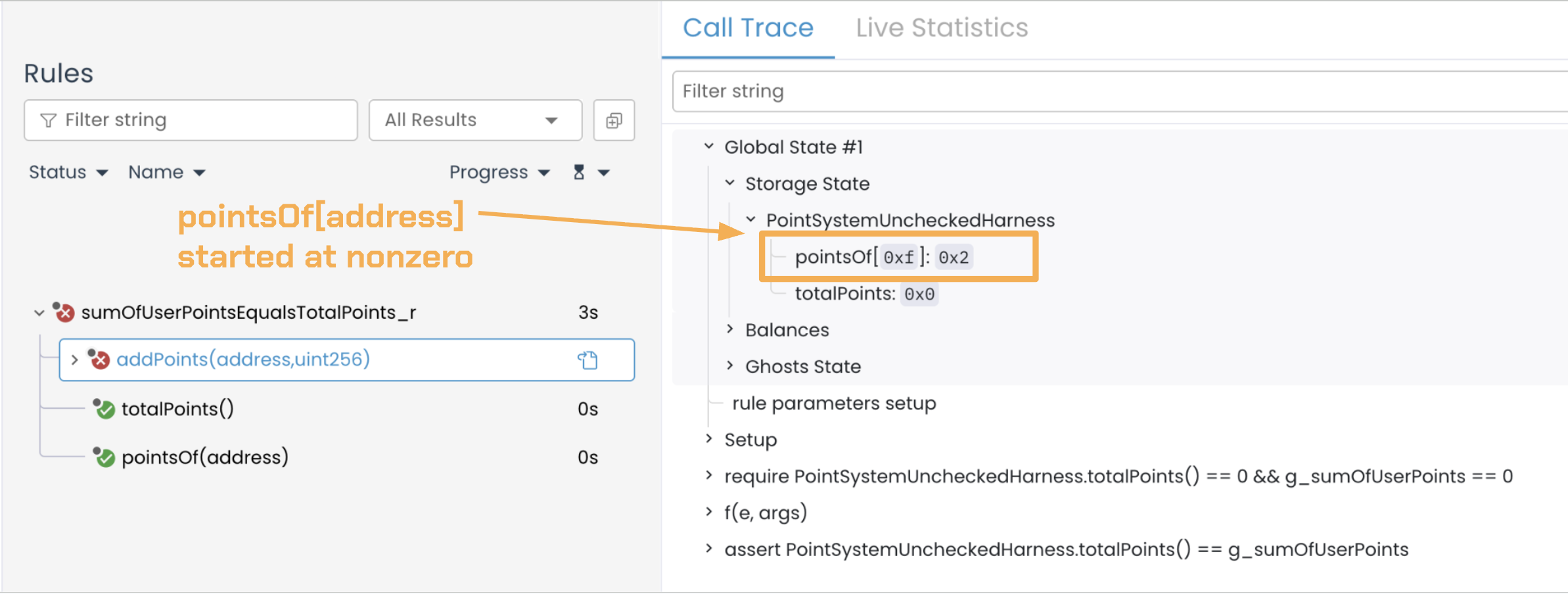
Then the call addPoints(_user=0xf, _amount=2^256 - 2) executes, which results in pointsOf[address] = 0x2 + (2^256 - 2) = 2^256 ≡ 0 (new value wraps to zero due to overflow):

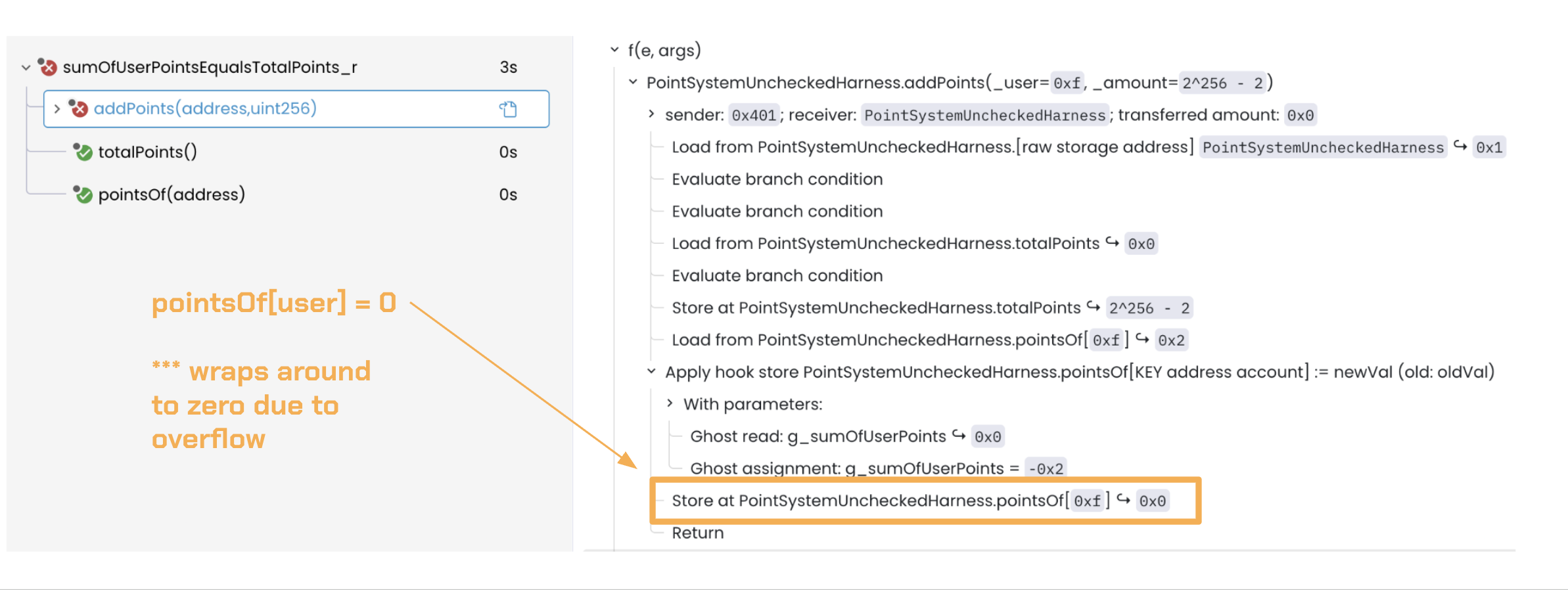
Invoking addPoints() also adds to totalPoints in the contract. Since totalPoints is initially zero, adding 2^256 - 2 (the argument) results in a final value of 2^256 - 2, as shown in the trace below:

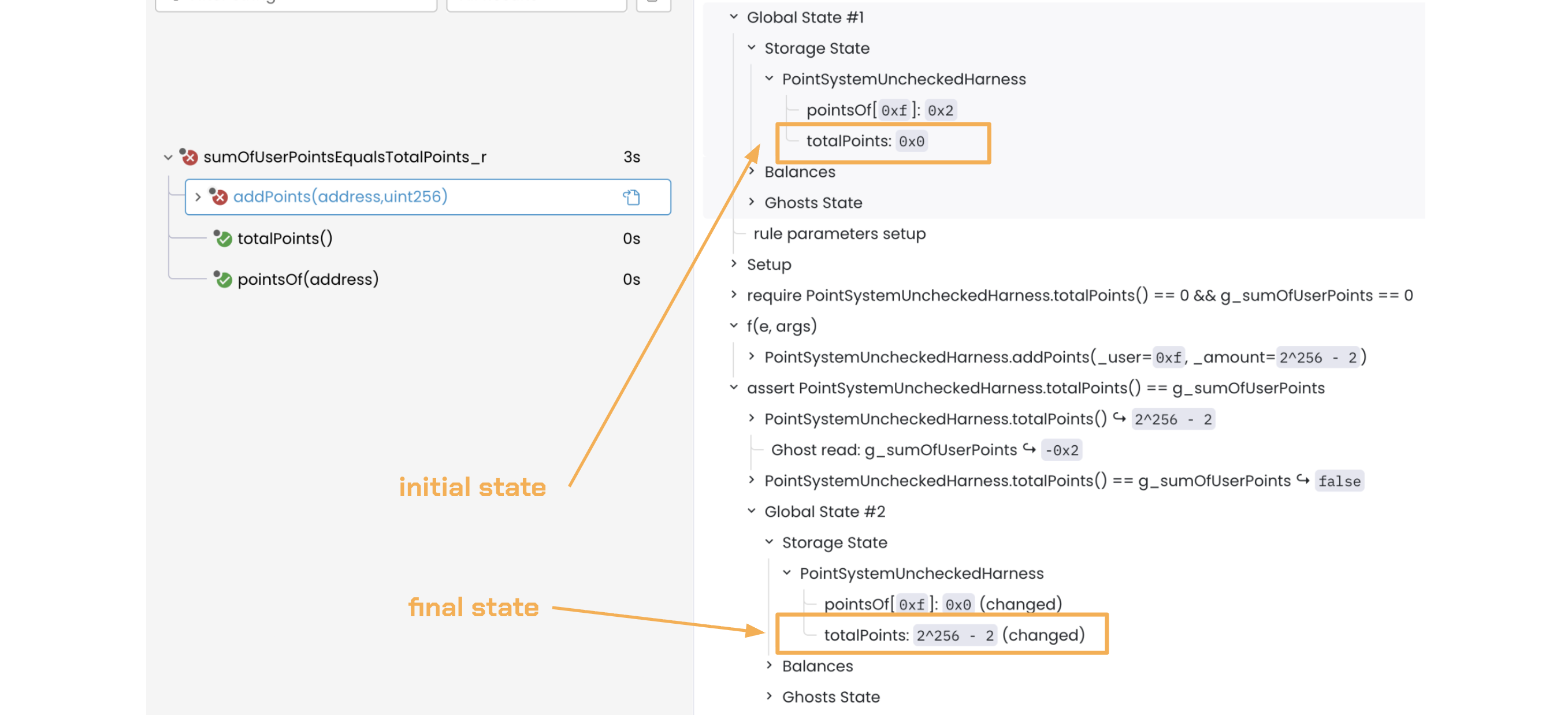
Now, let’s see how the Sstore hook logic calculates g_sumOfUserPoints:

Copy
hook Sstore pointsOf[KEY address account] uint256 newVal (uint256 oldVal) {
    g_sumOfUserPoints = g_sumOfUserPoints + newVal - oldVal;
}

Initial values:

• g_sumOfUserPoints = 0 (initial value)
• pointsOf[0xf] (oldVal) = 0x2 (initial value)

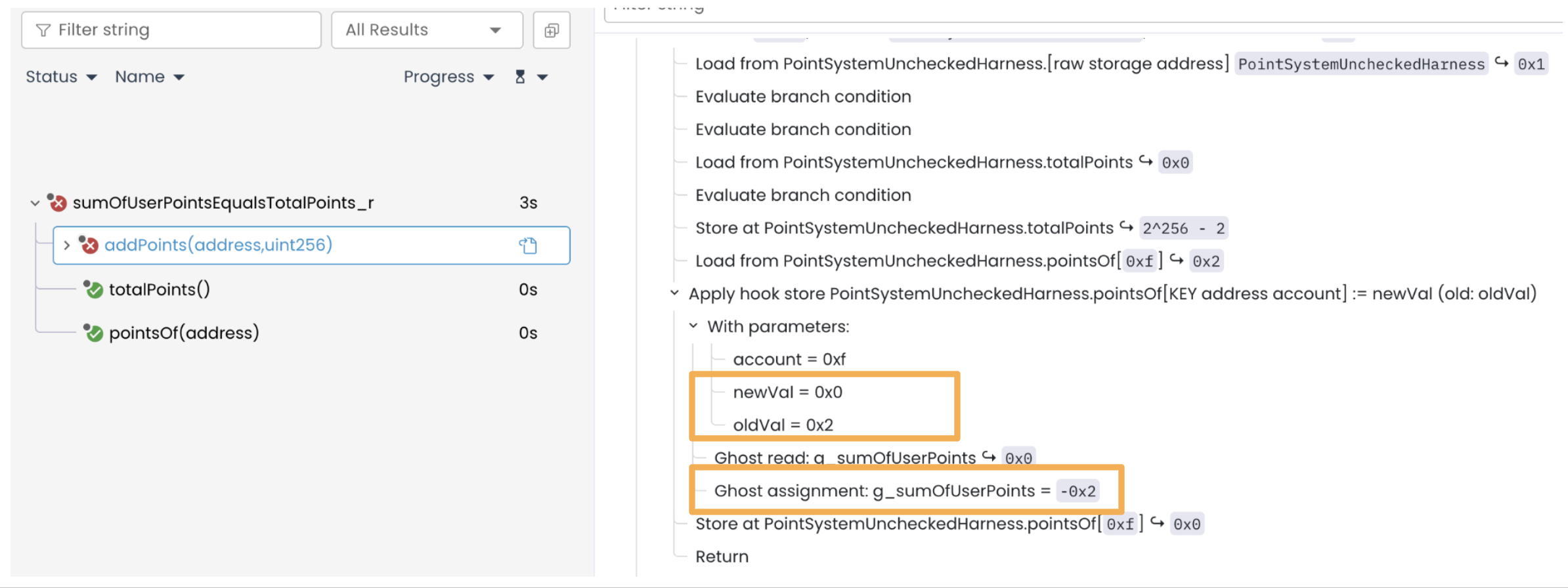
Post-call values after addPoints(0xf, 2^256 - 2):

• pointsOf[0xf] (newVal) = 0x0 (wrapped-around value after adding 0x2 and 2^256 - 2)
• pointsOf[0xf] (oldVal) = 0x2
• g_sumOfUserPoints = 0 + (0x0 - 0x2) = -0x2

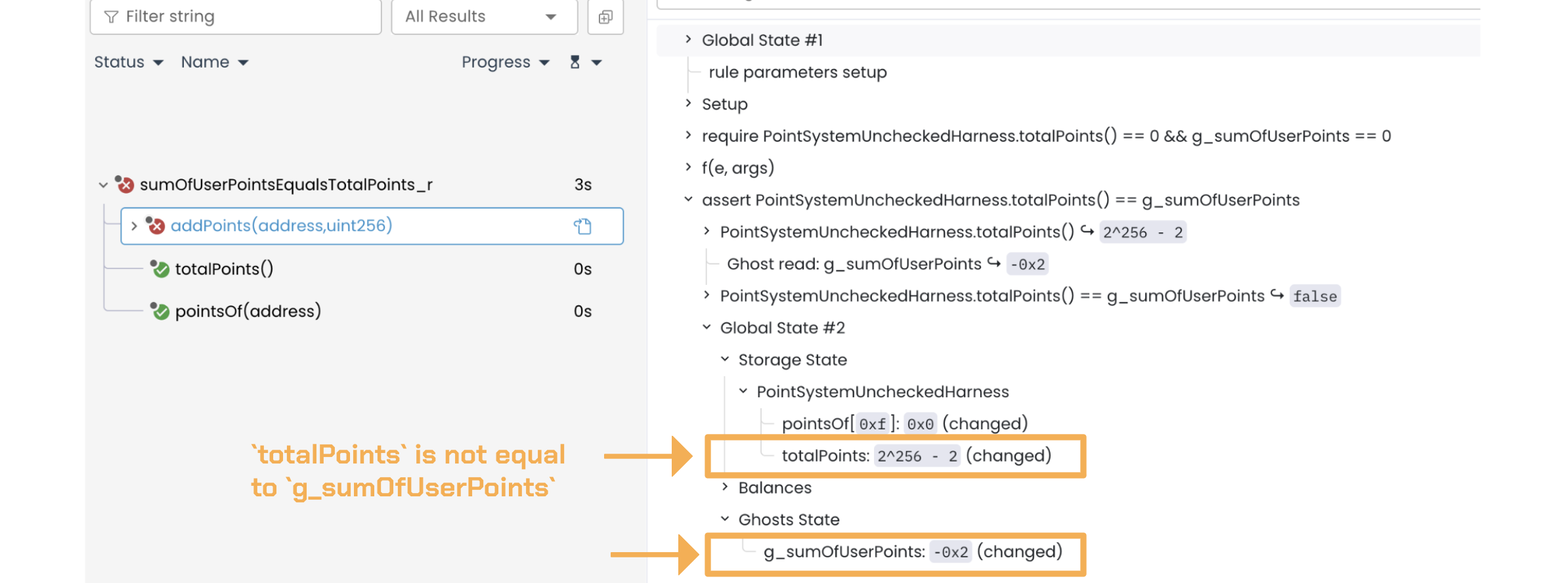
Therefore, totalPoints (2^256 - 2) is no longer equal to g_sumOfUserPoints(-2):

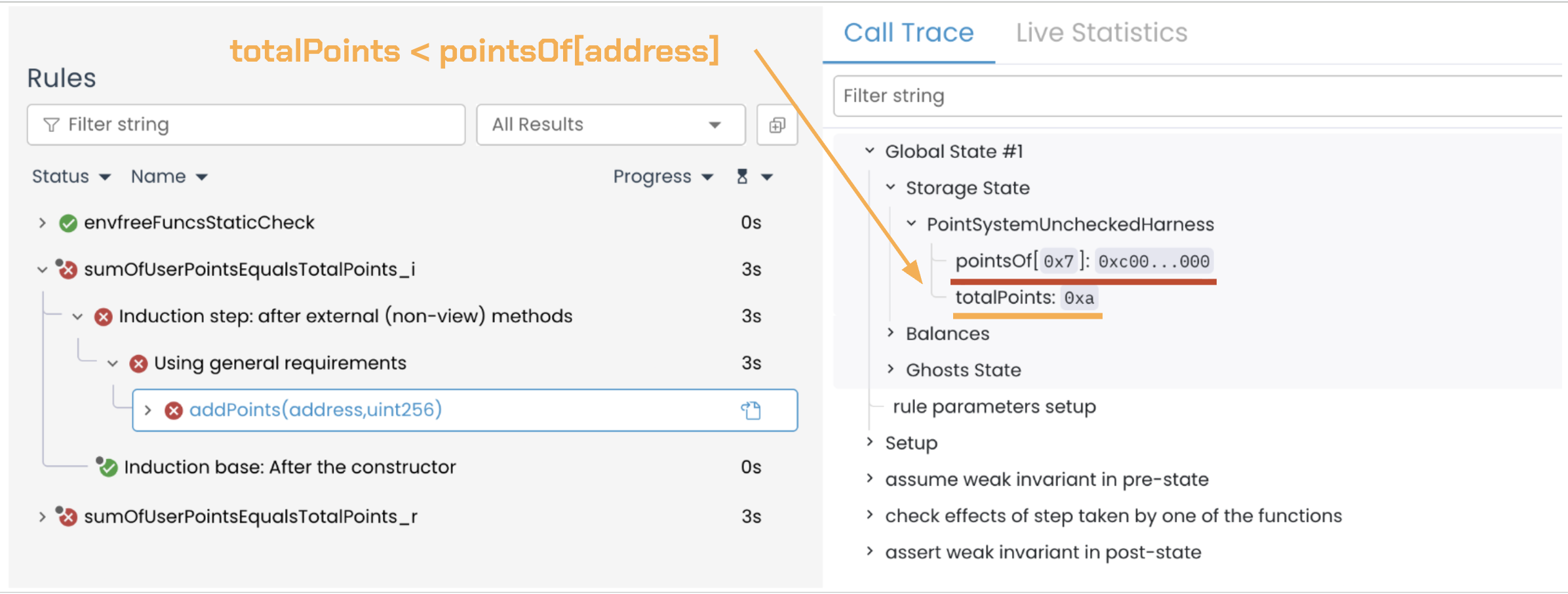
Invariant call trace

The same issue occurred with the invariant. The Prover intentionally seeded pointsOf[address] = 0xc00…000, which is greater than totalPoints in the pre-call state:

We don’t need another call trace to see that, in the final state, accounting inconsistencies happen, and they cause totalPoints to differ from g_sumOfUserPoints.

The core problem

totalPoints and g_sumOfUserPoints both start at zero (as shown in the rule precondition and the invariant’s init_state axiom), but the Prover sets pointsOf[user] to a nonzero value to test an overflow path.

The reason is that overflow cannot occur if pointsOf[user] begins at zero. Adding the max_uint256 value to zero only reaches the uint256 limit, not beyond it. To produce an overflow in the unchecked operation pointsOf[_user] += _amount, the initial value of pointsOf[_user] must already be greater than zero — for example, 2 + (2²⁵⁶ − 2) = 2²⁵⁶ ≡ 0.

This setup creates an unrealistic state where pointsOf[user] > 0 while totalPoints = 0, which cannot occur in real execution since both values always change together within addPoints().

Defining the realistic relationship between the ghost and the storage

Let’s look at the Sstore hook implementation again.

The Sstore hook updates the ghost variable g_sumOfUserPoints by adding the change (newVal - oldVal) from each write to pointsOf[address]:

Copy
hook Sstore pointsOf[KEY address account] uint256 newVal (uint256 oldVal) {
    g_sumOfUserPoints = g_sumOfUserPoints + newVal - oldVal;
}

However, the Prover does not know the realistic relationship between the ghost g_sumOfUserPoints and the storage pointsOf[address].

The g_sumOfUserPoints simply accepts the values it processes, and the Prover cannot determine the realistic value of pointsOf[address] to feed into g_sumOfUserPoints. As a result, the Prover tests all possible values, including unrealistic ones that may cause failures.

What we need to do next is explicitly instruct the Prover on the intended relationship between each individual user’s points (pointsOf[user]) and the sum of user points (g_sumOfUserPoints): g_sumOfUserPoints should always be greater than or equal to pointsOf[user]. We can enforce this relationship using the Sload hook.

Sload hook syntax for mappings

Before we proceed, let’s first look at the syntax and pattern of Sload hooks for mappings. The syntax for hooks is the same as for simple variables, except that for mappings we must include the KEY keyword. For example: storageVar[KEY address user]:

Copy
hook Sload uint256 val balances[KEY address user] {
	// implement hook logic
}

In an Sload hook, the local hook variable val captures the value read from the storage mapping with the key user.

In a contract operation, storage reads occur before the variable is updated or processed. For example, in this Solidity line pointsOf[_user] += _amount, pointsOf[_user] must read its current value before adding _amount.

Therefore, it is important that the “value read” from the storage mapping is accurate before its data is processed and assigned to a ghost variable (via Sstore hooks).

Since the Prover does not know the relationship between the storage variables and the ghost variables, we must explicitly define this relationship as follows:

Copy
hook Sload uint256 points pointsOf[KEY address account] {
	require g_sumOfUserPoints >= points;
}

Here, points is the local hook variable that captures the value read from the mapping pointsOf[address]. This implementation constrains the Prover to explore only states where g_sumOfUserPoints is greater than or equal to points.

Alternatively, we can think of the require as constraining the value of pointsOf[address] (points for any particular user) to always be less than or equal to g_sumOfUserPoints. This means the Prover will never test a scenario where an individual user’s points exceed the total points tracked by the ghost variable.

Using Sload hook fixes ghost-storage inconsistencies

In our specification, we add the Sload hook shown above to enforce that the ghost variable representing the sum of all points (g_sumOfUserPoints) is always greater than or equal to any individual pointsOf[account] value when read from storage.

This prevents the Prover from initializing a state where a single account’s balance exceeds the total sum — a situation that, as we have seen, leads to false positives.

Copy
hook Sload uint256 points pointsOf[KEY address account] {
	require g_sumOfUserPoints >= points;
}

With this in place, both the CVL rule and the invariant succeed, and the property is verified:

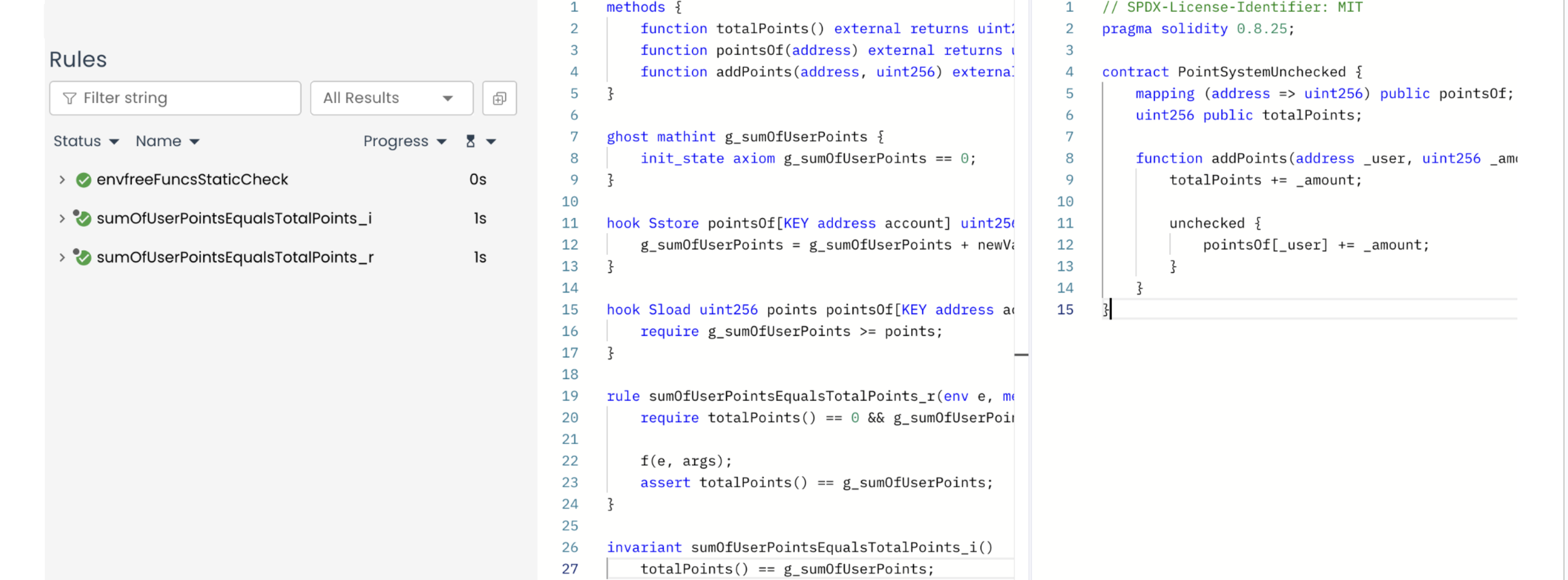
Prover run (verified): link

Summary

• The unchecked block disables Solidity’s built-in overflow checks, which causes the Prover to explore unsafe arithmetic by assigning initial values that trigger overflows to test the implementation.
• These unrealistic initial values can be prevented by using require in the Sload hook, so that the Prover explores states only within the specified bounds, such as requiring that an individual point’s value not exceed the total.