In any correct ERC20 implementation, the sum of all account balances must always equal the total token supply. This property should always remain true throughout any state changes. If a call, whether direct or part of a sequence of calls, violates this invariant, it signals a fundamental flaw in the contract’s logic and design.

In this chapter, we will leverage what we’ve learned about ghost variables and hooks from previous chapters to formally verify this critical invariant.

Adding Smart Contracts For Verification

For this tutorial, we will use the ERC20 contract from the Solmate library, developed by Transmission11. To include this contract in your project, create a new file named ERC20.sol inside the contracts subdirectory of your Certora project directory. Then, copy the code of Solmate’s ERC20 implementation and paste it into that file.

Copy
// SPDX-License-Identifier: AGPL-3.0-only
pragma solidity 0.8.25;

/// @notice Modern and gas efficient ERC20 + EIP-2612 implementation.
/// @author Solmate (https://github.com/transmissions11/solmate/blob/main/src/tokens/ERC20.sol)
/// @author Modified from Uniswap (https://github.com/Uniswap/uniswap-v2-core/blob/master/contracts/UniswapV2ERC20.sol)
/// @dev Do not manually set balances without updating totalSupply, as the sum of all user balances must not exceed it.
contract ERC20 {
    /*//////////////////////////////////////////////////////////////
                                 EVENTS
    //////////////////////////////////////////////////////////////*/

    event Transfer(address indexed from, address indexed to, uint256 amount);

    event Approval(address indexed owner, address indexed spender, uint256 amount);

    /*//////////////////////////////////////////////////////////////
                            METADATA STORAGE
    //////////////////////////////////////////////////////////////*/

    string public name;

    string public symbol;

    uint8 public immutable decimals;

    /*//////////////////////////////////////////////////////////////
                              ERC20 STORAGE
    //////////////////////////////////////////////////////////////*/

    uint256 public totalSupply;

    mapping(address => uint256) public balanceOf;

    mapping(address => mapping(address => uint256)) public allowance;

    /*//////////////////////////////////////////////////////////////
                            EIP-2612 STORAGE
    //////////////////////////////////////////////////////////////*/

    uint256 internal immutable INITIAL_CHAIN_ID;

    bytes32 internal immutable INITIAL_DOMAIN_SEPARATOR;

    mapping(address => uint256) public nonces;

    /*//////////////////////////////////////////////////////////////
                               CONSTRUCTOR
    //////////////////////////////////////////////////////////////*/

    constructor(
        string memory _name,
        string memory _symbol,
        uint8 _decimals
    ) {
        name = _name;
        symbol = _symbol;
        decimals = _decimals;

        INITIAL_CHAIN_ID = block.chainid;
        INITIAL_DOMAIN_SEPARATOR = computeDomainSeparator();
    }

    /*//////////////////////////////////////////////////////////////
                               ERC20 LOGIC
    //////////////////////////////////////////////////////////////*/

    function approve(address spender, uint256 amount) public virtual returns (bool) {
        allowance[msg.sender][spender] = amount;

        emit Approval(msg.sender, spender, amount);

        return true;
    }

    function transfer(address to, uint256 amount) public virtual returns (bool) {
        balanceOf[msg.sender] -= amount;

        // Cannot overflow because the sum of all user
        // balances can't exceed the max uint256 value.
        unchecked {
            balanceOf[to] += amount;
        }

        emit Transfer(msg.sender, to, amount);

        return true;
    }

    function transferFrom(
        address from,
        address to,
        uint256 amount
    ) public virtual returns (bool) {
        uint256 allowed = allowance[from][msg.sender]; // Saves gas for limited approvals.

        if (allowed != type(uint256).max) allowance[from][msg.sender] = allowed - amount;

        balanceOf[from] -= amount;

        // Cannot overflow because the sum of all user
        // balances can't exceed the max uint256 value.
        unchecked {
            balanceOf[to] += amount;
        }

        emit Transfer(from, to, amount);

        return true;
    }

    /*//////////////////////////////////////////////////////////////
                             EIP-2612 LOGIC
    //////////////////////////////////////////////////////////////*/

    function permit(
        address owner,
        address spender,
        uint256 value,
        uint256 deadline,
        uint8 v,
        bytes32 r,
        bytes32 s
    ) public virtual {
        require(deadline >= block.timestamp, "PERMIT_DEADLINE_EXPIRED");

        // Unchecked because the only math done is incrementing
        // the owner's nonce which cannot realistically overflow.
        unchecked {
            address recoveredAddress = ecrecover(
                keccak256(
                    abi.encodePacked(
                        "\x19\x01",
                        DOMAIN_SEPARATOR(),
                        keccak256(
                            abi.encode(
                                keccak256(
                                    "Permit(address owner,address spender,uint256 value,uint256 nonce,uint256 deadline)"
                                ),
                                owner,
                                spender,
                                value,
                                nonces[owner]++,
                                deadline
                            )
                        )
                    )
                ),
                v,
                r,
                s
            );

            require(recoveredAddress != address(0) && recoveredAddress == owner, "INVALID_SIGNER");

            allowance[recoveredAddress][spender] = value;
        }

        emit Approval(owner, spender, value);
    }

    function DOMAIN_SEPARATOR() public view virtual returns (bytes32) {
        return block.chainid == INITIAL_CHAIN_ID ? INITIAL_DOMAIN_SEPARATOR : computeDomainSeparator();
    }

    function computeDomainSeparator() internal view virtual returns (bytes32) {
        return
            keccak256(
                abi.encode(
                    keccak256("EIP712Domain(string name,string version,uint256 chainId,address verifyingContract)"),
                    keccak256(bytes(name)),
                    keccak256("1"),
                    block.chainid,
                    address(this)
                )
            );
    }

    /*//////////////////////////////////////////////////////////////
                        INTERNAL MINT/BURN LOGIC
    //////////////////////////////////////////////////////////////*/

    function _mint(address to, uint256 amount) internal virtual {
        totalSupply += amount;

        // Cannot overflow because the sum of all user
        // balances can't exceed the max uint256 value.
        unchecked {
            balanceOf[to] += amount;
        }

        emit Transfer(address(0), to, amount);
    }

    function _burn(address from, uint256 amount) internal virtual {
        balanceOf[from] -= amount;

        // Cannot underflow because a user's balance
        // will never be larger than the total supply.
        unchecked {
            totalSupply -= amount;
        }

        emit Transfer(from, address(0), amount);
    }
}

Understanding the Challenge

To express our invariant as a CVL expression, we need two values:

1. The total token supply
2. The sum of all account balances

Our contract has a public state variable called totalSupply which keeps track of the total token supply at any state and whose value can be read using the getter function called totalSupply(). However, the core challenge is that the contract does not provide any built-in way to get the total sum of all balances.

The “Solution”

To get the sum of all accounts balances, we will create a ghost variable called sumOfBalances whose initial value will be set to 0 using the init_state axiom. The ghost sumOfBalances will be updated through a store hook each time there is a write operation in the balanceOf mapping.

As we know, the store hook can give us access to both the old and new values of the balance being updated. We use these values to calculate the change and update our ghost accordingly:

Copy
sumOfBalances = sumOfBalances - oldValue + newValue;

For instance, if a user’s balance is increased from 100 to 150, our hook subtracts 100 from and adds 150 to sumOfBalances, correctly increasing the total by 50. By applying this delta calculation for every balance update, our ghost sumOfBalances will track the changes in the contract state, mirroring the sum of all balances.

Once we have both of these values available to the Prover (the actual totalSupply from the contract and our precisely maintained sumOfBalances ghost), we can formally state the invariant using the invariant block in CVL to assert that the total supply is always equal to the sum of all account balances.

Writing the Full Specification Step-by-Step

Let’s now put everything we’ve discussed into practice and write a complete specification that verifies whether the sum of all balances matches the total token supply, by following the steps below:

1. Inside your Certora project directory, navigate to the specs subdirectory and create a new file named erc20.spec.
2. Inside erc20.spec, define a ghost variable called sumOfBalances.

Copy
ghost mathint sumOfBalances;

3. Next, we use the init_state axiom to set the initial value of sumOfBalances to 0 in the invariant base case**.**

Copy
ghost mathint sumOfBalances {
    init_state axiom sumOfBalances == 0;
}

This axiom constrains the ghost variable only in the invariant base case, establishing a consistent post-constructor state. Without this baseline, the prover could assume arbitrary initial values for the ghost, making invariant preservation meaningless.

4. Define a store hook that tracks changes to the balanceOf mapping and updates our ghost variable sumOfBalances accordingly.

Copy
ghost mathint sumOfBalances {
    init_state axiom sumOfBalances == 0;
}

hook Sstore balanceOf[KEY address account ] uint256 newAmount (uint256 oldAmount)  {
    sumOfBalances = sumOfBalances - oldAmount + newAmount;
}

5. Now that we have both values — the contract’s totalSupply() and our ghost sumOfBalances — we can define the core invariant as shown below:

Copy
ghost mathint sumOfBalances {
    init_state axiom sumOfBalances == 0;
}

hook Sstore balanceOf[KEY address account ] uint256 newAmount (uint256 oldAmount)  {
    sumOfBalances = sumOfBalances - oldAmount + newAmount;
}

invariant totalSupplyEqSumOfBalances()
    to_mathint(totalSupply()) == sumOfBalances;

6. Finally, add a methods block that will include the function signature of totalSupply() .

Copy
methods {
    function totalSupply() external returns(uint256) envfree;
}

ghost mathint sumOfBalances {
    init_state axiom sumOfBalances == 0;
}

hook Sstore balanceOf[KEY address account ] uint256 newAmount (uint256 oldAmount)  {
    sumOfBalances = sumOfBalances - oldAmount + newAmount;
}


invariant totalSupplyEqSumOfBalances()
    to_mathint(totalSupply()) == sumOfBalances;

7. Navigate to the confs subdirectory and create a new file named erc20.conf.

Copy
{
    "files": [
        "contracts/ERC20.sol:ERC20"
    ],
    "verify": "ERC20:specs/erc20.spec",
    "msg": "Testing erc20 functionality"
}

Running the Verification

Once you have executed all the above steps, submit the code for verification by running the command certoraRun confs/erc20.conf in your terminal.

Open the verification result provided by the Prover in any web browser of your choice to view a result similar to the image below:

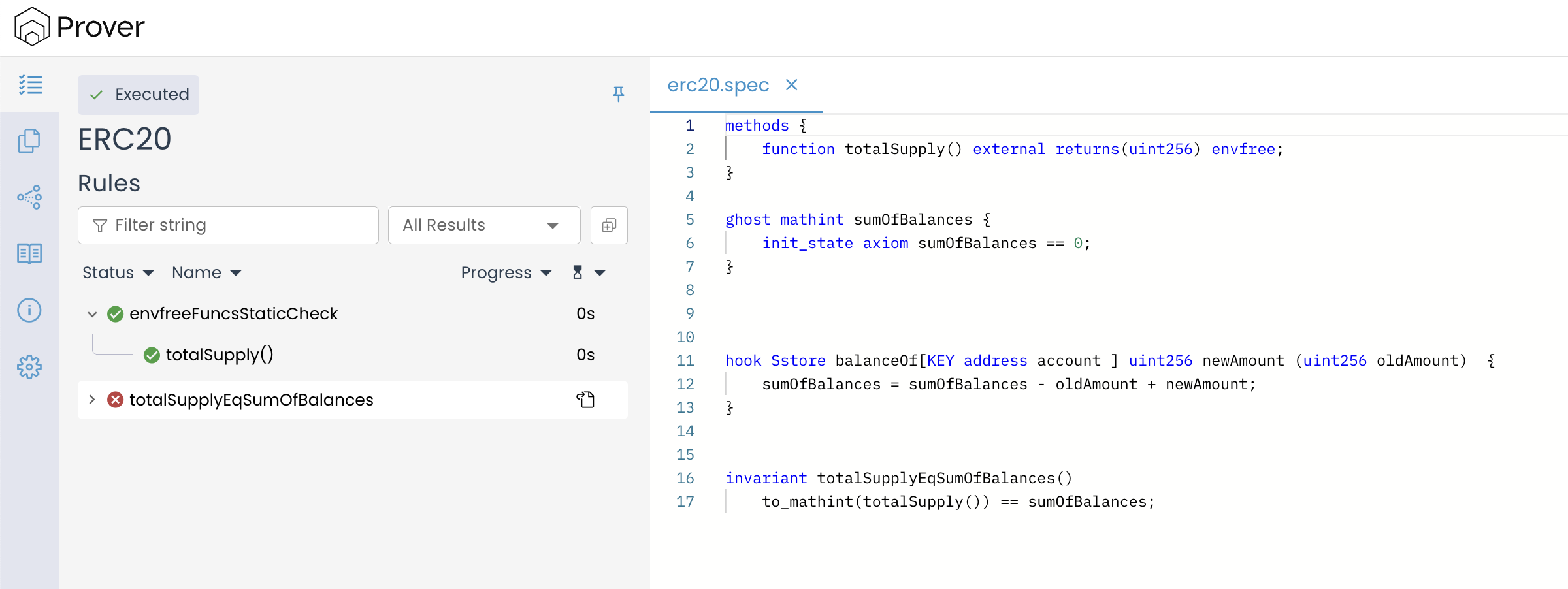
In our verification result, we can see that the invariant check failed in both places: after the constructor call and during method execution.

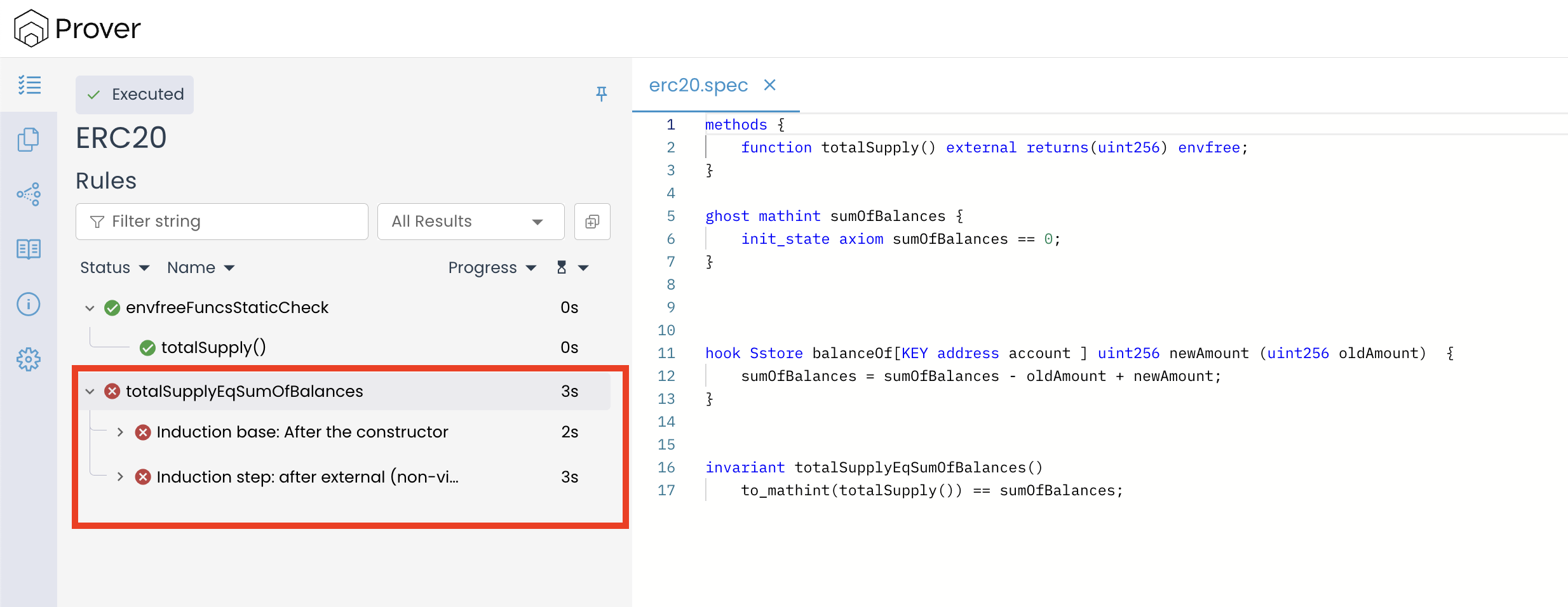
When we click on the “induction base: After the constructor” violation, the Prover recommends adding the optimistic_loop key to your config and setting its value to true, or alternatively increasing loop_iter to a value higher than 1.

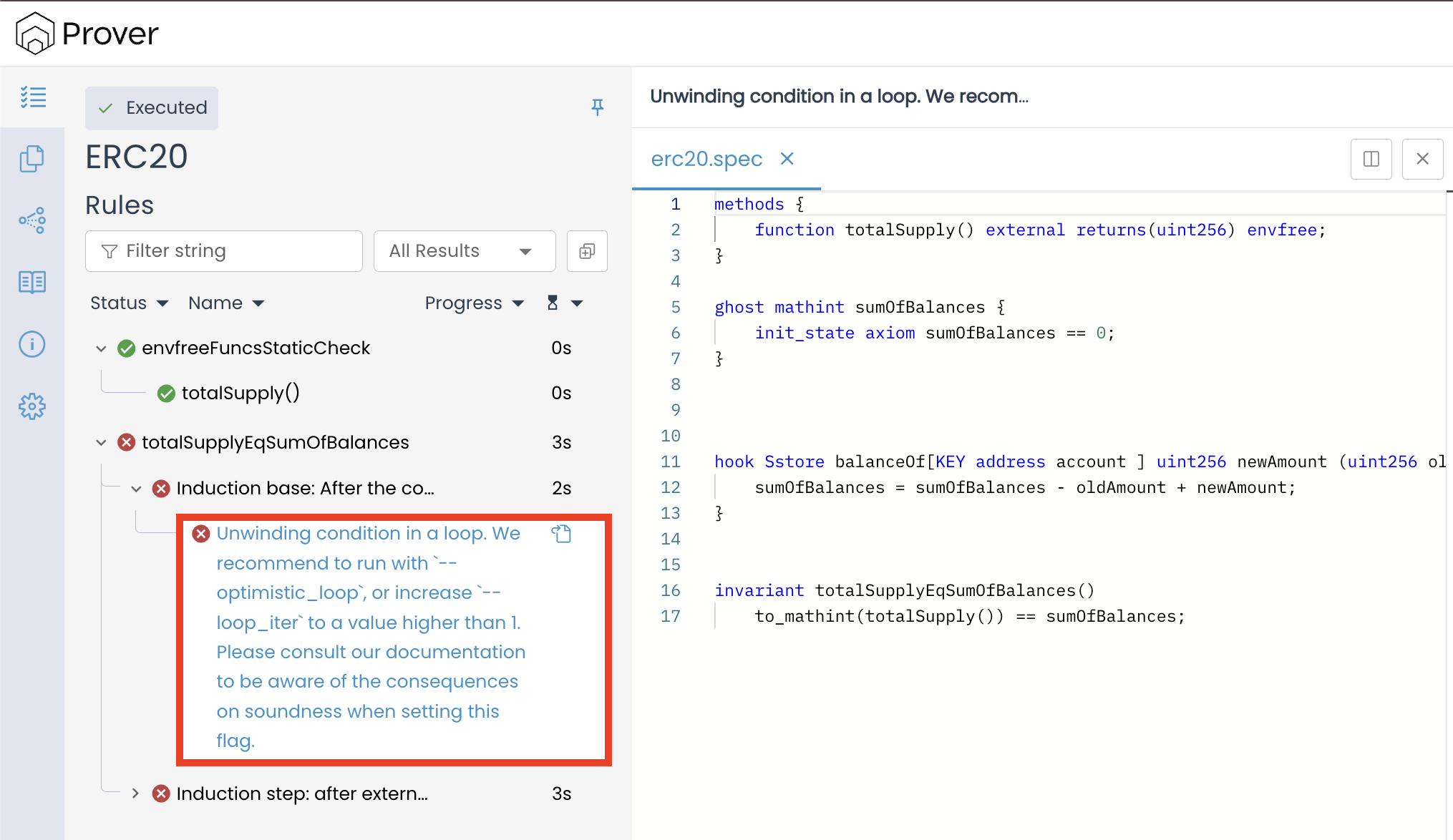
For now, let’s follow the Prover’s recommendation by updating the configuration file with the optimistic_loop key set to true. We’ll explore this issue in greater depth in a later chapter titled “How Strings Lead to Loops?”

Copy
{
    "files": [
        "contracts/ERC20.sol:ERC20"
    ],
    "verify": "ERC20:specs/erc20.spec",
    "optimistic_loop": true,
    "msg": "Testing erc20 functionality"
}

Once done, re-run the Prover by running the command certoraRun confs/erc20.conf in the terminal. In our new verification result, we can see that our invariant successfully passes during constructor execution but fails during method execution, specifically for the transfer() and transferFrom() functions.

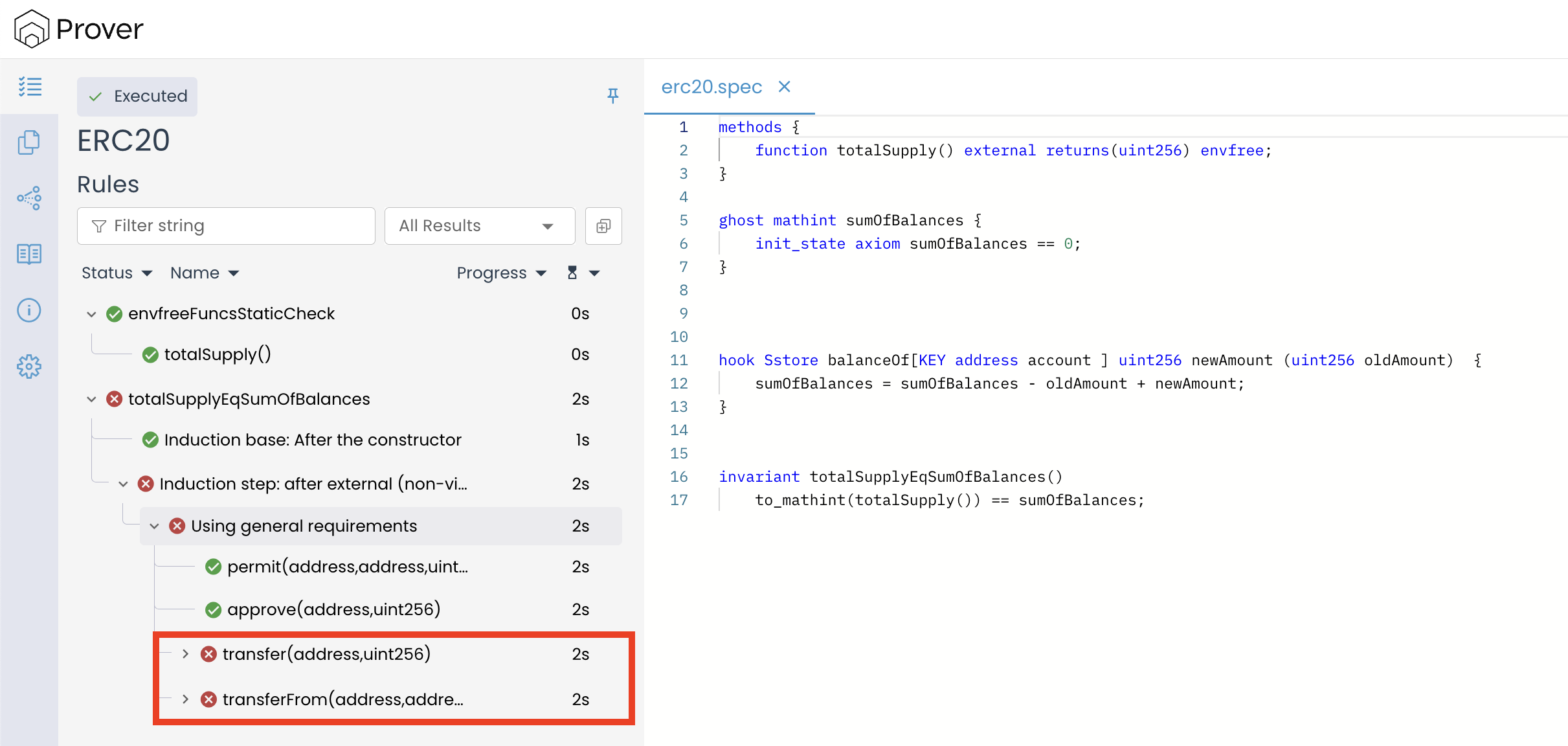
To understand the cause of the violation, click on the call trace of the transfer() or transferFrom() function. In our case, we will analyze the call trace of the transfer() function.

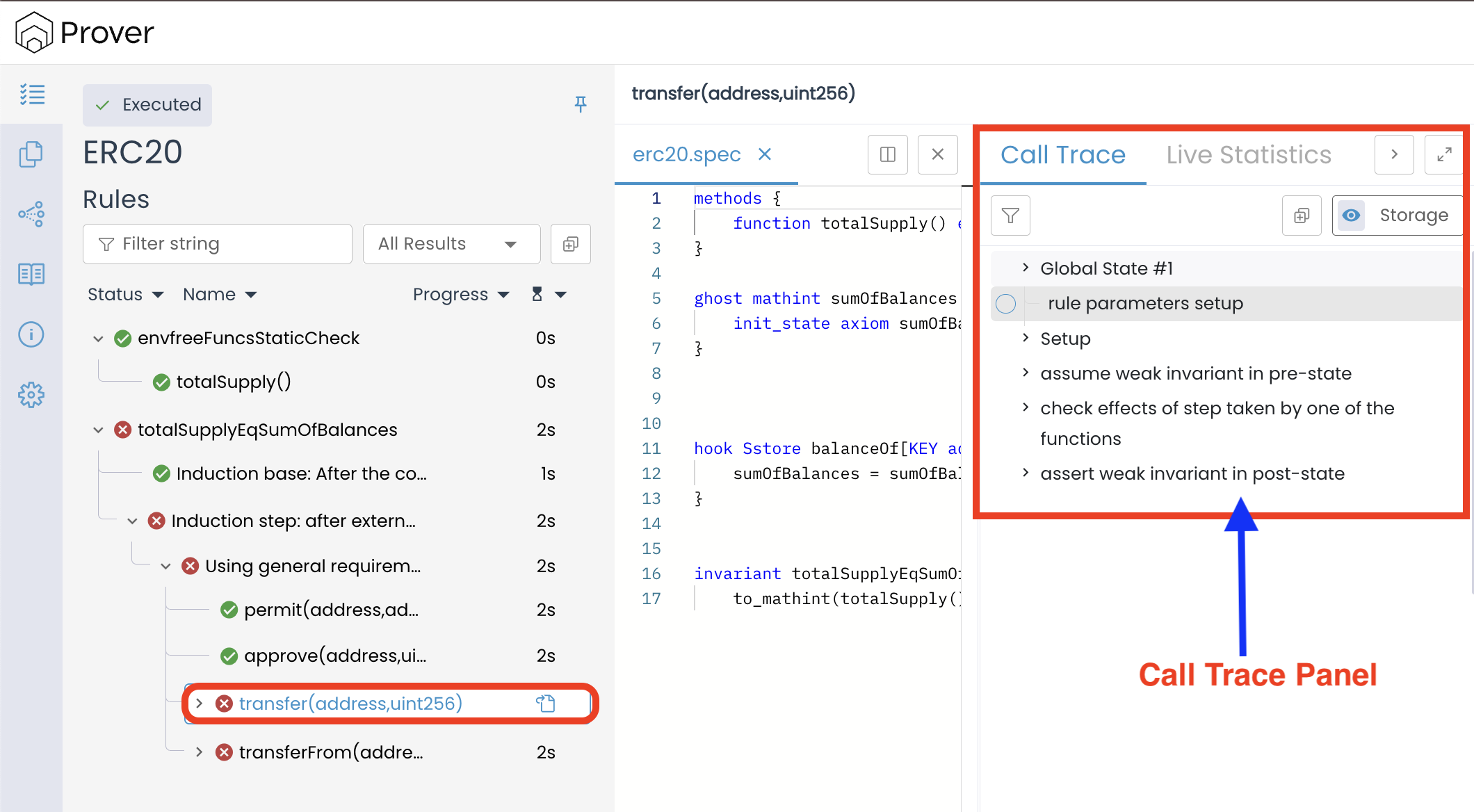
To view the full call trace, click on the “Expand” button available on the top-right corner of the Call Trace panel.

In the call trace, we can see that the initial balances of the individual accounts 0x7 and 0x8200 are set to 2^256 − 4 and 0xf000000000000000000000000000000000000000000000000000000000000000, respectively. In decimal form, these correspond to 115792089237316195423570985008687907853269984665640564039457584007913129639932 and 108890810646419256008710686707116392212123736112785533035372916772359555072000.

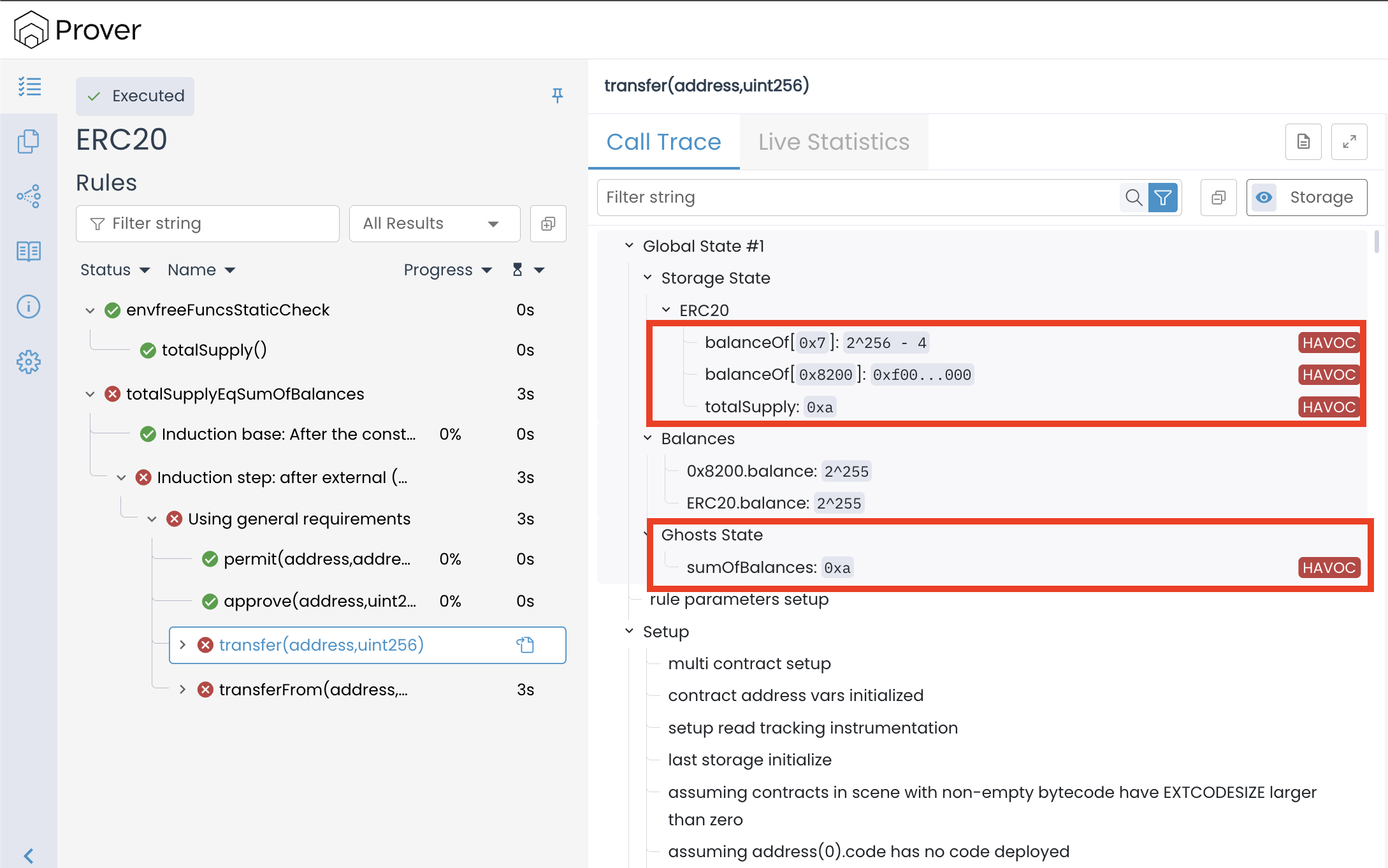
Both of these values are assigned by the Prover through havocing and fall within the numerical range 0 to 2^{256} - 1. However, in any correctly implemented ERC20 contract, no individual account balance should ever exceed the total sum of all balances. In this scenario, both accounts start with balances that are vastly greater than the total supply (0xa) and sumOfBalances, creating an impossible initial state that could never exist in an actual deployment.
The Prover does so because it does not inherently understand the business logic of an ERC20 token; it merely treats the storage as raw data. Unless explicitly constrained, it assumes any uint256 value is a valid starting point.

To avoid this, we specifically need to tell the Prover that the initial individual account balances should not be greater than the sumOfBalances. To do so, we will use the require statement provided by CVL to constrain the values the Prover should consider.

Constraining the Initial Balances using require Statement

In our erc20.spec file, add the code shown below to our store hook to limit the scope of values that can be assigned to the balance of any account. Once done, re-run the Prover to view the verification result

Copy
hook Sstore balanceOf[KEY address account] uint256 newAmount (uint256 oldAmount)  {
    require oldAmount <= sumOfBalances;  //add this line
    sumOfBalances = sumOfBalances - oldAmount + newAmount;
}

In the new result, you’ll notice that the Prover no longer finds any violation.

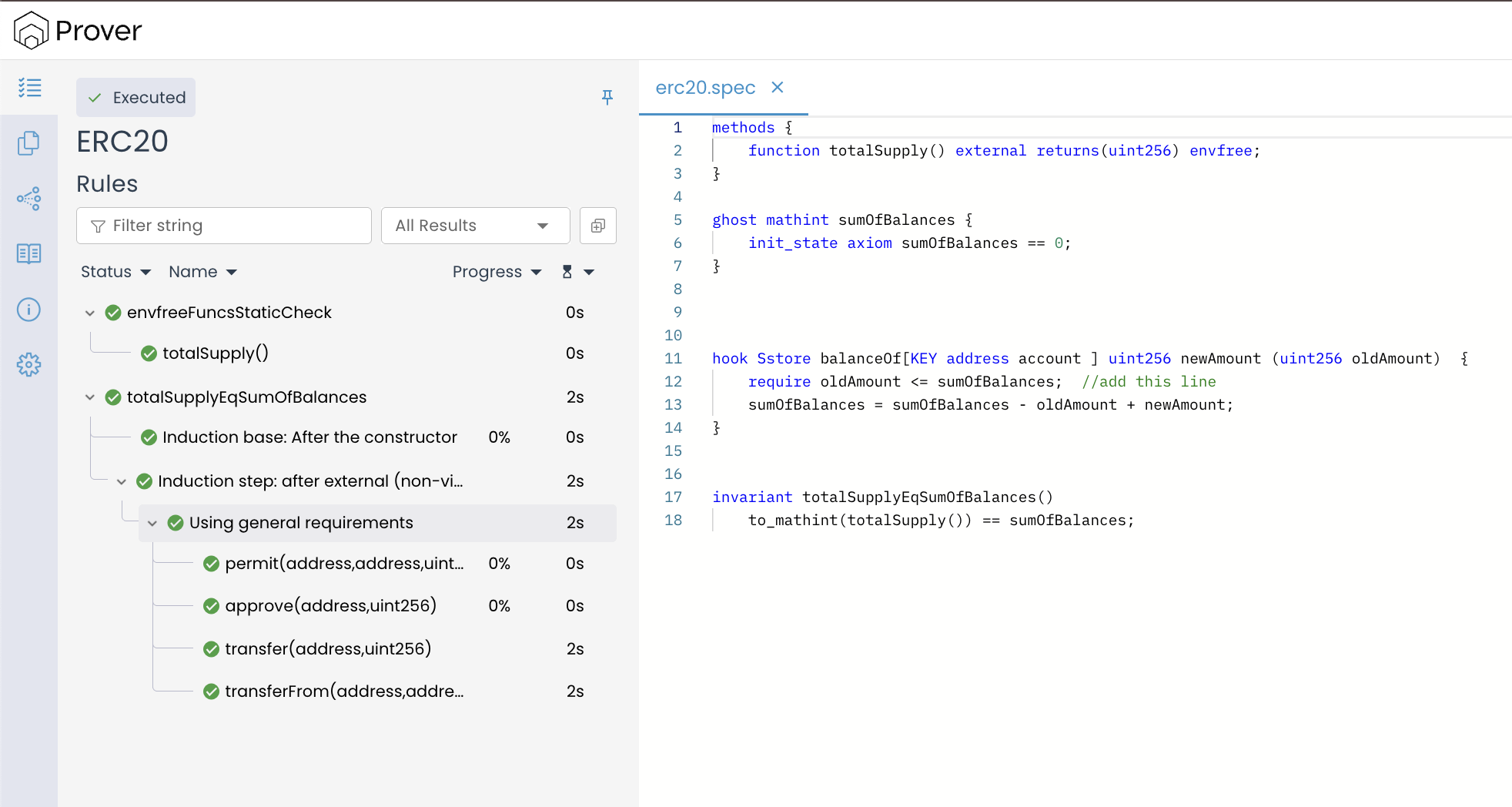
Our invariant totalSupplyEqSumOfBalances passed verification because, after adding the line require oldAmount <= sumOfBalances; in the store hook, the Prover will only explore execution paths where this condition holds true. This effectively rules out counterexamples that rely on a single balance being higher than the total sum (for example, the balance of the sender or receiver in a transfer), ensuring the Prover focuses on scenarios where individual balances remain within the logical bounds of the total supply. As a result, the verification succeeds, confirming that the invariant is preserved under all allowed transitions.

An Alternate Approach: The Load Hook

While adding a constraint to the Sstore hook works, there is another approach where we add the constraint on individual balances inside a Load Hook.

To implement this approach, follow the steps below:

1. Define a load hook on the balanceOf mapping that intercepts every read to balanceOf.

Copy
hook Sload uint256 balance balanceOf[KEY address addr] {}

2. Introduce a constraint inside this hook using require sumOfBalances >= to_mathint(balance);.

Copy
hook Sload uint256 balance balanceOf[KEY address addr] {
    require sumOfBalances >= to_mathint(balance);
}

3. Remove the constraint from the Sstore hook so that we are relying solely on the load hook logic.

Copy
hook Sstore balanceOf[KEY address account] uint256 newAmount (uint256 oldAmount)  {
    require oldAmount <= sumOfBalances;  //remove this line
    sumOfBalances = sumOfBalances - oldAmount + newAmount;   
}

Here’s what the updated specification should look like after the changes suggested above:

Copy
methods {
    function totalSupply() external returns(uint256) envfree;
}

ghost mathint sumOfBalances {
    // Constraining pre-constructor ghost value through axiom
    init_state axiom sumOfBalances == 0;

}

// Added a load hook on balanceOf mapping
hook Sload uint256 balance balanceOf[KEY address addr] {
    // Introduce a constraint
    require sumOfBalances >= to_mathint(balance);

}

hook Sstore balanceOf[KEY address account] uint256 newAmount (uint256 oldAmount)  {
    // Delta Update
    sumOfBalances = sumOfBalances - oldAmount + newAmount;

}


invariant totalSupplyEqSumOfBalances()
    to_mathint(totalSupply()) == sumOfBalances;

If you re-run the verification with this change (removing the require from the Sstore hook and keeping it only in the Sloadhook), the invariant totalSupplyEqSumOfBalances will still pass.

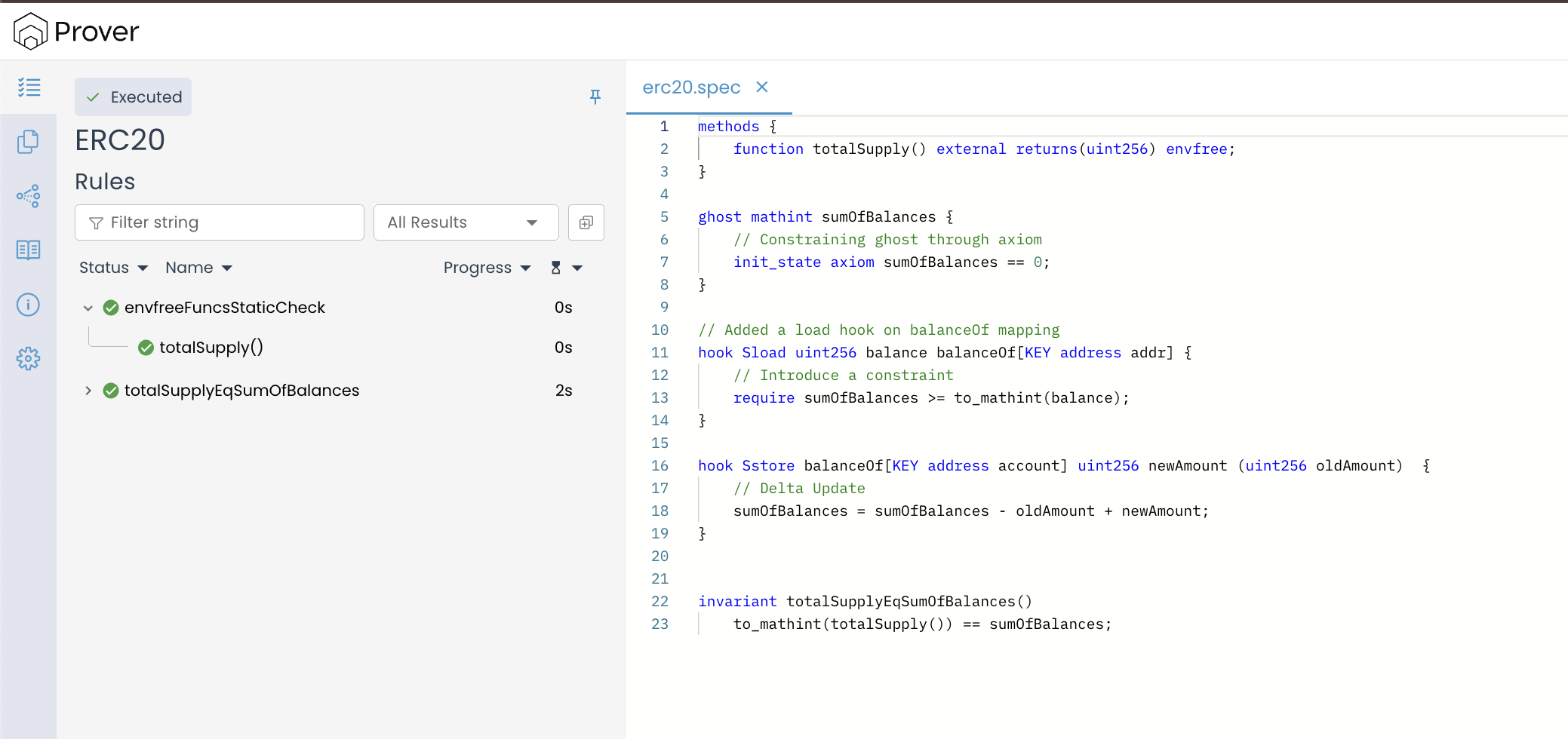
This works because the load hook explicitly filters out any state where an individual account balance is larger than the total sum of all balances. If the Prover tries to build a counterexample using such an impossible initial state, it will eventually read that balance while evaluating the contract logic. The moment this read occurs, the require  statement inside the load hook checks whether that balance is consistent with our ghost variable. Since the balance is unrealistically large, the condition fails, and the Prover is forced to discard that entire execution path.

Sstore vs. Sload: Where to Place Constraints?

Both versions “work” because they exclude the impossible states that would violate our invariant, but the load hook approach provides a more reliable and comprehensive safeguard. Let’s unpack why:

What the Store Hook Actually Guarantees

When we put the constraint in the store hook:

Copy
hook Sstore balanceOf[KEY address account] uint256 newAmount (uint256 oldAmount) {
    require oldAmount <= sumOfBalances;
    sumOfBalances = sumOfBalances - oldAmount + newAmount;
}

In the above code, we are effectively telling the Prover: “Whenever you write to balanceOf[account] , make sure the previous value (oldAmount) was not larger than sumOfBalances”

This creates a blind spot:

1. If the Prover never writes to a certain balanceOf[addr] slot, then this hook is never triggered for that address.
2. This means the Prover is still free to start from a weird initial value (via havoc), like balanceOf[addr] = 2^{256} - 1, even if sumOfBalances = 10.
3. As long as the contract doesn’t try to write to that slot, the require in Sstore is never checked, and the impossible state is allowed to persist during reads and logical reasoning.

In short, the store hook only says: “If you ever touch this slot by writing to it, then the previous value must be reasonable.” It does not say: “All balances are always reasonable whenever you look at them.”

What the Load Hook Guarantees Instead

Now, look at the load hook version:

Copy
hook Sload uint256 balance balanceOf[KEY address addr] {
    require sumOfBalances >= to_mathint(balance);
}

This runs every time the Prover reads a balance from balanceOf. Here, we are telling the Prover: “Whenever you read a balance, that balance must be less than or equal to sumOfBalances”

This has two important effects:

1. The Prover cannot use an impossible balance in any calculation. If it tries to assume balanceOf[addr] is bigger than sumOfBalances and then reads it, the require in the load hook fails, and that execution path is immediately discarded.
2. This applies even if the slot was never written to. The Prover might havoc balanceOf[addr] to some arbitrary value at the start, but the moment it reads that value, the load hook checks it. If the value is impossible, that whole path is thrown away.

The load hook acts like a global sanity check: “Any balance you ever look at must make sense with respect to the ghost sumOfBalances”

This is why, when we care about keeping sumOfBalances aligned with real balances and avoiding impossible ERC20 states, the load hook approach is usually the better choice.

Conclusion

In this chapter, we verified the fundamental ERC20 invariant: Total Supply = Sum of All Balances.

We achieved this by using a ghost variable to track the aggregate sum and hooks to synchronize that ghost with the contract’s storage. Crucially, we demonstrated why placing constraints in an Sload hook is often safer than in an Sstore hook. By policing values whenever they are read, we effectively closed the “blind spot” where the Prover could otherwise assume impossible initial states.

These techniques allow you to prove high-level business rules on top of low-level storage, ensuring your verification focuses solely on valid, realistic contract behaviors.