The interest rate model of Aave V3 and Compound V2
Interest rates in TradFi (traditional finance) are largely determined by central banks and influenced by market factors. In contrast, DeFi interest rates are algorithmically determined by the demand for loans and the supply of funds from lenders.
Concepts in this article will be explained through the lens of Aave, a leading DeFi lending/borrowing protocol on Ethereum. Compound V2’s interest rate model is identical, with minor implementation differences. You may encounter differences when comparing the implementations of other lending/borrowing protocols.
A lending protocol uses smart contracts to aggregate liquidity from lenders, and allow for loans to be taken against this combined liquidity by borrowers. We sometimes refer to the liquidity as “funds” or “capital.”
Lenders (a.k.a Suppliers) will earn interest based on the liquidity they provide. Borrowers will be obligated to pay interest on their loan.
Lending protocols often set aside a “reserve factor” — a percentage of capital supplied by lenders that they do not receive interest on. The interest from this capital instead goes to the protocol, and is sometimes called the “spread.”
The degree of borrowing influences interest rates — we call this “borrow demand.” The greater the percentage of deposits loaned out, the more the interest rates rise. We refer to the degree of borrowing relative to the supply of borrowable funds as “utilization.” If there are no borrowers, utilization is 0% and if the deposits are fully loaned out, utilization is 100%. The value of utilization is used as the sole driver of interest rates.
The following diagram illustrates this — we will explain each step throughout this article.

Authorship
This article was written by Calnix with animations created by Aymeric Taylor.
Utilization Formula
As mentioned earlier, Utilization is determined by borrow demand.
Utilization is typically calculated as such:
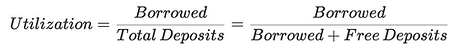
Note that borrow demand is relative to total deposits. If the total deposits increases but borrow demand stays the same, utilization goes down.
How utilization drives borrow interest rates
Utilization in turn determines borrow interest rates

In a properly designed protocol, changes in utilization lead to rising/falling interest rates as explained below.
When utilization rises: (indicative of high demand for borrowing)
- Borrow and supply interest rates increase
- Lending is incentivized and borrowing is disincentivized
- As a consequence, idle liquidity increases, and borrow demand falls, leading to a lower level of utilization.
When utilization falls: (indicative of excess idle liquidity)
- Borrow and supply rates decrease
- Borrowing is incentivized and lending is disincentivized
- As a consequence, idle liquidity decreases, and borrow demand rises; leading to a higher level of utilization.
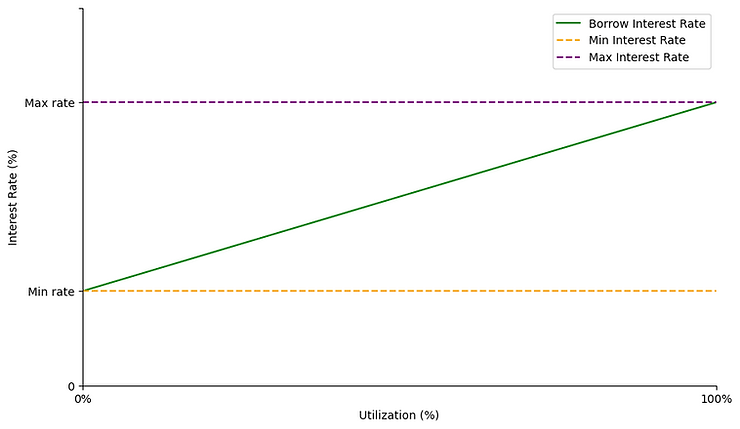
The function that translates the utilization level to the borrow interest rate is defined by the interest rate model. The parameters are usually set by protocol governance.
Calculating the relationship between the borrow interest rate and the supply interest rate
We now look at the final relationship in the chain

The relationship is determined as follows:

Not all lending protocols set the supply interest rate using this formula. Notably, Compound V3 calculates the supply interest rate directly as a function of utilization and does not factor in the borrow rate.
Example: Consider a lending protocol where the borrow rate is 10% and the utilization level is 50%. In this case, the interest rate enjoyed by depositors would be:
- Supply Rate = Borrow Rate × Utilization level
- Supply Rate = 10% × 50% = 5%
Depositors would earn an interest rate of 5% on their deposits.
Below we see a plot of supply interest rate as a function of the borrow interest rate. When utilization is zero, lenders don’t earn any interest.
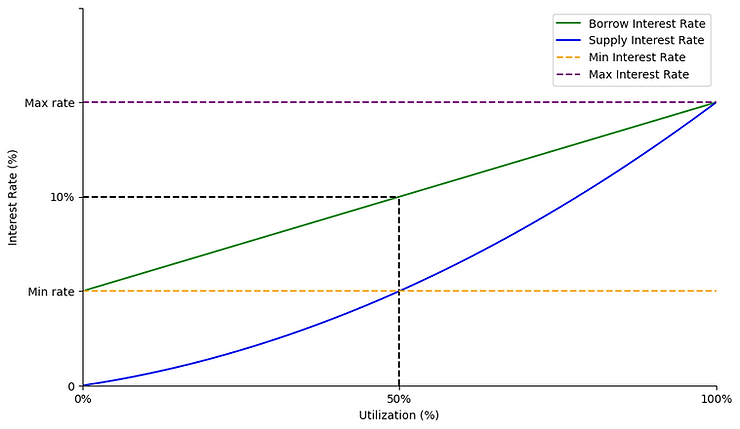
What is the motivation for multiplying borrow interest with utilization?

If 50% of the funds are borrowed, only half of the capital provided by lenders is lent. If the borrower pays 10% on half the assets available, the lender gets 5% on their capital. If we paid the lenders 10% on their entire capital, but only half of it was borrowed, then the protocol would not be able to meet its obligations.
Consider the case where $100 is supplied to the protocol and $50 is borrowed. If the borrower pays 10% interest, they would pay $5 to the protocol. But if the protocol pays the suppliers 10% interest on the $100, it would owe them $10 — which it hasn’t earned from borrowers.
Adding in a reserve factor: accounting for spread
While the previous example is useful for our understanding, it ignores the spread we mentioned at the start – the cut that goes to the protocol, which could reflect fees, treasury contribution, etc.
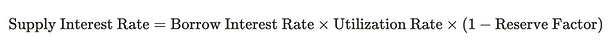
The reserve factor allocates a portion of the borrow interest to the protocol, with the rest divvied out to depositors.
Worked Example: Assume a lending protocol where the borrow rate is 10%, utilization level is 50% and reserve factor 20%. In this case, the interest rate enjoyed by depositors would be:
- Supply Rate = Borrow Rate × Utilization level × (1 – Reserve Factor)
- Supply Rate = 10% × 50% × (1 – 20%) = 5% × (80%) = 4%
As you can see, a fifth of the borrow interest is siphoned off, and depositors now earn 4% on their deposits.
Real interest rate models
DeFi applications try to encourage the utilization to be around a certain percentage, usually between 80-95%, this is called the “optimal utilization.”
It is undesirable for all the available funds to be lent out (100% utilization). Under this circumstance, lenders cannot withdraw. Therefore, when all the capital is used up, we want strong incentives in place for lenders to supply more funds to the protocol — or for borrowers to return borrowed assets. Therefore, the supply curve is typically piecewise linear and “kinked” — it rises slowly up to the optimal utilization point, then rises faster.
Formula for piecewise linear kinked function
Any interest rate model must be a function of Utilization 𝑈 since
Aave’s piecewise linear kinked interest rate model is as follows.
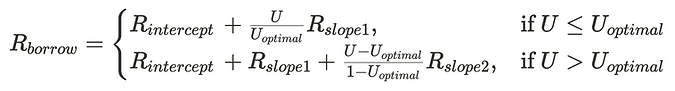
To get an intuition for the formula, we can rearrange the equations in the form of y = mx + c

The following animation illustrates what each part of the formula does

Note that 𝑈 is the independent variable here, Rborrow is a function of that and other parameters that are determined by protocol governance.
The "kink" area of the curve is what the protocol considers "optimal." If the utilization exceeds that level, the interest rates start rising quickly to incentivize lenders to supply more capital or borrowers to pay down loans.
DAI example
Let’s look at Aave’s DAI interest rate model, as defined by the contract DefaultReserveInterestRateStrategy on Ethereum. The four essential parameters (U_optimal, R_intercept, R_slope1, R_slope2) are publicly accessible from the smart contract.
Here is the smart contract address: https://etherscan.io/address/0x694d4cFdaeE639239df949b6E24Ff8576A00d1f2
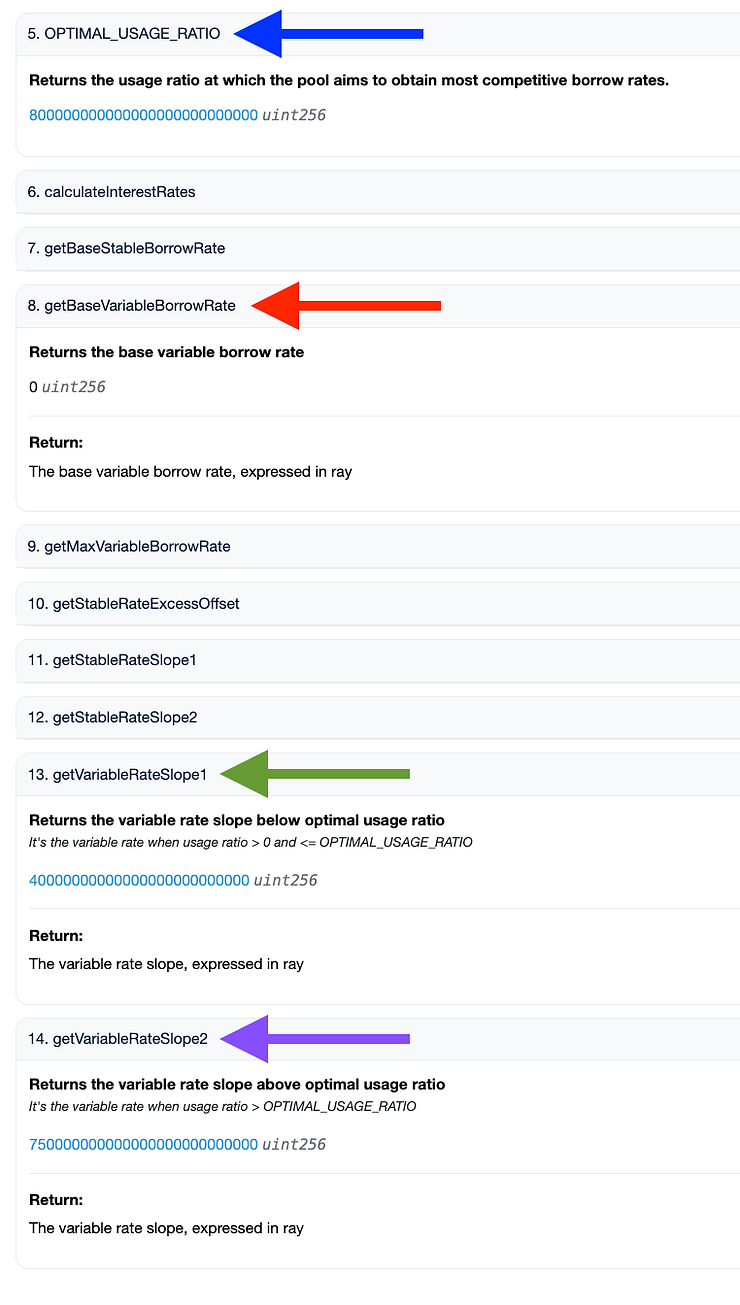
From the on-chain values, we can see that the following parameters were used in the interest-rate model:
- U_optimal ( blue arrow ) has the variable name OPTIMAL_USAGE_RATIO = 0.80
- R_intercept ( red arrow ) has the public function name getBaseVariableBorrowRate = 0
- R_slope1 ( green arrow ) has the public function name getVariableRateSlope1 = 0.04
- R_slope2 ( purple arrow ) has the public function name getVariableRateSlope2 = 0.75
The values are represented as fixed point Ray numbers (27 decimals, i.e. 1 = 1e27).
Parameters are accurate at time of writing.
Conclusion
Interest rates are a function of the utilization of the assets in the protocol. The exact shape of the function is set by governance. The interest suppliers earn is less than what the borrowers pay due to the spread and the reserve factor.
Learn More with RareSkills
Learn more technical topics in DeFi and web3 in our blockchain bootcamp.
Originally Published December 1, 2023