Tornado cash is a cryptocurrency smart contract mixer that enables users to deposit crypto with one address and withdraw with another wallet without creating a traceable link between those two addresses.
Tornado cash is probably the most iconic zero knowledge smart contract application, so we will explain how it works at a sufficiently low level that a programmer can reproduce the application.
It is assumed that the reader knows how Merkle Trees work and that inverting a cryptographic hash is infeasible. The reader is also assumed to be at least a strong intermediate at Solidity (since we will be reading snippets of the source code).
Tornado Cash is a fairly advanced smart contract, so check out our Solidity Tutorial first if you are still new to the language.
Tornado Cash is currently sanctioned by the United States government, interacting with it may “taint” your wallet and cause transactions from it to be flagged later when interacting with centralized exchanges.
On May 27, the Tornado Cash governance smart contracts (not the smart contracts we will review here) were hacked when an attacker passed a malicious proposal that gave them the majority of the ERC20 voting tokens for governance ERC20 voting tokens for governance. They have since handed back control, keeping a relatively small amount for themselves.
You can understand how Tornado Cash works without knowing zero knowledge proofs algorithms, but you must know how zero knowledge proofs work. Contrary to their name and many popular examples, Zero Knowledge Proofs prove the validity of a computation, not knowledge of a certain fact. They do not carry out the computation. They take an agreed-upon computation, a proof the computation was carried out, and the result of the computation, then determine if the prover really ran the computation and produced the output. The zero knowledge part comes from the optional feature that the proof-of-computation can be represented in a way that gives no information about the inputs.
For example, you can demonstrate you know the prime factors of a number without revealing them using the RSA algorithm. RSA doesn’t claim “I know two secret numbers” in isolation; it proves that you multiplied two concealed numbers together and generated the public number. RSA Encryption is really just a special case of zero knowledge proofs. In RSA, you demonstrate you know two secret primes that multiply together to produce your public key. In Zero Knowledge, you generalize that “magic multiplication” to arbitrary arithmetic and boolean operations. Once we have zero knowledge operations for elementary operations, we can build up zero knowledge proofs for more exotic things like proving we know the preimage of hash functions, Merkle roots, or even a fully functional virtual machine.
Another point: A zero knowledge proof verification does not carry out the computation, it only verifies someone carried out a computation and produced a claimed output.
Yet another useful corollary: To generate, but not verify, a zero knowledge proof of a computation, you must actually carry out the computation.
This makes sense right? How could you prove you know the preimage of a hash without actually hashing the preimage? Hence, the prover actually carries out the computation and creates some auxiliary data known as the proof to prove that they did the computation correctly.
When you validate an RSA signature, you don’t multiply someone else’s private key factors to produce their public key, that would defeat the purpose. You just verify the signature and the message checks out using a separate algorithm. Therefore, a computation consists of the following
verifier_algorithm(proof, computation, public_output) == true
In the context of RSA, you can think of the public key being the result of the computation, and the signature and message being the zero knowledge proof.
The computation and output are public. We agree that we are using a certain hash function and got a certain output. The proof “hides” the input that was used and only proves the hash function was executed and produced the output.
Given only the proof a verifier can not calculate the public_output. The verification step does not conduct the calculation, it only verifies that the claimed calculation that produces the public output based on the proof.
We aren’t going to teach zero knowledge algorithms in this article, but as long as you can accept that we can prove a computation took place without conducting the computation ourselves, we are good to go.
Fundamentally, Tornado Cash’s strategy for anonymization is mixing, similar to other anonymous cryptocurrencies like Monero. Multiple users submit their cryptocurrency to one address, “mixing” their deposits together. They then withdraw in such a way that the depositor and the withdrawer cannot be tied together.
Imagine 100 people put one dollar bills into a pile. Then 100 different people show up a day later and each withdraw a one dollar bill. In this scheme, we have no idea who the original depositors were trying to send the money to.
There is an obvious problem that if anyone could take the cash out of the pile, it will quickly get stolen. But if we try to leave some metadata behind about who is allowed to withdraw, then that will give away who the depositor is trying to send money to.
When you send Ether to Tornado Cash, this is fully public. When you withdraw from Tornado Cash, this is fully public too. What isn’t public is that the two addresses involved are associate with each other (assuming there are enough other depositors and withdrawers).
All people can tell about an address is “this address got its Ether from Tornado Cash” or “this other address deposited to Tornado Cash.” When an address withdraws from Tornado Cash, people can’t tell which depositor the crypto came from.
Let’s try to solve this problem without worrying about privacy.
The depositor creates two secret numbers, concatenates them, and puts the hash of it on chain when depositing the Eth (we will discuss later why we generated two secret numbers rather than one). When several people deposit, there are several public hashes sitting in a smart contract that we don’t know the preimage of.
The withdrawer shows up, the withdrawer reveals the preimage (the two secret numbers) of one of the hashes and takes their deposit out.
This clearly fails because it shows the depositor communicated to withdrawer the secret numbers off-chain.
However, if the withdrawer can demonstrate they know the preimage of one of the hashes without revealing which hash it is and without revealing the preimage of the hash, then we have a functional cryptocurrency mixer!
The naïve solution to this is to create a computation where we go over the hashes in a loop:
zkproof_preimage_is_valid(proof, hash_{1}) OR
zkproof_preimage_is_valid(proof, hash_{2}) OR
zkproof_preimage_is_valid(proof, hash_{3}) OR
...
zkproof_preimage_is_valid(proof, hash_{n-1}) OR
zkproof_preimage_is_valid(proof, hash_{n})
Remember, the verifier isn’t actually carrying out the above computation, so we don’t know which hash is the valid one. The verifier (tornado cash), is simply verifying the prover carried out the above computation and it returned true. How it returned true is irrelevant, only that it did; and it can only return true if the prover knows one of the preimages.
It is important to note at this point: all deposit hashes are publicly known. When a user deposits, they submit the hash of the two secret numbers, and that hash is public. What we are trying to conceal is which hash the withdrawer knows the preimage of.
But this is a very big computation. Big for-loops with a lot of deposits are expensive. [1]
We need a data structure that can compactly hold a lot of hashes in it, and thankfully we do: Merkle Trees.
Rather than looping over all the hashes, we can instead say “I know the preimage of one of the hashes” and “the hash is inside the Merkle Tree.” That accomplishes the same thing as pointing to a very long array of hashes and saying “I know the preimage of one of those hashes,” except it’s a lot more efficient.
Merkle Proofs are logarithmic in the size of the tree, so it doesn’t require too much extra work (compared to our massive for-loop from earlier).
When cryptocurrency is deposited, the user generates two secret numbers, concatenates them, hashes them, and puts the hash into the Merkle tree.
At withdraw time, the withdrawer produces a leaf hash preimage, then proves that leaf hash is in the tree via Merkle proof.
This of course ties the depositor to the withdrawer, but if we do both the Merkle proof and the leaf preimage verification in a zero knowledge manner, then the link is broken!
Zero knowledge proofs let us prove that we generated a valid Merkle proof against the public Merkle root as well as the preimage of the leaf – without showing how we conducted that computation.
It is not secure enough to simply provide an zero knowledge proof of having a Merkle proof and producing the root, the withdrawer must also prove they know the preimage of the leaf.
The Merkle Tree’s leaves are all public. Every time someone deposits, they supply a hash which is stored publicly. Since the Merkle tree is fully public, anyone can compute a Merkle proof for any of the leaves.
Therefore, proving a leaf is in the tree is not sufficient to prevent theft by proof forgery.
The withdrawer must also prove knowledge of the preimage of the leaf in question, without revealing the leaf. Remember, the leaf itself is the hash of two numbers.
You can see that the _commitment argument in the function for deposit is public. The _commitment variable is the leaf being added to the tree, which is the hash of the two secret numbers, which the depositor does not publish.
/**
@dev Deposit funds into the contract. The caller must send (for ETH) or approve (for ERC20) value equal to or `denomination` of this instance.
@param _commitment the note commitment, which is PedersenHash(nullifier + secret)
**/
function deposit(bytes32 _commitment) external payable nonReentrant {
require(!commitments[_commitment], "The commitment has been submitted");
uint32 insertedIndex = _insert(_commitment);
commitments[_commitment] = true;
_processDeposit();
emit Deposit(_commitment, insertedIndex, block.timestamp);
}
Effectively, the proof for withdrawal consists of proving the following computation has been carried out:
processMerkleProof(merkleProof, hash(concat(secret1, secret2))) == root
where processMerkleProof takes the Merkle proof and leaf as an argument, and hash(concat(secret1, secret2)) produces the leaf.
In the context of Tornado Cash, the verifier is the Tornado Cash smart contract that will release funds to whoever supplies a valid proof.
The prover is the withdrawer who can prove they carried out a hash computation to produce one of the leaves. Generally, the only person who can withdraw is the same person who deposited, as they would be the only party that can prove they know the hash preimages. Of course, this user must use a different and completely unassociated address for withdrawal!
The withdrawer actually caries out the above computation (Merkle proof and leaf hash generation), produces the zk-proof that they carried it out properly, then supplies this proof to the smart contract.
The merkleProof and {secret1, secret2} are hidden in the proof, but with the proof of computation, a verifier can validate the withdrawer actually ran the computation to correctly produce the leaf and Merkle root.
So let’s summarize:
The scheme above has an issue: what prevents us from withdrawing multiple times? Presumably, we’d have to “remove” the leaf from the Merkle Tree to account for the withdrawn deposit, but that would reveal which deposit is ours!
Tornado cash handles this by never removing leaves from the Merkle Tree. Once a leaf is added to the Merkle Tree, it stays there forever.
To prevent multiple withdrawals, the smart contract uses what is called a “nullifier scheme,” which is quite common in zero-knowledge applications and protocols.
A nullifier scheme in zero knowledge behaves like an exotic nonce that provides a layer of anonymity.
It will be clear why there are two secret numbers that make up a leaf, rather than one.
The two numbers that go into the deposit hash are the nullifier and a secret and the leaf is the hash of the concat(nullifier, secret) in that order.
During withdrawal, the user must submit the hash of the nullifier, i.e. the nullifierHash and proof they concatenated the nullifier and secret and hashed that to produce one of the leaves. The smart contract can then verify (using a zero knowledge algorithm) the sender really knows the preimage proof of the nullifier hash.
The nullifier hash is added to a mapping to ensure it is never reused.
This is why we need two secret numbers. If we revealed both numbers, then we would know which leaf the withdrawer was targeting! By revealing only one of the constituent numbers, it’s impossible to determine which leaf it is associated with.
Remember, zero knowledge proof verification cannot compute the nullifier given the secret input, it can only verify the computation, output, and proof are congruent. That is why the user must submit a public nullifierHash and proof they computed it from the hidden nullifier.
You can see this logic in the Tornado Cash withdraw function screenshotted below.
Let’s summarize. The user must prove
Here are the possible outcomes:
You may have noticed, we pulled a fast one in the above explanations. How can you update a Merkle Tree on chain without running out of gas? There are presumably a lot of deposits, and recomputing the whole thing would be prohibitive.
The incremental Merkle Tree gets around these restrictions with some clever optimizations. But before we get to the optimizations, we need to understand the restrictions.
An incremental Merkle Tree is a Merkle Tree of fixed depth where each leaf start as a zero value, and non-zero values are added by replacing the zero leaves starting from the left-most leaf to the right-most leaf one-by-one.
The animation below demonstrates an incremental Merkle Tree of depth 3, which can hold up to 8 leaves. In keeping with our domain terminology for Tornado Cash, we call these “commitments” labeled with the variable $C_i$.
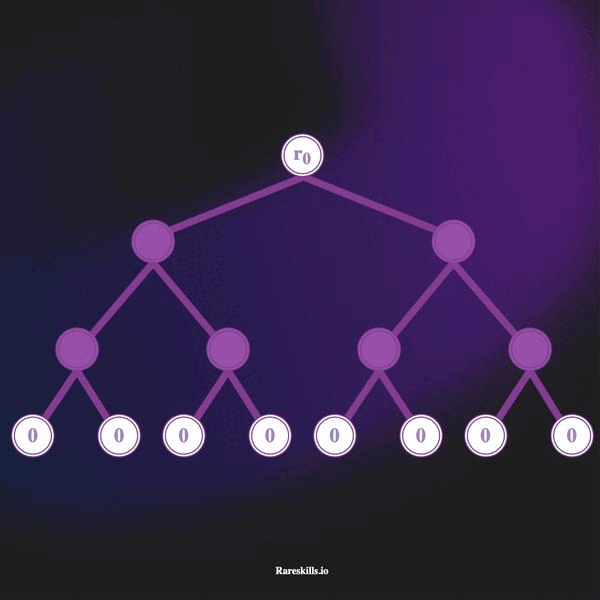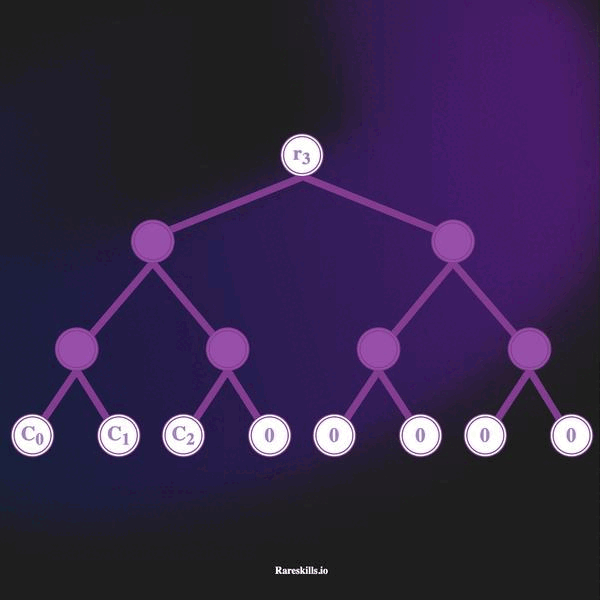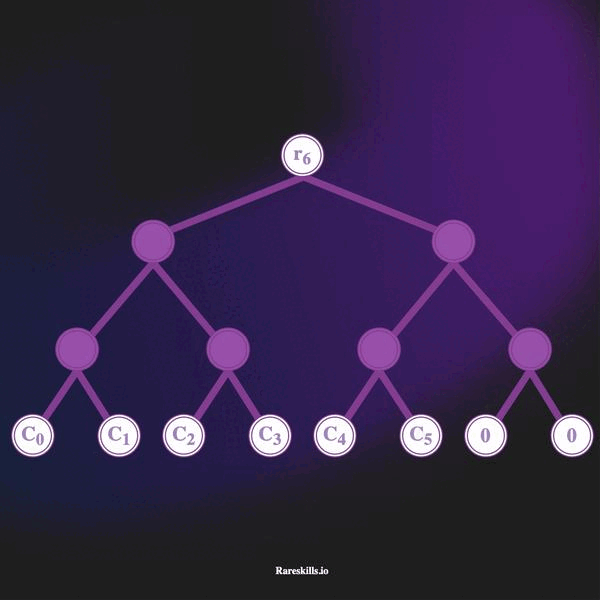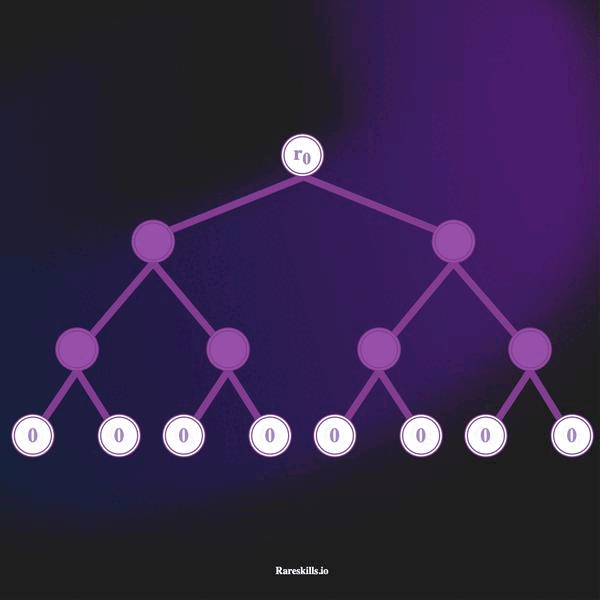
Here are some important features of an incremental Merkle tree
2^32 - 1 deposits. (This is an arbitrary depth chosen by Tornado Cash, but it needs to be constant).hash(bytes32(0)).Now we have a problem: building a Merkle Tree with 2^32 - 1 leaves on-chain is going to run out of gas. Just computing the first level will require over 4 million iterations, which obviously won’t work.
But restrictions of the incremental Merkle Trees enable two key invariants that allow the smart contract to take a big computational shortcut: every thing to the right of the current node is a Merkle subtrees of predictable height where all the roots are zero, and everything to the left of the current node can be cached instead of recomputed.
Since all of the leaves start off as zero, a significant amount of the work going into building the Merkle Tree will include computing Merkle Trees where all the leaves are zero.
See the image below and note how much computation is repeated when all the leaves are zero:
Most of the leaf-pairs are going to be the concatenation of bytes32(0) and bytes32(0). Then that hash is going to be concantenated with an identical hash from the sister subtree, and so forth and so on.
Tornado Cash pre-computes the hash of a depth-zero tree (just the hash of a bytes32(0) leaf), the root of a sub-tree with two leaves of zero, the root of a sub-tree with four leaves of zero, the root of a sub-tree with eight leaves of zero, and so forth.
This means we can precompute the Merkle root for a Merkle Tree (with all zero leaves) of height 0, 1, 2, etc until 31 (remember, the height of the Merkle Tree is fixed).
For each possible height of a Merkle subtree where the leaves are all zero, Tornado Cash precomputes it. Here is the precomputed list in Tornado Cash’s Merkle Tree With History:
/// @dev provides Zero (Empty) elements for a MiMC MerkleTree. Up to 32 levels
function zeros(uint256 i) public pure returns (bytes32) {
if (i == 0) return bytes32(0x2fe54c60d3acabf3343a35b6eba15db4821b340f76e741e2249685ed4899af6c);
else if (i == 1) return bytes32(0x256a6135777eee2fd26f54b8b7037a25439d5235caee224154186d2b8a52e31d);
else if (i == 2) return bytes32(0x1151949895e82ab19924de92c40a3d6f7bcb60d92b00504b8199613683f0c200);
else if (i == 3) return bytes32(0x20121ee811489ff8d61f09fb89e313f14959a0f28bb428a20dba6b0b068b3bdb);
else if (i == 4) return bytes32(0x0a89ca6ffa14cc462cfedb842c30ed221a50a3d6bf022a6a57dc82ab24c157c9);
else if (i == 5) return bytes32(0x24ca05c2b5cd42e890d6be94c68d0689f4f21c9cec9c0f13fe41d566dfb54959);
else if (i == 6) return bytes32(0x1ccb97c932565a92c60156bdba2d08f3bf1377464e025cee765679e604a7315c);
else if (i == 7) return bytes32(0x19156fbd7d1a8bf5cba8909367de1b624534ebab4f0f79e003bccdd1b182bdb4);
else if (i == 8) return bytes32(0x261af8c1f0912e465744641409f622d466c3920ac6e5ff37e36604cb11dfff80);
else if (i == 9) return bytes32(0x0058459724ff6ca5a1652fcbc3e82b93895cf08e975b19beab3f54c217d1c007);
else if (i == 10) return bytes32(0x1f04ef20dee48d39984d8eabe768a70eafa6310ad20849d4573c3c40c2ad1e30);
else if (i == 11) return bytes32(0x1bea3dec5dab51567ce7e200a30f7ba6d4276aeaa53e2686f962a46c66d511e5);
else if (i == 12) return bytes32(0x0ee0f941e2da4b9e31c3ca97a40d8fa9ce68d97c084177071b3cb46cd3372f0f);
else if (i == 13) return bytes32(0x1ca9503e8935884501bbaf20be14eb4c46b89772c97b96e3b2ebf3a36a948bbd);
else if (i == 14) return bytes32(0x133a80e30697cd55d8f7d4b0965b7be24057ba5dc3da898ee2187232446cb108);
else if (i == 15) return bytes32(0x13e6d8fc88839ed76e182c2a779af5b2c0da9dd18c90427a644f7e148a6253b6);
else if (i == 16) return bytes32(0x1eb16b057a477f4bc8f572ea6bee39561098f78f15bfb3699dcbb7bd8db61854);
else if (i == 17) return bytes32(0x0da2cb16a1ceaabf1c16b838f7a9e3f2a3a3088d9e0a6debaa748114620696ea);
else if (i == 18) return bytes32(0x24a3b3d822420b14b5d8cb6c28a574f01e98ea9e940551d2ebd75cee12649f9d);
else if (i == 19) return bytes32(0x198622acbd783d1b0d9064105b1fc8e4d8889de95c4c519b3f635809fe6afc05);
else if (i == 20) return bytes32(0x29d7ed391256ccc3ea596c86e933b89ff339d25ea8ddced975ae2fe30b5296d4);
else if (i == 21) return bytes32(0x19be59f2f0413ce78c0c3703a3a5451b1d7f39629fa33abd11548a76065b2967);
else if (i == 22) return bytes32(0x1ff3f61797e538b70e619310d33f2a063e7eb59104e112e95738da1254dc3453);
else if (i == 23) return bytes32(0x10c16ae9959cf8358980d9dd9616e48228737310a10e2b6b731c1a548f036c48);
else if (i == 24) return bytes32(0x0ba433a63174a90ac20992e75e3095496812b652685b5e1a2eae0b1bf4e8fcd1);
else if (i == 25) return bytes32(0x019ddb9df2bc98d987d0dfeca9d2b643deafab8f7036562e627c3667266a044c);
else if (i == 26) return bytes32(0x2d3c88b23175c5a5565db928414c66d1912b11acf974b2e644caaac04739ce99);
else if (i == 27) return bytes32(0x2eab55f6ae4e66e32c5189eed5c470840863445760f5ed7e7b69b2a62600f354);
else if (i == 28) return bytes32(0x002df37a2642621802383cf952bf4dd1f32e05433beeb1fd41031fb7eace979d);
else if (i == 29) return bytes32(0x104aeb41435db66c3e62feccc1d6f5d98d0a0ed75d1374db457cf462e3a1f427);
else if (i == 30) return bytes32(0x1f3c6fd858e9a7d4b0d1f38e256a09d81d5a5e3c963987e2d4b814cfab7c6ebb);
else if (i == 31) return bytes32(0x2c7a07d20dff79d01fecedc1134284a8d08436606c93693b67e333f671bf69cc);
else revert("Index out of bounds");
}
When computing the Merkle root, we always know the “z-level” we are at and can simply get the precomputed Merkle subtree root where all the leaves are zero.
Tornado cash doesn’t actually use the hash(bytes32(0)) as the empty value, it uses hash(“tornado”). This doesn’t affect the algorithm, as it is just a constant. However, it’s easier to discuss Incremental Merkle Trees using a notion of zeroness being zero rather than a funny constant.
Consider the case where we add the second deposit. We’ve already computed the hash of the first deposit. That hash gets cached in a mapping Tornado Cash calls filledSubtrees. A filledSubtree is simply a subtree in the Merkle Tree where all of the leaves are non-zero. We call that fs in the animation below:
The point is, any time you need an intermediate hash on the left, it’s already been computed for you.
This nice feature is a byproduct of the restriction that leaves cannot be changed or removed. Once a subtree is full of commitments instead of zeros, it never needs to be recomputed.
Now let’s generalize this. Instead of seeing the node to our left as the “first deposit”, imagine that itself is the root of a subtree.
In the most extreme case, consider when we put in the very last leaf. To our immediate left will be a “tree” that consists of the second-to-last leaf (depth 0), to that left will be a subtree of depth 1, to that left will be a subtree of depth 2 (with 4 leaves), to that left will be a subtree of depth 3 (with 8 leaves), etc. There won’t be more than 32 such trees in the most extreme case.
Everything to our left is a filled subtree (even if it is just a leaf) and everything to our right is always a zero leaf or a subtree that consists of all zero leaves. Since the left root is cached, and the right root is precomputed from a subtree of height $n$ of all zeros, we can compute any intermediate hash concatenation at any level efficiently, and generate a depth-32 Merkle Tree on chain with only 32 iterations. This isn’t cheap, but it’s feasible. It sure is a lot better than 4 million computations though!
But as we “hash our way to the root”, how do we know which order to concatenate the hashes of the subtrees?
For example, we take a new commitment hash and add it as a leaf. In the node above us, do we concatenate it as new_commitment | other_value or other_value | new_commitment?
Here is the trick: every even indexed node is a left child, and every odd indexed node is a right child. This is true for the leaf nodes and for every level of the tree. You can see this pattern in the diagram below.
Let’s get an intuition for the pattern. If the zeroth leaf is being inserted, then we are only going to hash right on the way to the root. 0 ÷ 2 will remain zero, and zero is an even number using the definition above. Because zero is even, we will always hash right on our way to the root.
Now let’s look at the other extreme case. When the last leaf is inserted, one must always hash left on the way to the root. Every node on the way to the top is odd. This pattern generalizes to every node in the middle; starting with the index of the leaf and repeatedly dividing by two as we go up the tree will tell us if we are on a left child or on a right child. The following animation illustrates that we hash left when we are on an odd node and hash right when we are on an even node:
So at any level, we know where are hash goes in relation to the sibling.
Hence, there are two pieces of information we need:
Here is a screenshot of Tornado Cash’s source code using that information. The for loop loops over the levels to regenerate the Merkle root based on the new leaf that was just added.
In summary, to update the Merkle Root on-chain, we
currentIndexcurrentIndex to be currentIndex divided by two. Then,filledSubtree if the currentIndex is oddprecomputed zero-tree if the currentIndex is even.It’s quite cool that such a non-trivial algorithm can be compressed to a small Solidity representation.
Whenever an item is inserted, the Merkle root must necessarily change. This could create a problem if a withdrawer creates a Merkle proof for the latest root (remember, the leaves are all publicly available) but a deposit transaction comes in first and changes the root; then the Merkle proof would no longer be valid. The zk verifier algorithm ensures the proof of the Merkle proof is valid for the root, so if the root changes, the proof won’t check out.
To give the withdrawer time to withdraw their transaction, they can refer to up to the last 30 roots.
The variable roots is a mapping from uint256 to bytes32. When the Merkle proof has reached the root (the loop completes) it is stored in roots. The currentRootIndex is increased up to the ROOT_HISTORY_SIZE, but once it reaches the maximum value (30) it overwrites the root in index zero. Thus, it behaves like a fixed size queue. Below is a snippet from the _insert function of Tornado Cash’s Merkle Tree code. After the root is recomputed, it is stored in the manner described above.
Here are the storage variables needed for the Merkle Tree with history to work.
mapping(uint256 => bytes32) public filledSubtrees;
mapping(uint256 => bytes32) public roots;
uint32 public constant ROOT_HISTORY_SIZE = 30;
uint32 public currentRootIndex = 0;
uint32 public nextIndex = 0;
filledSubtrees is the subtrees we have already computed (i.e. all the leaves are non-zero)currentRootIndex is a number from 0 to 29 to index into rootsnextIndex is the current leaf that will be filled if the user calls Deposit.When a user calls deposit to tornado cash, _insert() is called to update the Merkle Tree, and _processDeposit() is called afterwards.
function deposit(bytes32 _commitment) external payable nonReentrant {
require(!commitments[_commitment], "The commitment has been submitted");
uint32 insertedIndex = _insert(_commitment);
commitments[_commitment] = true;
_processDeposit();
emit Deposit(_commitment, insertedIndex, block.timestamp);
}
_processDeposit() just makes sure the denomination is accurate (you can only deposit 0.1, 1, or 10 Ether depending on which Tornado Cash instance you interact with). The code for that very simple operation is below.
function _processDeposit() internal override {
require(msg.value == denomination, "Please send `mixDenomination` ETH along with transaction");
}
To compute the Merkle root on-chain, one must use a hash algorithm (obviously) but Tornado cash isn’t using the traditional keccak256; it uses MiMC instead.
Why this is so is a bit out of scope, but the reason is that some hashes are more computationally cheap for zero knowledge proof generation than others. MiMC was designed to be “zk friendly” but keccak256 was not.
“Zk friendly” means the algorithm maps naturally to how zero knowledge proof algorithms represents computations.
But this creates a funny conundrum that the MiMC must be computed on-chain to recompute the root when a new node is added, and Ethereum does not have precompiled contracts for zk-friendly hashes. (Maybe you could author an EIP for this?)
Therefore, the Tornado Cash team wrote it themselves in raw bytecode. If you look at the Etherscan contract verification for Tornado Cash, you will see a warning:
Etherscan cannot verify raw bytecode to Solidity, since the MiMC hash was not written in Solidity.
The Tornado Cash team deployed the MiMC Hasher as a separate smart contract. To use the MiMC hash, the Merkle Tree Code makes a cross contract call to that contract. As you can see in the code below, these are static calls, since the interface defines it as pure, hence Etherscan shows it as having no transaction history.
interface IHasher {
function MiMCSponge(uint256 in_xL, uint256 in_xR) external pure returns (uint256 xL, uint256 xR);
}
We know it’s “interface” based on the code in Tornado cash referenced above. (github link).
On a circom library github issue, you can see the justification for why the code does not have a solidity version, even with assembly blocks: direct stack manipulation isn’t possible.
(Sidenote: very low level cryptography algorithms are a fantastic usecase for the Huff Language, which you can learn with our Huff Language Puzzles).
The circomlib js repository contains javascript tooling for creating raw bytecode hashes. Here is the code for generating MiMC and the Poseidon Hash.
To start, the user must reconstruct the Merkle Tree locally using the updateTree script. This script will download all the relevant solidity events and reconstruct the Merkle Tree. Then, the user will generate a zero knowledge proof of the Merkle proof and leaf commitment preimages. As discussed earlier, Tornado Cash stores the last 30 Merkle roots, so this should be plenty of time for the user to submit their proof. If a user generates a proof and waits too long, they will have to regenerate the proof.
The tornado cash contract will check
nullifierHash hasn’t been used beforenullifierHash preimage
c. The user created a Merkle proof using that leaf which results in the proposed root.
d. The proposed root is one of the last 30 roots (this is checked publicly in the Solidity code)Here is a visualization of the above steps:
With that understanding, the code from Tornado Cash’s withdraw function below should be self explanatory.
function withdraw(bytes calldata _proof,
bytes32 _root,
bytes32 _nullifierHash,
address payable _recipient,
address payable _relayer,
uint256 _fee,
uint256 _refund
) external payable nonReentrant {
require(_fee <= denomination, "Fee exceeds transfer value");
require(!nullifierHashes[_nullifierHash], "The note has been already spent");
require(isKnownRoot(_root), "Cannot find your merkle root"); // Make sure to use a recent onerequire(
verifier.verifyProof(
_proof,
[uint256(_root), uint256(_nullifierHash), uint256(_recipient), uint256(_relayer), _fee, _refund]
),
"Invalid withdraw proof"
);
nullifierHashes[_nullifierHash] = true;
_processWithdraw(_recipient, _relayer, _fee, _refund);
emit Withdrawal(_recipient, _nullifierHash, _relayer, _fee);
}
The _relayer, _fee, and _refund above has to do with paying fees to optional transaction relayers, which we will explain shortly.
This is a simple do-while loop that loops backwards from the current index (the last active leaf) to see if the root submitted to the withdraw function is in the history of roots. (github link)
Because there is a lookback of only 30, we don’t have to worry about unbounded loops using up too much gas.
/**
@dev Whether the root is present in the root history
*/function isKnownRoot(bytes32 _root) public view returns (bool) {
if (_root == 0) {
return false;
}
uint32 _currentRootIndex = currentRootIndex;
uint32 i = _currentRootIndex;
do {
if (_root == roots[i]) {
return true;
}
if (i == 0) {
i = ROOT_HISTORY_SIZE; // 30
}
i--;
} while (i != _currentRootIndex);
return false;
}
This section describes the circom code used to generate the circuits that verify the ZK proof. If you are unfamiliar with Circom and want to learn it, please check out our zero knowledge puzzles in Circom.
Nevertheless, we will still try to explain the Circom code at a high level.
Circom is not executed on the blockchain, it is transpiled into terrifying Solidity code which you can see in Tornado Cash’s Verifier.sol . The reason it looks so scary is that it is actually executing the math for the zk-proof verification. Thankfully, Circom is a lot more readable.
Here we have three components: HashLeftRight which combines hashes, DualMux (which is just a utility for MerkleTreeChecker) and MerkleTreeChecker. The MerkleTreeChecker takes a leaf, a root, and a proof. The proof has two parts: the pathElements (the Merkle root of the sister subtree) and pathIndices (and indicator for the circuit to know which order to concatenate the hashes for that level).
The final line, root === hashers[levels - 1].hash is where the root is finally determined to match the leaf and proof.
Recall that the nullifierHash is the hash of the nullifier and the commitment is the hash of the nullifier and the secret. The Circom representation of this calculation is below. Although it may be hard to read, it should be clear that the inputs are the nullifier and secret, and the outputs are the commitment and the nullifierHash.
Now we can get to the core of the zero knowledge algorithm
A private signal means it is “hidden in the proof” using the nomenclature from earlier.
In the code above, the code verifies the nullifier hash computation was conducted in a valid manner. Then the commitment preimage and Merkle proof are provided to the MerkleTree Verifier from earlier.
If everything checks out, the verifier will return true, denoting the proof is valid, and the anonymous address can withdraw the deposit.
Security researchers may have noticed the Solidity code has no defense against frontrunning. When someone submits a valid zero knowledge proof to the mempool, what prevents someone from copying the proof and substituting the withdraw address to be their own?
This is something we glossed over for simplicity, but the Withdraw.circom file includes dummy signals that square the recipient (and the other parameters needed for relayers). This means the zk-proof must also demonstrate that the withdrawer squared the recipient’s address and got the square of their address (remember, addresses are just 20 byte numbers). Computing the square of the addresses and the hash of the nullifier and secret is one computation, so getting any parts of this wrong invalidates the whole proof.
A relayer is an offchain bot that pays the gas for other users in exchange for some kind of payment. Tornado Cash withdrawers generally want to use completely new addresses to enhance privacy, but completely new addresses don’t have any gas to pay for the withdrawal.
To solve this, a withdrawer can ask a relayer to conduct the transaction in exchange for receiving a portion of the Tornado Cash withdrawal.
The relayer’s withdraw address must also use the same frontrunning protection described above, and that can be seen in the code screenshot above.
When deposit is called:
hash(concat(nullifier, secret)), along with the cryptocurrency they are depositing.When withdraw is called:
nullifier (publicly), the Merkle root they are verifying against, and a zk proof that they know the nullifier, secret, and Merkle proofnullifier hasn’t been used beforeThere is nothing stopping a user from submitting a nonsense leaf with no known preimage. In that case, the submitted cryptocurrency will remain stuck in the contract forever.
The following are the smart contracts that make up Tornado Cash
Tornado.sol is an abstract contract that is actually implemented by ERC20Tornado.sol or ETHTornado.sol depending on if the deployment is meant to mix ERC20s or a certain denomination of ETH. Different ETH denominations and ERC20 tokens have their own tornado cash instance.
MerkleTreeWithHistory.sol contains the _insert() and isKnownRoot() functionality we discussed at length earlier.
Verifier.sol is the Solidity transpilation output of the Circom circuits.
cTornado.sol is the ERC20 token for governance, and isn’t part of the core protocol.
Tornado Cash overall is very well architected, but there are a few opportunities for gas optimization.
nullifierHashes is a public mapping, but it also wrapped with a public view function isSpent(). This is redundant.And there you have it; we have surveyed the entire codebase of Tornado Cash and developed a good understanding of what each variable and function does. Tornado Cash packs an impressive amount of complexity into a relatively small codebase. We’ve looked at several nontrivial techniques here including:
This material is part of our Zero Knowledge Course. For general smart contract development, see our Solidity Bootcamp for professional Solidity developers. We offer the most rigorous and up-to-date training program for smart contracts available anywhere.
[1] Anyone familiar with ZK circuits knows we cannot create for loops of arbitrary length. The circuit must be built to accommodate very large arrays when it is created. However, it is still accurate to say that “looping” over that many hashes is computationally expensive, as it is equivalent to creating an infeasibly massive circuit.
Originally Published June 27, 2023
get_D() and get_y() in Curve StableSwap This article shows algebraically step-by-step how the code for get_D() and get_y() are derived from the StableSwap invariant. Given the StableSwap Invariant: $$ An^n\sum x_i +D=An^nD+\frac{D^{n+1}}{n^n\prod x_i} $$ There are two frequent math operations we wish to conduct with it: Compute $D$ given fixed values for $A$, and the […]
20 Common Solidity Beginner Mistakes Our intent is not to be patronizing towards developers early in their journey with this article. Having reviewed code from numerous Solidity developers, we’ve seen some mistakes occur more frequently and we list those here. By no means is this an exhaustive list of mistakes a Solidity developer can make. […]
The intuition behind elliptic curve digital signatures (ECDSA) This article explains how the ECDSA (Elliptic Curve Digital Signature Algorithm) works as well as why it works. We will incrementally “rediscover” the algorithm from first principles in this tutorial. Prerequisites We assume prior knowledge of Elliptic Curve Arithmetic Elliptic Curve Arithmetic in Finite Fields Digital Signature […]
Smart Contract Foundry Upgrades with the OpenZeppelin Plugin Upgrading a smart contract is a multistep and error-prone process, so to minimize the chances of human error, it is desirable to use a tool that automates the procedure as much as possible. Therefore, the OpenZeppelin Upgrade Plugin streamlines deploying, upgrading and managing smart contracts built with Foundry or […]