This article explains how the getSqrtRatioAtTick() function in Uniswap V3 TickMath library works. The getSqrtRatioAtTick() function takes a tick index and returns the square root price at that exact tick as a Q64.96 q-number. The function computes:
where is the tick index. Below is a screenshot of the function:
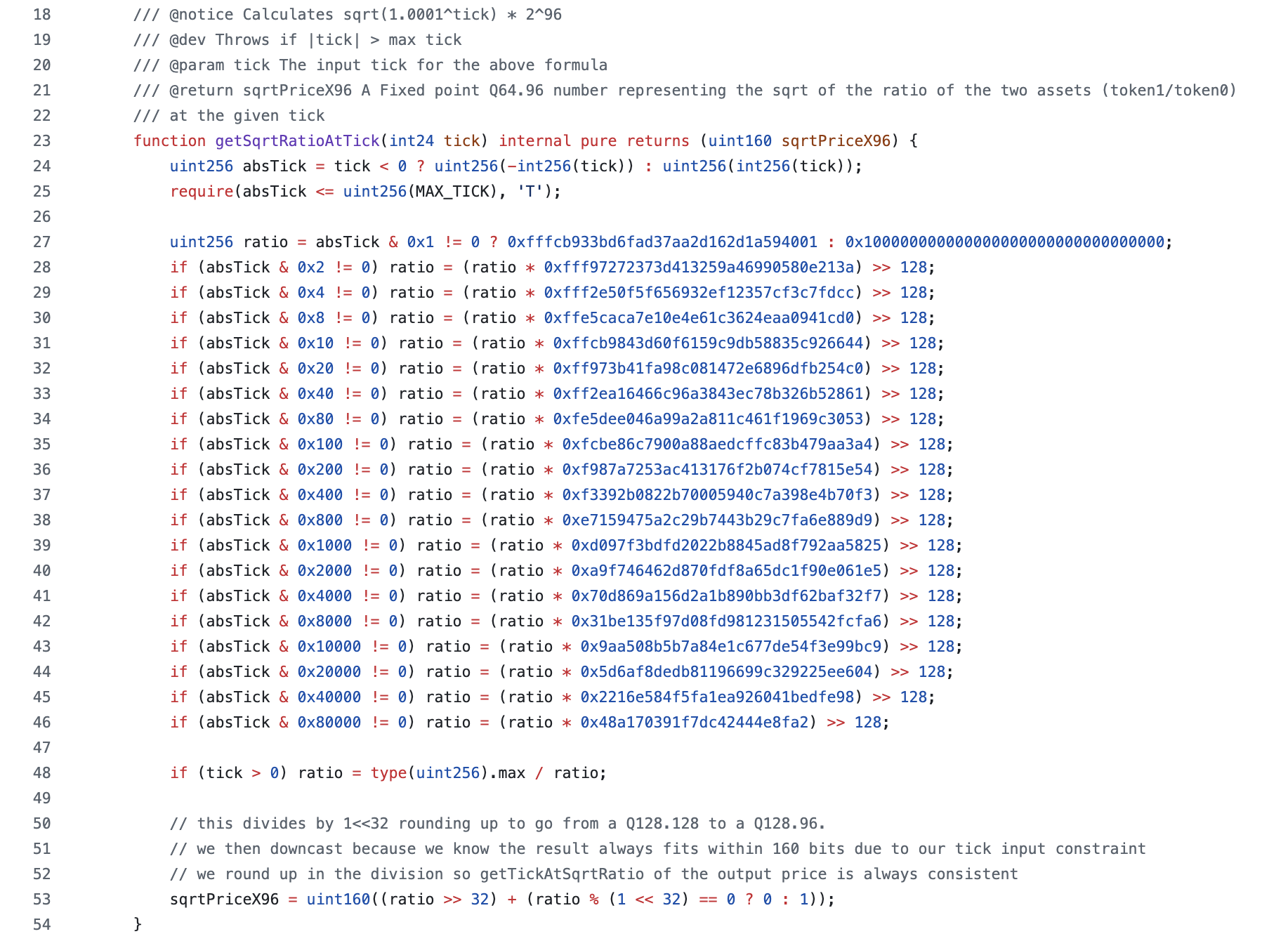
This tutorial assumes the reader has understood our treatment of the square-and-multiply algorithm, which getSqrtRatioAtTick() relies on. We refer to concepts in that tutorial regularly here, so we suggest the reader review that article first.
getSqrtPriceRatioAtTick overview
The function takes the following steps:
- Compute the absolute value of the tick with the code
uint256 absTick = tick < 0 ? uint256(-int256(tick)) : uint256(int256(tick));. - Check that the tick falls in the range of the minimum and maximum tick and revert if out of range:
require(absTick <= uint256(MAX_TICK), 'T');. - Compute as a Q128.128 number using square-and-multiply.
- If the original tick was positive, compute
- Convert the Q128.128 number to a Q64.96 number with
>> 32
Here are the steps outlined in the code:
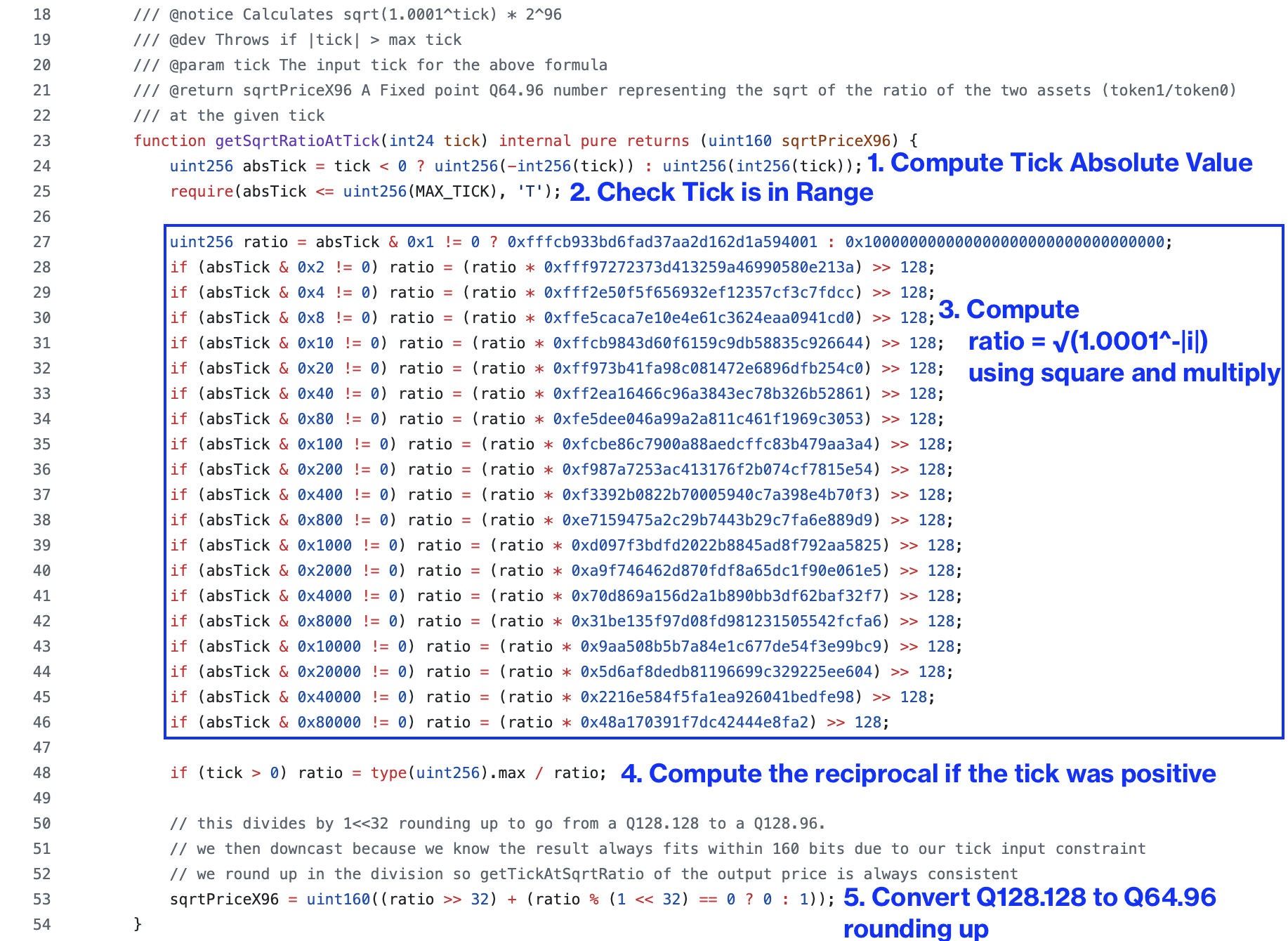
Part 1/5: Why Uniswap V3 computes absolute value tick, i.e.
The first line of code in the function computes the absolute value of the tick:
uint256 absTick = tick < 0 ? uint256(-int256(tick)) : uint256(int256(tick));
Tick indices can be both positive and negative. To avoid handling both cases separately, the square-and-multiply portion of getSqrtRatioAtTick() only computes negative ticks. If the original tick was positive, then the result of the square-and-multiply algorithm computes the reciprocal.
For example, if the original tick is tick positive 5, the algorithm computes the tick for -5:
Then computes the reciprocal:
Observe that in general:
Therefore, the function first computes:
Then, if the tick was originally positive, it inverts the answer by returning the reciprocal:
If the tick was originally negative, the code does not compute the reciprocal.
Part 2/5: Checking if the tick is in range
The second line of code in the function is self explanatory:
require(absTick <= uint256(MAX_TICK), 'T');
Max tick is a constant 887272 ******in the file which we derived in our article on Tick Limits. We don’t need to check if the tick is less than MIN_TICK since we computed the absolute value of the tick, so absTick cannot be negative.
Part 3/5: Computing the price using square and multiply
In this section, we show how the function is using the square and multiply algorithm and derive the large constants in the function.
The variable used for computing the price is ratio but the variable returned is sqrtPriceX96.
Here is the relevant part of the function that uses square and multiply:
uint256 ratio = absTick & 0x1 != 0 ? 0xfffcb933bd6fad37aa2d162d1a594001 : 0x100000000000000000000000000000000;
if (absTick & 0x2 != 0) ratio = (ratio * 0xfff97272373d413259a46990580e213a) >> 128;
if (absTick & 0x4 != 0) ratio = (ratio * 0xfff2e50f5f656932ef12357cf3c7fdcc) >> 128;
if (absTick & 0x8 != 0) ratio = (ratio * 0xffe5caca7e10e4e61c3624eaa0941cd0) >> 128;
if (absTick & 0x10 != 0) ratio = (ratio * 0xffcb9843d60f6159c9db58835c926644) >> 128;
if (absTick & 0x20 != 0) ratio = (ratio * 0xff973b41fa98c081472e6896dfb254c0) >> 128;
if (absTick & 0x40 != 0) ratio = (ratio * 0xff2ea16466c96a3843ec78b326b52861) >> 128;
if (absTick & 0x80 != 0) ratio = (ratio * 0xfe5dee046a99a2a811c461f1969c3053) >> 128;
if (absTick & 0x100 != 0) ratio = (ratio * 0xfcbe86c7900a88aedcffc83b479aa3a4) >> 128;
if (absTick & 0x200 != 0) ratio = (ratio * 0xf987a7253ac413176f2b074cf7815e54) >> 128;
if (absTick & 0x400 != 0) ratio = (ratio * 0xf3392b0822b70005940c7a398e4b70f3) >> 128;
if (absTick & 0x800 != 0) ratio = (ratio * 0xe7159475a2c29b7443b29c7fa6e889d9) >> 128;
if (absTick & 0x1000 != 0) ratio = (ratio * 0xd097f3bdfd2022b8845ad8f792aa5825) >> 128;
if (absTick & 0x2000 != 0) ratio = (ratio * 0xa9f746462d870fdf8a65dc1f90e061e5) >> 128;
if (absTick & 0x4000 != 0) ratio = (ratio * 0x70d869a156d2a1b890bb3df62baf32f7) >> 128;
if (absTick & 0x8000 != 0) ratio = (ratio * 0x31be135f97d08fd981231505542fcfa6) >> 128;
if (absTick & 0x10000 != 0) ratio = (ratio * 0x9aa508b5b7a84e1c677de54f3e99bc9) >> 128;
if (absTick & 0x20000 != 0) ratio = (ratio * 0x5d6af8dedb81196699c329225ee604) >> 128;
if (absTick & 0x40000 != 0) ratio = (ratio * 0x2216e584f5fa1ea926041bedfe98) >> 128;
if (absTick & 0x80000 != 0) ratio = (ratio * 0x48a170391f7dc42444e8fa2) >> 128;
ratio is a Q128.128 but sqrtPriceX96 is a Q64.96
To maximize precision, getSqrtRatioAtTick() internally uses Q128.128 numbers while carrying out the square-and-multiply algorithm, but returns the answer as a Q64.96. The internal representation of the price is the ratio variable.
Square-and-multiply precomputation review
In order to explain how Uniswap V3 derived the large constants shown above, we must first review the square and multiply algorithm.
The square-and-multiply algorithm relies on precomputing powers of the base. We now show that the large constants in the code are derived from repeatedly squaring .
Using the square-and-multiply algorithm, getSqrtRatioAtTick() precomputes
The minimum and maximum ticks in Uniswap V3 are -887,272 and 887,272 respectively. However, since getSqrtPriceRatioAtTick only computes the negative portion directly, and compute the positive ticks by reciprocal, it only needs to compute ticks [-887,272,0]. The number of bits required to encode a number up to 887,273 (887,272 plus 0) is 20 since . This is why the precomputed values range from , ,…, .
As an example, suppose we want to compute the price at tick -100. We can multiply the precomputed values for tick -64, -32, and -4 as follows:
Deriving the large constant values as Q128.128 numbers
We now show how Uniswap V3 derived the large constants.
Square root price of tick 0
The large constant 0x100000000000000000000000000000000 (purple box) is the Q128.128 fixed point number (equivalent to 2 << 128).
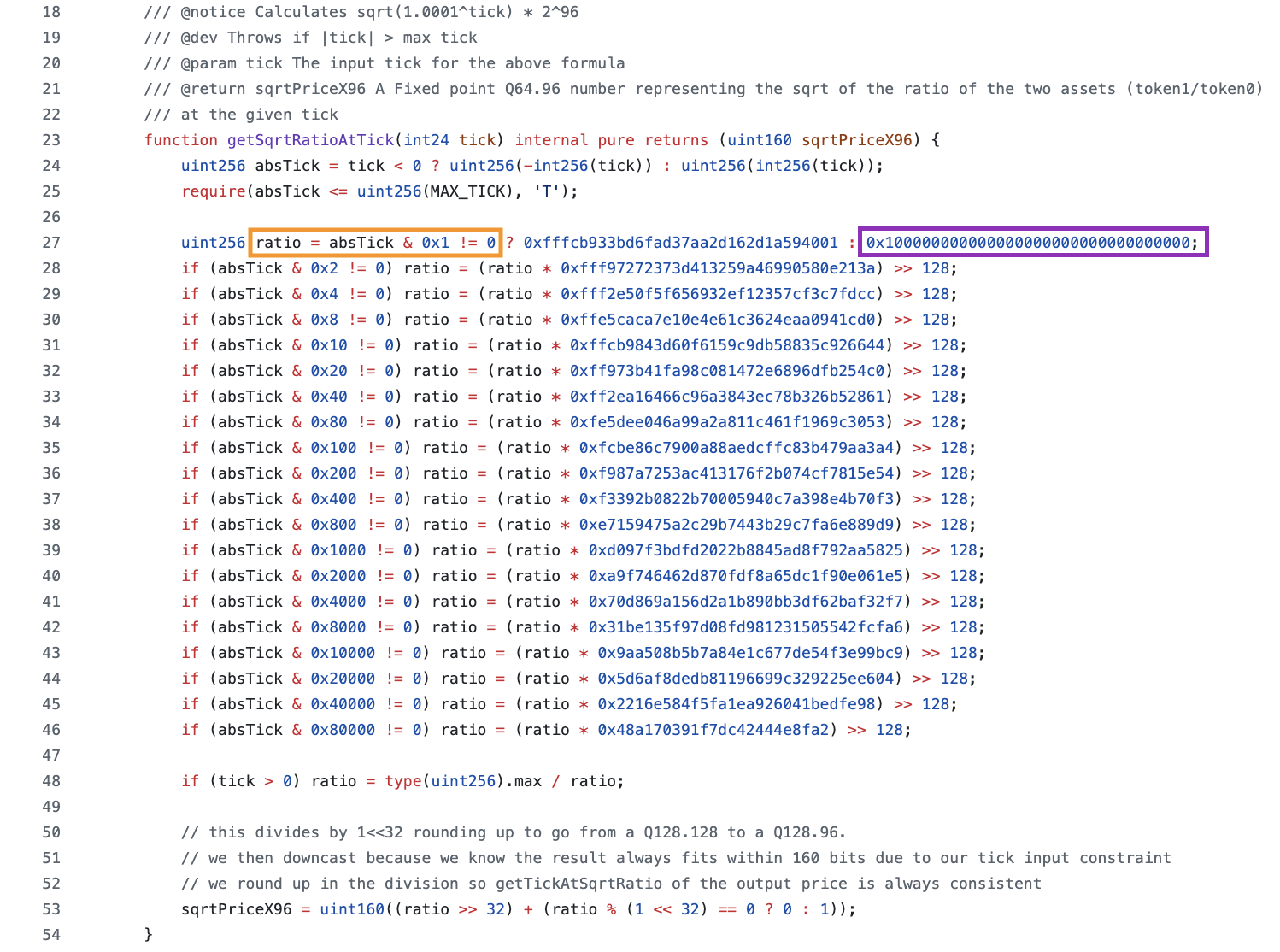
This corresponds to tick 0, . Consider that if tick = 0, then absTick & 0x1 != 0 one line 27 (orange box) will be false, triggering the second part of the ternary operator.
If this tick is 0, none of the other bits will be 1 and hence none of the subsequent conditionals if (absTick & 0xXX !=0) will be true, meaning that ratio will be equal to 0x100000000000000000000000000000000 with no further modifications. This is expected, since raising a number to zero returns 1.
Square root price of tick -1
If we compute the price of tick -1 in Q128.128 in Python we get the following:
>>>
0xfffcb933bd6f b0000000000000000000 # gap added for clarity
When converted to hex, it is close to the magic number highlighted below, but it is clear our estimate above has more zeros at the end, meaning it had precision loss:
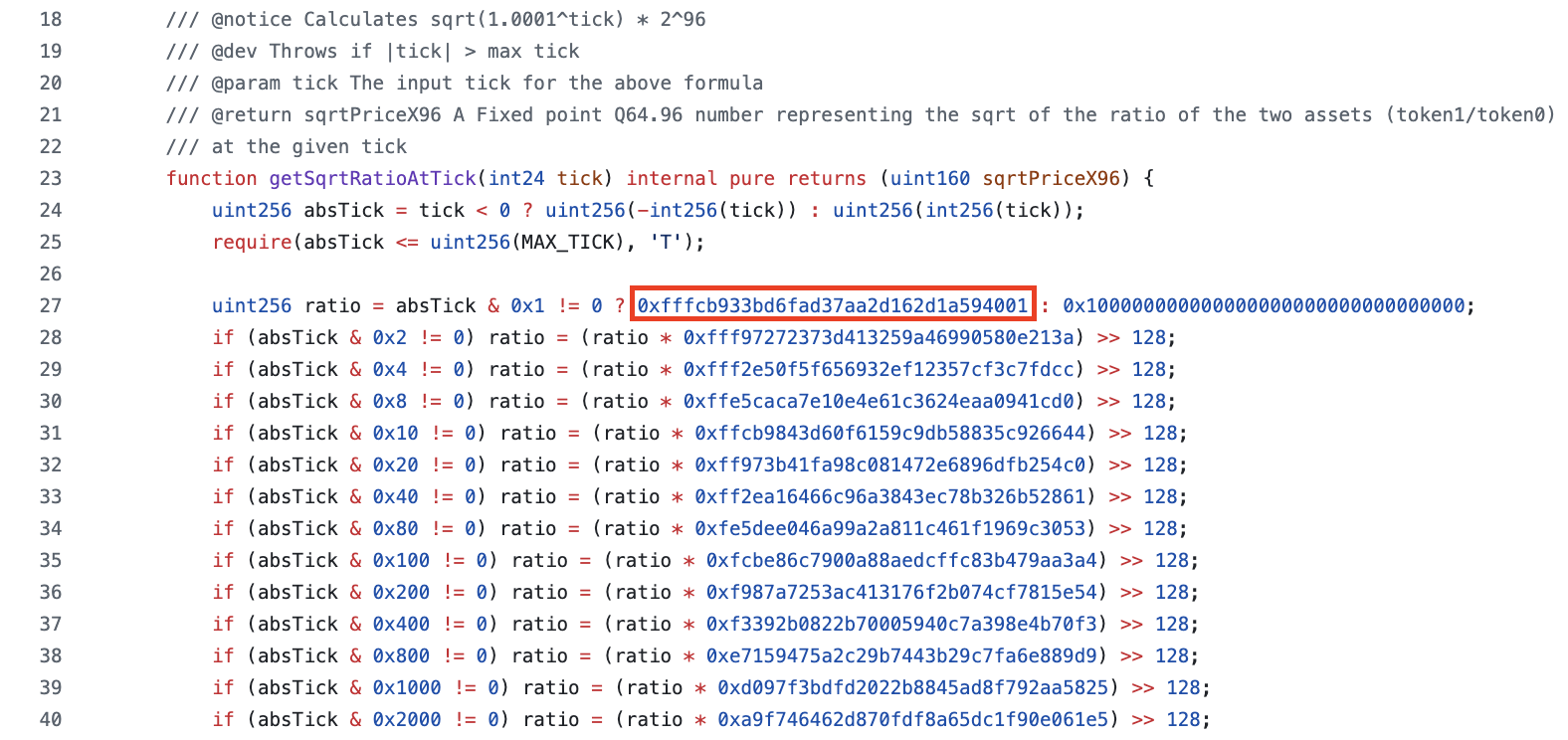
Here is Uniswap’s constant for compared to our estimate:
# Uniswap's constant
>>> hex(0xfffcb933bd6fad37aa2d162d1a594001)
0xfffcb933bd6f ad37aa2d162d1a594001 # gap added for clarity
# Our constant
>>> hex(int(2**128 * math.sqrt(1.0001**-1)))
0xfffcb933bd6f b0000000000000000000 # gap added for clarity
# note that Uniswap's and our estimate differ after the gap
In the next section, we show how to improve our estimate to match Uniswap V3’s.
Improving our constant calculations by using Decimal and re-arranging divisions
By default, Python floats do not have enough precision to compute numbers with 128 bits of precision, but we fix that by using the Decimal library which gives us as much precision as we want:
from decimal import *
getcontext().prec = 100 # use 100 decimals of precision is ~333 bits
Furthermore, to eliminate imprecision involving decimals, we can compute
as
This eliminates the fraction 1.0001.
We can improve the precision again by avoiding negative exponents (which have implied division). Observe we can get rid of the negative exponents by flipping the numerator and denominator:
Looking ahead to tick -2, instead of computing Decimal(10001)**Decimal(-2/2) (or ) for the second negative tick, we directly simplify it to Decimal(10001)**Decimal(-1) to minimize introducing division operations where they aren’t needed.
With that change, we can now more accurately reproduce the Uniswap V3 precomputed values. The values below are multiplied by 2**128 to turn them into fixed-point numbers:
from decimal import *
getcontext().prec = 100
# tick -1
print(hex(int(Decimal(10000)**Decimal(1/2) * 2**128 / Decimal(10001)**Decimal(1/2))))
# estim: 0xfffcb933bd6fad37aa2d162d1a594001
# uniV3: 0xfffcb933bd6fad37aa2d162d1a594001
# tick -2
print(hex(int(Decimal(10000)**Decimal(1) * 2**128 / Decimal(10001)**Decimal(1))))
# estim: 0xfff97272373d413259a46990580e2139
# uniV3: 0xfff97272373d413259a46990580e213a
# tick -4
print(hex(int(Decimal(10000)**Decimal(2) * 2**128 / Decimal(10001)**Decimal(2))))
# estim: 0xfff2e50f5f656932ef12357cf3c7fdcb
# uniV3: 0xfff2e50f5f656932ef12357cf3c7fdcc
# tick -8
print(hex(int(Decimal(10000)**Decimal(4) * 2**128 / Decimal(10001)**Decimal(4))))
# estim: 0xffe5caca7e10e4e61c3624eaa0941ccf
# uniV3: 0xffe5caca7e10e4e61c3624eaa0941cd0
# tick -16
print(hex(int(Decimal(10000)**Decimal(8) * 2**128 / Decimal(10001)**Decimal(8))))
# estim: 0xffcb9843d60f6159c9db58835c926643
# univ3: 0xffcb9843d60f6159c9db58835c926644
Note that our computation of the constants in the code above is just shy of the actual code values by 1, which means that Uniswap V3 is rounding up the decimal to obtain its constants.
In conclusion, each of the “magic numbers” in getSqrtRatioAtTick() are the following numbers represented as a 128-bit fixed point number rounded up (except tick 1).
Part 4/5: Computing the reciprocal with Q128.128 numbers
The line of code shown below computes the reciprocal if the original tick was positive.
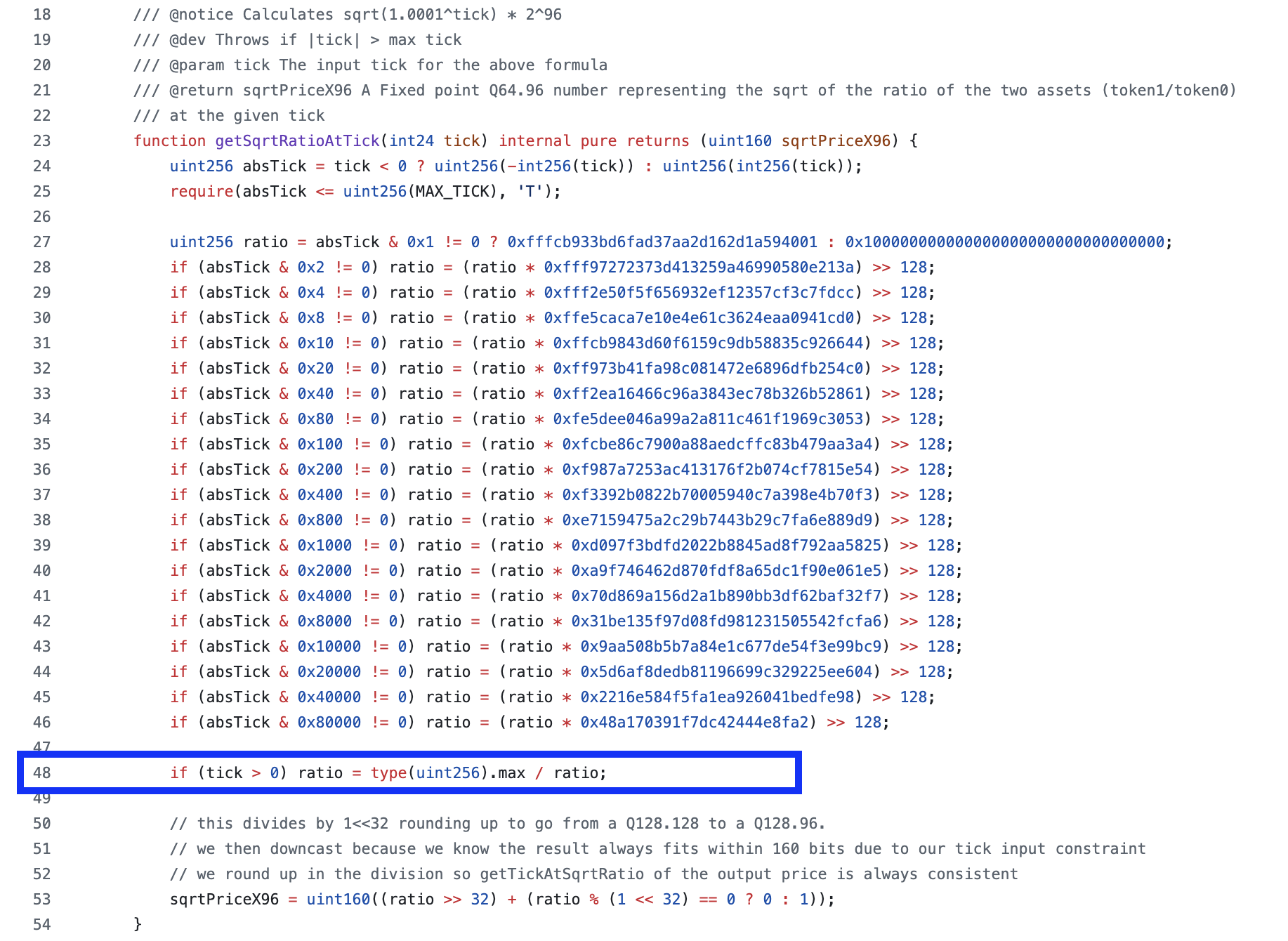
We now explain why the code uses type(uint256).max in the numerator. Note that ratio is the price as a Q128.128 number.
When dividing a fixed-point number by another fixed-point number , we need to multiply the numerator by the scaling factor to prevent the scaling factors from cancelling out.
The value for “1” in Q128.128 is 1 << 128 or . To compute 1 / ratio using Q128.128 we do:
We need to multiply the numerator by the scaling factor, which is . This gives us:
However, the value cannot be encoded in Solidity, the largest value that can be encoded is or type(uint256).max.
This means that the prices computed for positive ticks will be slightly rounded down. The implications of this are discussed at the end.
Part 5/5: converting ratio to sqrtPriceX96 rounding up
The final line of code converts ratio which is a Q128.128 number to a Q64.96 number while rounding up and returns the value.
sqrtPriceX96 = uint160((ratio >> 32) + (ratio % (1 << 32) == 0 ? 0 : 1));
Important details this article did not cover
We made the following observations about the code in this article:
- With the exception for the tick -1, the constants are rounded up
- Computing the reciprocal for positive ticks slightly rounds down because the code approximates as
type(uint256).max. - The final conversion from Q128.128 to Q64.96 rounds up if dividing
ratioby1 << 32isn’t exact (note the ternary operator in the code snippet above that adds 1 ifratiodoesn’t perfectly divide1 << 32).
Empirical test of accuracy
Testing out the Solidity function can be done simply by copying the code into an IDE.
We can create a reference implementation in Python as follows to get the correct value for
as
from decimal import *
getcontext().prec = 1000 # set the precision very high
# 2**96 * (1.0001)^(tick/2)
math.ceil(Decimal(2**96)*(Decimal(10001)/Decimal(10000))**(Decimal(tick)/2))
(Note: one can also use a full precision calculator online).
We can compare the outputs for the extreme ticks:
# tick 887272 (MAX_TICK)
solidity: 1461446703485210103287273052203988822378723970342
python : 1461446703485210103244672773810124308346321380903
# tick 0
solidity: 79228162514264337593543950336
python : 79228162514264337593543950336
# tick -887272 (MIN_TICK)
solidity: 4295128739
python : 4295128739
If we check the MAX_TICK, we see that the Solidity code overestimates the true value:
solidity: 14614467034852101032 87273052203988822378723970342
python : 14614467034852101032 44672773810124308346321380903
Whether this error is serious or not depends on how downstream logic uses this function.
getSqrtRatioAtTick() is used when liquidity providers add or remove liquidity and when traders do a swap that crosses a tick. Since we have not yet discussed either of those mechanisms at this stage in our tutorial of Uniswap V3, we defer an error analysis of this function.
Summary
To compute the square root price at a tick, getSqrtRatioAtTick() first computes the absolute value of the tick (), and then loops over the 20 most significant bits of to compute . If the original tick was positive, it recomputes the price as . Finally, it converts the 128-bit fixed point representation to a 96 bit representation and returns that as the price.