Square Roots of Roots of Unity

The square root of a number $x$ is $y$ such that $y^2=x$. When $x$ is of the form $x^m$ and $m$ is even, then the square root is easy to compute: it’s simply $x^{m/2}$. This follows from the power rule of exponents:

$$ x^\frac{m}{2}\cdot x^\frac{m}{2}=x^{\frac{m}{2}+\frac{m}{2}}=x^\frac{2m}{2}=x^m$$

If we restrict exponents to be integers, then $x^{m}$ has a square root if and only if $m$ is even. Therefore, $x^\frac{m}{2}$ is a square root of $x^m$.

Square roots have two solutions. For example, the integer square root of 4 is 2 and -2. Thus, we also know that if $x^{m/2}$ is a square root of $x^m$, then $-x^{m/2}$ is also a square root. We can verify this algebraically as

$$ (-x^\frac{m}{2})(-x^\frac{m}{2})=(-1)(-1)(x^\frac{m}{2})(x^\frac{m}{2})=x^\frac{m}{2}x^\frac{m}{2}=x^m$$

Examples of computing the square roots of numbers in exponent form

Example 1: What is the square root of $17^{52}$ ?

The exponent is even, so we can divide the exponent by two. The answer is $17^{26}$ and $-17^{26}$.

Example 2: What is the square root of $13^{8k}$?

Because $k$ is multiplied by 8, it doesn’t matter if $k$ is even or not because the product will be even, so we know the exponent can be divided by two. Half of $8k$ is $4k$ so the answer is $13^{4k}$ and $-13^{4k}$

Example 3: What is the square root of $a^{2c}$?

Again, we don’t need to know $a$ or $c$. The exponent is guaranteed to be even due to the multiplication by two. Dividing the exponent by 2, we get $c$, so the square roots are $a^c$ and $-a^c$.

Exponent rule of square roots

The value $a^{m}$ has square roots $a^{m/2}$ and $-a^{m/2}$. The exponent of the square roots will be integers if and only if $m$ is even.

Applying the exponent rule of square roots to roots of unity

As we’ve seen several times already, the roots of unity are written as powers of a primitive root of unity. Here is the multiplicative subgroup of the 8-th roots of unity:

$$ \set{\omega^0\equiv1,\omega^1,\omega^2,\omega^3,\omega^4\equiv-1,\omega^5,\omega^6,\omega^7}$$

Recall the identity that $-\omega^i=\omega^{k/2+i}$.

Since $k=8$ in our example, $k/2=4$ so $\omega$ and $\omega^{5}$ are $k/2$ apart. Thus, we can also write the 8-th roots of unity as

$$ \set{1,\omega,\omega^2,\omega^3,-1,-\omega,-\omega^2,-\omega^3}$$

Based on the exponent rule of square roots, only the even powers of omega have square roots (we consider 0 to be even in this context):

$$ \set{\boxed{\omega^0\equiv1},\omega^1,\boxed{\omega^2},\omega^3,\boxed{\omega^4\equiv-1},\omega^5,\boxed{\omega^6},\omega^7}$$

We can compute their square roots as follows:

  • $\sqrt{\omega^0}=1, -1$ or equivalently $\omega^0$ and $\omega^4$
  • $\sqrt{\omega^2}=\omega,-\omega$ or equivalently $\omega$ and $\omega^5$
  • $\sqrt{\omega^4}=\omega^2,-\omega^2$ or equivalently $\omega^2$ and $\omega^6$
  • $\sqrt{\omega^6}=\omega^3,-\omega^3$ or equivalently $\omega^3$ and $\omega^7$

If we visualize the 8-th roots of unity on the circle, we note that only the members of the red subgroups (the even powers, or equivalently the powers of $\omega^2$) have square roots:

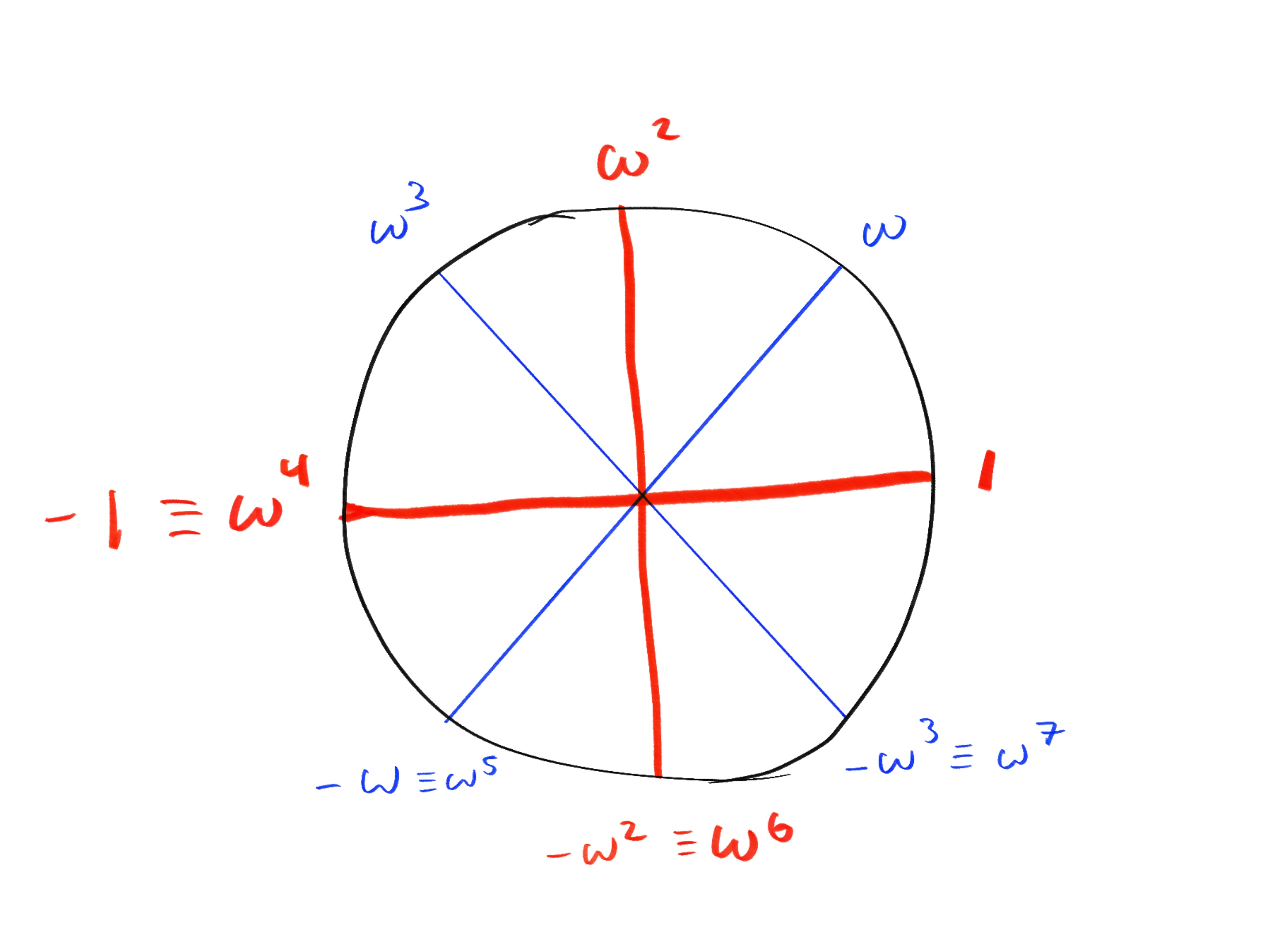
A diagram showing that the square roots of the 4-th roots of unity are the 8-th roots of unity.

The following diagram shows how each square root evaluation results in two opposite points on the circle:

A diagram showing square roots on the unit circle for 1, -1, omega^2 and omega^6

Taking the square root of the k-th roots of unity produces the 2k-th roots of unity (if they exist)

In a previous chapter, we saw that squaring the roots of unity halves the size of the set (assuming the set is even in size). Taking the square root of the roots of unity doubles the size of the set. For example, consider the 8-th roots of unity generated by $\omega$ as shown above:

$$ \set{1,\omega,\omega^2,\omega^3,\omega^4,\omega^5,\omega^6,\omega^7}$$

If we square each element, we get the set:

$$ \set{1,\omega^2,\omega^4,\omega^6}$$

Now, if we take the square root of each element in this new set, we get the original 8-th roots of unity as shown in the section above:

  • $\sqrt{\omega^0}=1, -1$ or equivalently $\omega^0$ and $\omega^4$
  • $\sqrt{\omega^2}=\omega,-\omega$ or equivalently $\omega$ and $\omega^5$
  • $\sqrt{\omega^4}=\omega^2,-\omega^2$ or equivalently $\omega^2$ and $\omega^6$
  • $\sqrt{\omega^6}=\omega^3,-\omega^3$ or equivalently $\omega^3$ and $\omega^7$

This is not a profound observation: the square and square roots are opposite operations so naturally the square root should “undo” what the square does and vice versa.

However, this does open up an optimization that we will later leverage. One can square the roots of unity repeatedly to shrink the set down, carry out some operation, then use the square root to “raise” the result back up to the original set. We will introduce the mechanics in the upcoming chapters, but for now, the reader must have the following concept absolutely mastered:

Squaring $k$-th roots of unity reduces the set to the $k/2$-th roots of unity. Taking the square roots of the $k/2$-th roots of unity produces the $k$-th roots of unity and doubles the set size.

Summary

  • Only even powers of the roots of unity have square roots
  • The square roots of $\omega^m$ are $\omega^{m/2}$ and $-\omega^{m/2}$
  • Based on an earlier chapter, we know $-\omega^{m/2}\equiv\omega^{m/2+k/2}$
  • Visualizing square roots on a circle. Since square roots are always additive inverses of each other, the square root of a root of unity is on “opposite sides” of the circle.

Practice Problems

  1. Let $\omega$ be the primitive 4-th root of unity. What are the square roots of $-\omega^2$?
  2. Let $\omega$ be the primitive 32-th root of unity. What are the square roots of $-\omega^{16}$?
  3. Let $\omega$ be the primitive 16-th root of unity. What are the square roots of $-1$?