Storage Slots of Dynamic Types (Mappings, Arrays, Strings, Bytes)

Dynamic-sized types in Solidity (sometimes referred to as complex types) are data types with variable size. They include mappings, nested mappings, arrays, nested arrays, strings, bytes, and structs that contain any of those types. This article shows how they are encoded and kept in storage.

Mappings

Mappings are used to store data in the form of key-value pairs.

The colored key values below will be referred to in an upcoming code block:

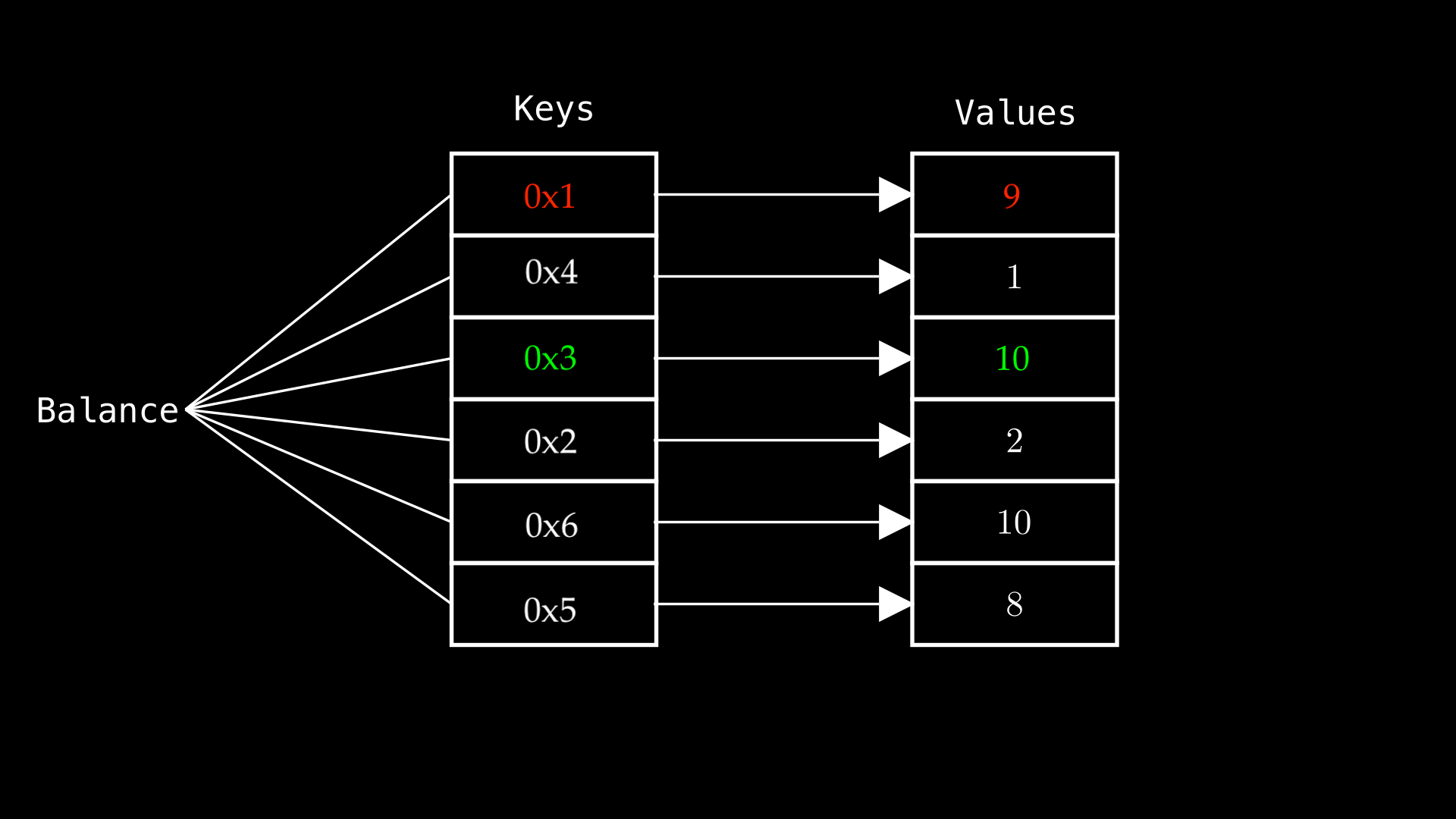
Consider this example that uses mappings to associate an Ethereum address with a value. The red and green key values, as shown in the diagram above, are set in the code below:

// SPDX-License-Identifier: MIT
pragma solidity =0.8.26;

contract MyMapping {
    mapping(address => uint256) private balance; // storage slot 0

    function setValues() public {
        balance[address(0x01)] = 9;      // RED
        balance[address(0x03)] = 10;     // GREEN
    }
}

The function setValues maps the addresses 0x01 and 0x03 to 9 and 10 respectively, storing them in the mapping variable balance. To get the value assigned to address(0x01) using Solidity is straightforward. But what storage slot is it using, and how do we access it with assembly?

Storage Slot For Mappings

To compute the storage slot of the value, we take the followings steps:

1. Concatenate the key associated with the value and the mapping variable storage slot (base slot)
2. Hash the concatenated result.

Formula for the above steps

$\texttt{byte32} \,\,\,\text{storageSlot}\,=\texttt{keccak256}(\texttt{byte32}(\text{key}) \, \oplus \texttt{byte32}(\text{baseSlot}));$

where $\oplus$ means concatenate

The following animation shows how the data in the formula above is laid out:

Under the hood, the key and base slot are both stored as 256 bit (32 bytes) values. When they are concatenated together, they are a 64 bytes value.

Below is an animation that shows how these values (key and base slot) are concatenated. The values used are:

• address key = 0x504DbB5Dc821445b142312b74693d778a1B60b2f
• uint256 baseSlot = 6

Notice how the key and base slot values were first padded with zeros to 32-byte values before being concatenated together. The result from the concatenation (64 bytes array) are what get hashed to determine the storage slot.

Compute Mapping Storage Slot

Now that we have an idea of how key and base slot are computed to get the storage slot for a mapping, we are ready to see how it’s done manually in Solidity.

Remember, we need two values to calculate the slot for a mapping (key and base slot). The code to accomplish this is in the getStorageSlot() function:

contract MyMapping {
    mapping(address => uint256) private balance; // storage slot 0

    function setValues() public {
        balance[address(0x01)] = 9;      // RED
        balance[address(0x03)] = 10;     // GREEN
    }

    //*** NEWLY ADDED FUNCTION ***//
    function getStorageSlot(address _key) public pure returns (bytes32 slot) {
            uint256 balanceMappingSlot;

            assembly {
                 // `.slot` returns the state variable (balance) location within the storage slots.
                 // In our case, balance.slot = 0
                 balanceMappingSlot := balance.slot
            }

            slot = keccak256(abi.encode(_key, balanceMappingSlot));
        }
}

The getStorageSlot function takes in _key as argument and uses an assembly block to get the base slot (balanceMappingSlot) for balance variable. It then uses abi.encode to pad each value to 32 bytes and concatenate them, then hashes the concatenated value using keccak256 to produce the storage slot.

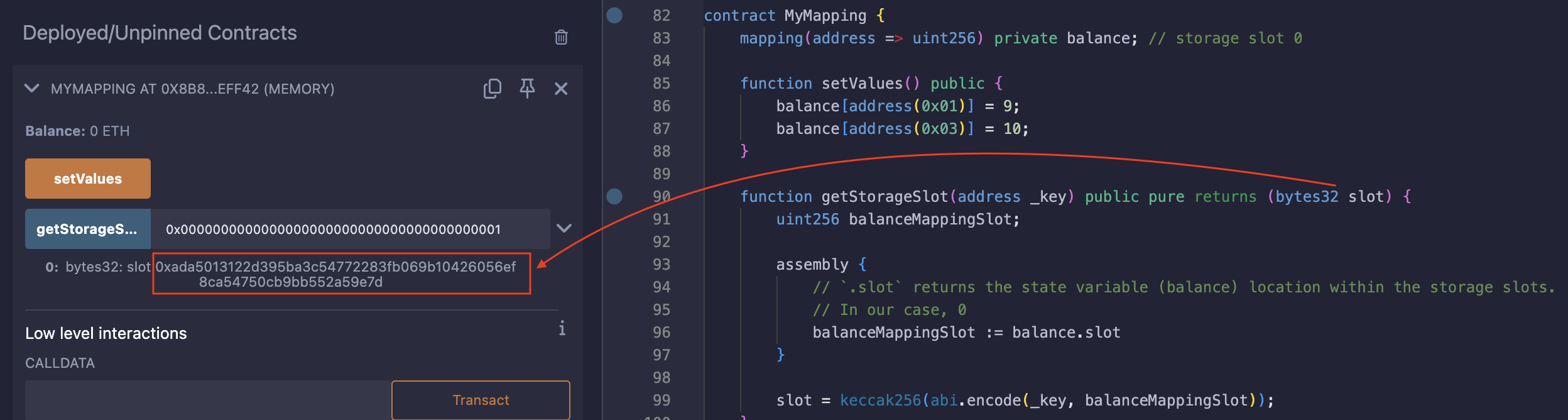
To test this, let’s call the function with address(0x01) as the argument, since we have already assigned a value to the storage slot associated with this _key in the setValues function.

The slot returned after the call: 0xada5013122d395ba3c54772283fb069b10426056ef8ca54750cb9bb552a59e7d

Next, we create a getValue() function which will load the storage slot we calculated. This function is to prove that the slot computed by getStorageSlot() is indeed the correct storage slot that holds that value.

function getValue(address _key) public view returns (uint256 value) {
    // CALL HELPER FUNCTION TO GET SLOT 
    bytes32 slot = getStorageSlot(_key);

    assembly {
        // Loads the value stored in the slot
        value := sload(slot)
    }
}

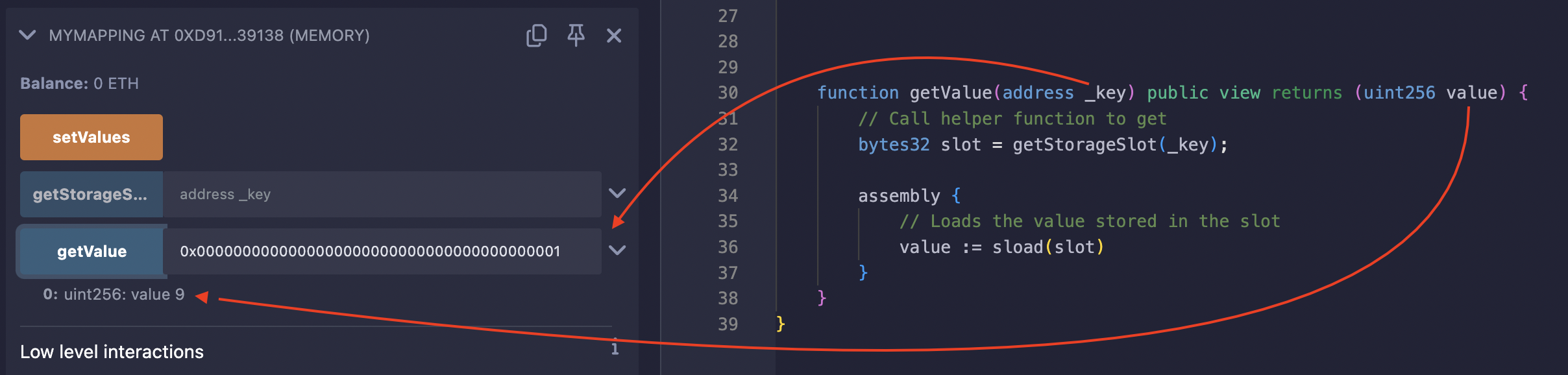
Calling the getValue function with address(1) as argument returned 9, which is the correct value assigned to the address(1) key:

Here’s the complete code for you to test on Remix.

// SPDX-License-Identifier: MIT
pragma solidity =0.8.26; 

contract MyMapping {
    mapping(address => uint256) private balance; // storage slot 0

    function setValues() public {
        balance[address(0x01)] = 9;
        balance[address(0x03)] = 10;
    }

    function getStorageSlot(address _key) public pure returns (bytes32 slot) {
        uint256 balanceMappingSlot;

        assembly {
            // `.slot` returns the state variable (balance) location within the storage slots.
            // In our case, 0
            balanceMappingSlot := balance.slot
        }

        slot = keccak256(abi.encode(_key, balanceMappingSlot));
    }

    function getValue(address _key) public view returns (uint256 value) {
        // Call helper function to get 
        bytes32 slot = getStorageSlot(_key);

        assembly {
            // Loads the value stored in the slot
            value := sload(slot)
        }
    }
}

Nested Mappings

A nested mapping is a mapping within another mapping. A common use case for this is storing the balances of different tokens for a specific address, as shown in the diagram below.

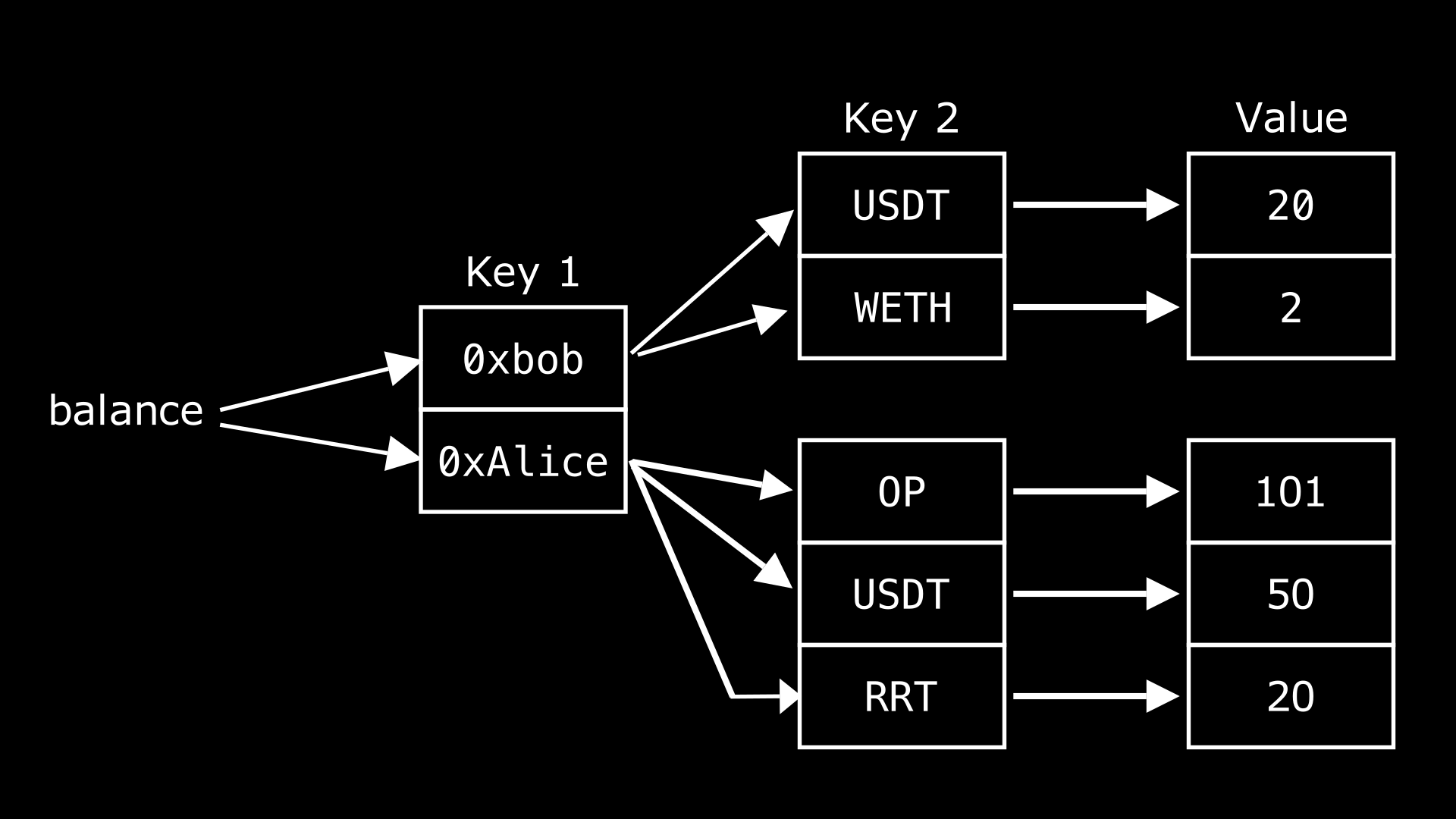
This shows that the balance variable holds two different addresses, 0xbob and 0xAlice, each of these addresses is associated with multiple tokens, which in turn map to different balances, hence, nested mappings.

Storage Slot For Nested Mappings

The calculation of storage slots for nested mappings is similar to that of single mappings, with the difference being that the “level” of mapping corresponds to the number of hash operations. Below is an animation and a code example that demonstrates a two-level mappings with two hash operations:

Now let’s show a code example of getting nested array value from storage using assembly

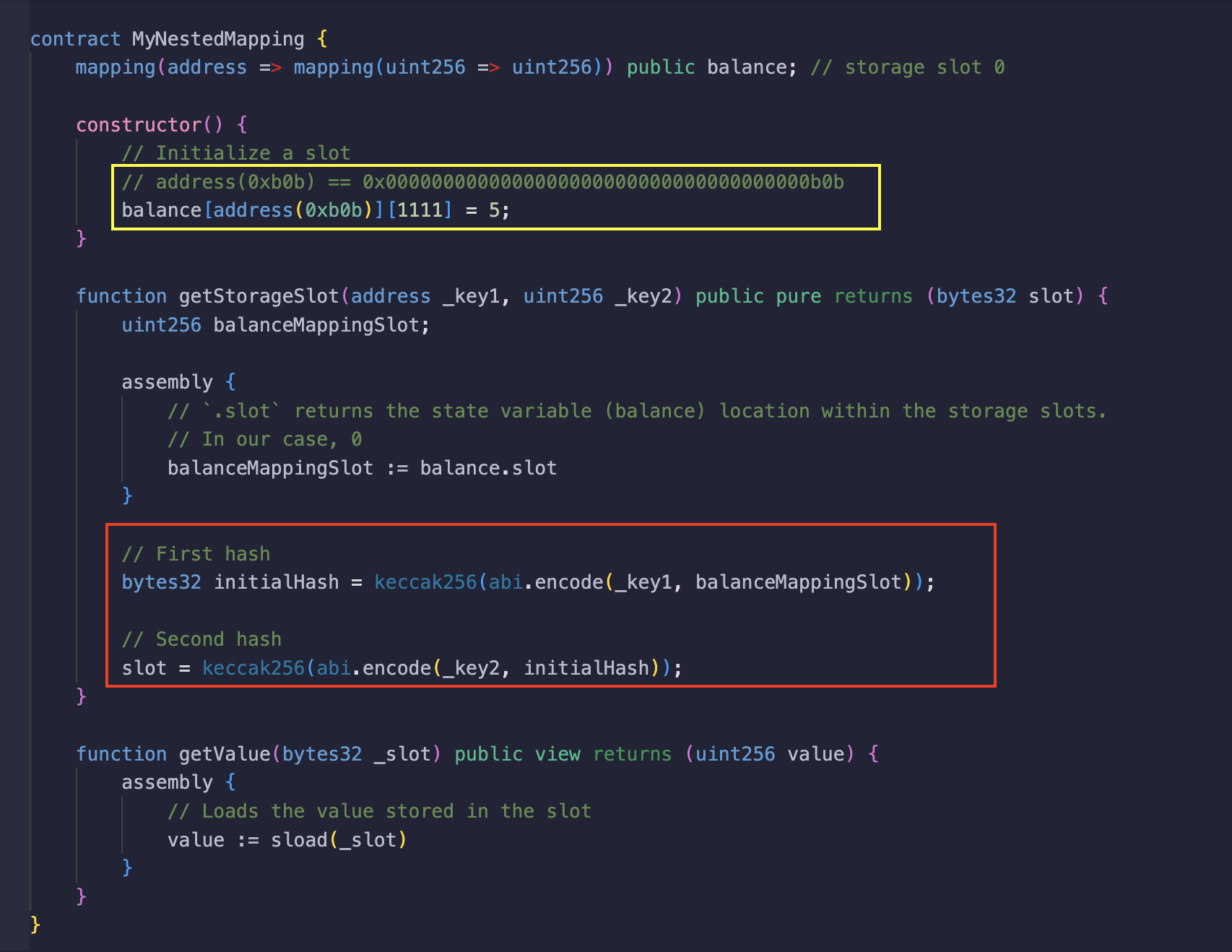
In the screenshot below, the value 5 is assigned to the balance mapping with the keys, address(0xb0b) (owner) and 1111 (tokenID), as highlighted in the yellow box. The contract has two functions;

• The getStorageSlot function which takes in two arguments which are the keys needed to derive the desired slot. There are also two hash operations happening in the function, as seen in the red box:
  • the first is the hash of the _key1 (owner) and the balance mapping slot, which is then stored in initialHash variable.
  • the second is the hash of _key2 (tokenID) and initialHash, to get the slot of balance[_key1][_key2]. If it were a 3-level mappings, the third key (_key3) would be hashed with the value from the second hash operation to get the desired storage slot and so on.
• The getValue function which takes in a slot as argument and returns the value held in it, which behaves the same as the previous example.

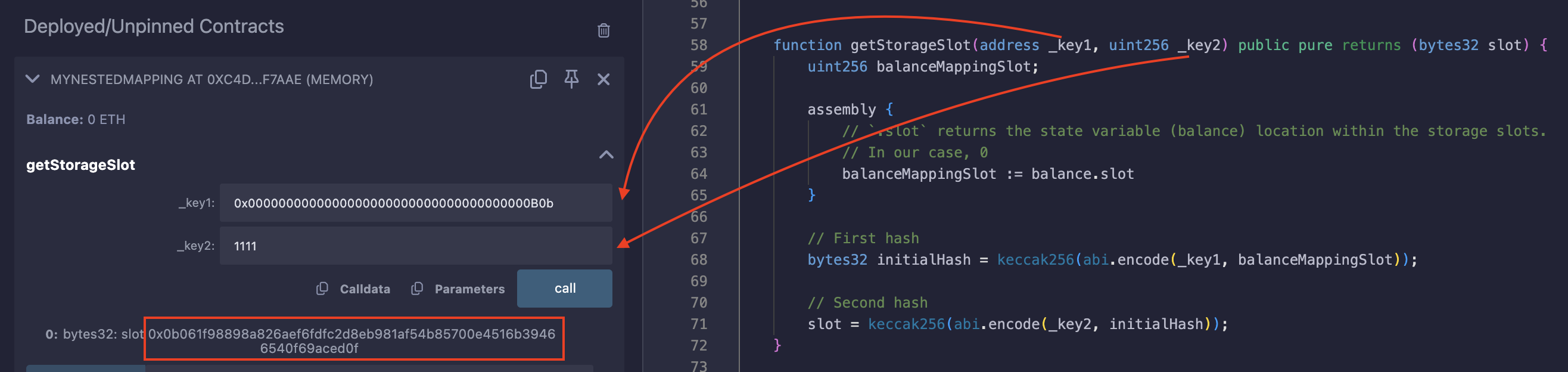
Calling the getStorageSlot function with the following arguments, address(0xb0b) and 1111, returns the following slot:

0x0b061f98898a826aef6fdfc2d8eb981af54b85700e4516b39466540f69aced0f

To show that the calculated slot holds the value 5, we will call the getValue function and pass the slot as argument. This function uses the sload opcode to load the slot and then return its value:

And yes! We got the same value 5 that we inserted in the constructor.

Array

This is a dynamic type in Solidity used to store an indexed collection of elements of the same type, either primitive or dynamic. Solidity supports two array types: fixed-size and dynamic, with different storage allocation methods.

Fixed-Size Arrays

This type of array has a predetermined size that cannot be changed after the array is declared.

Slot Allocation For Fixed-size Array

If the type of each array element occupies a storage slot capacity (256 bits, 32 bytes, or 1 word), the Solidity compiler treats these elements as individual storage variables, assigning them slots sequentially starting from the slot of the array’s storage variable.

Consider the contract below:

contract MyFixedUint256Array {
    uint256 public num; // storage slot 0

    uint256[3] public myArr = [
                                4, // storage slot 1 
                                9, // storage slot 2
                                2  // storage slot 3
                            ]; 
}

Since num is of type uint256 and is the first state variable in the contract, it occupies the whole of storage slot 0. The second state variable, myArr, is a fixed-size array of uint256 with three elements, meaning each element will occupy its own storage slot, starting from slot 1.

The animation below shows how storage slots are allocated to each variable, detailing how the values in each storage variable are stored in slots.

Let’s look at another example, similar to the previous one, but this time using uint32 as the data type for the array:

contract MyFixedUint32Array {
    uint256 public num; // storage slot 0

    uint32[3] public myArr = [
                                4, // storage slot ??? 
                                9, // storage slot ???
                                2  // storage slot ???
                            ]; 
}

Before reading further, can you tell the storage slot for the third element in the array? If you’re thinking it might be slot 3, similar to the previous example, you might want to reconsider.

If the type of each array element doesn’t occupy an entire storage slot, like the uint32 in this example, the compiler packs multiple elements together within a single slot until it is filled or there isn’t enough space for the next element before moving to the next slot. This is similar to how storage variables are packed together by the compiler when they don’t individually occupy a full slot.

How packed values are allocated slot:

Note: Accessing a packed element will incur more gas since the EVM needs to add additional instructions other than the usual sload. It is only advisable to pack your elements if they are typically accessed in the same transaction and thus can share cold load costs.

Dynamic Arrays

Unlike fixed-size array that has its size predetermined at compile time, dynamic array can change size at runtime.

Slot Allocation For Dynamic Array

Generally, dynamic arrays have their length stored somewhere since it is not known at compile time. Solidity follows this principle by storing the length of a dynamic array in a separate storage slot. Below is how slots are allocated to both the length and the element(s) of a dynamic array.

The storage slot allocated for the length of the array is the same slot for the array storage variable (base slot). Below is an example that illustrates this:

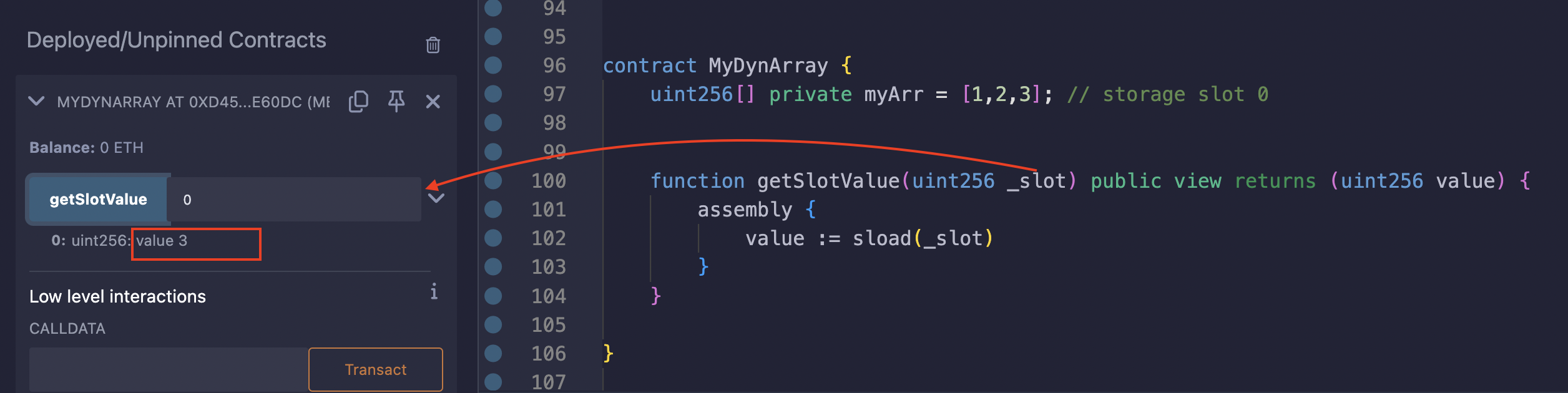
The myArr variable has three elements, giving it a length of 3. The getSlotValue function, as its name suggests, takes a slot number and returns the value stored in it. In our case, we passed slot 0 as the argument because that is the slot allocated for the myArr storage variable. We then used the sload opcode to load the value from the slot.

Array values are kept in storage slots sequentially, with each storage slot being an index in the array. The storage slot for the first element (index 0) is determined by the keccak256 hash of the base storage slot (the slot where the variable is declared). The image below illustrates this.

The keccak hash of the slot 2 points to the slot holding the first element, then we keep adding 1 to that value to get the storage locations of other indexes in the array:

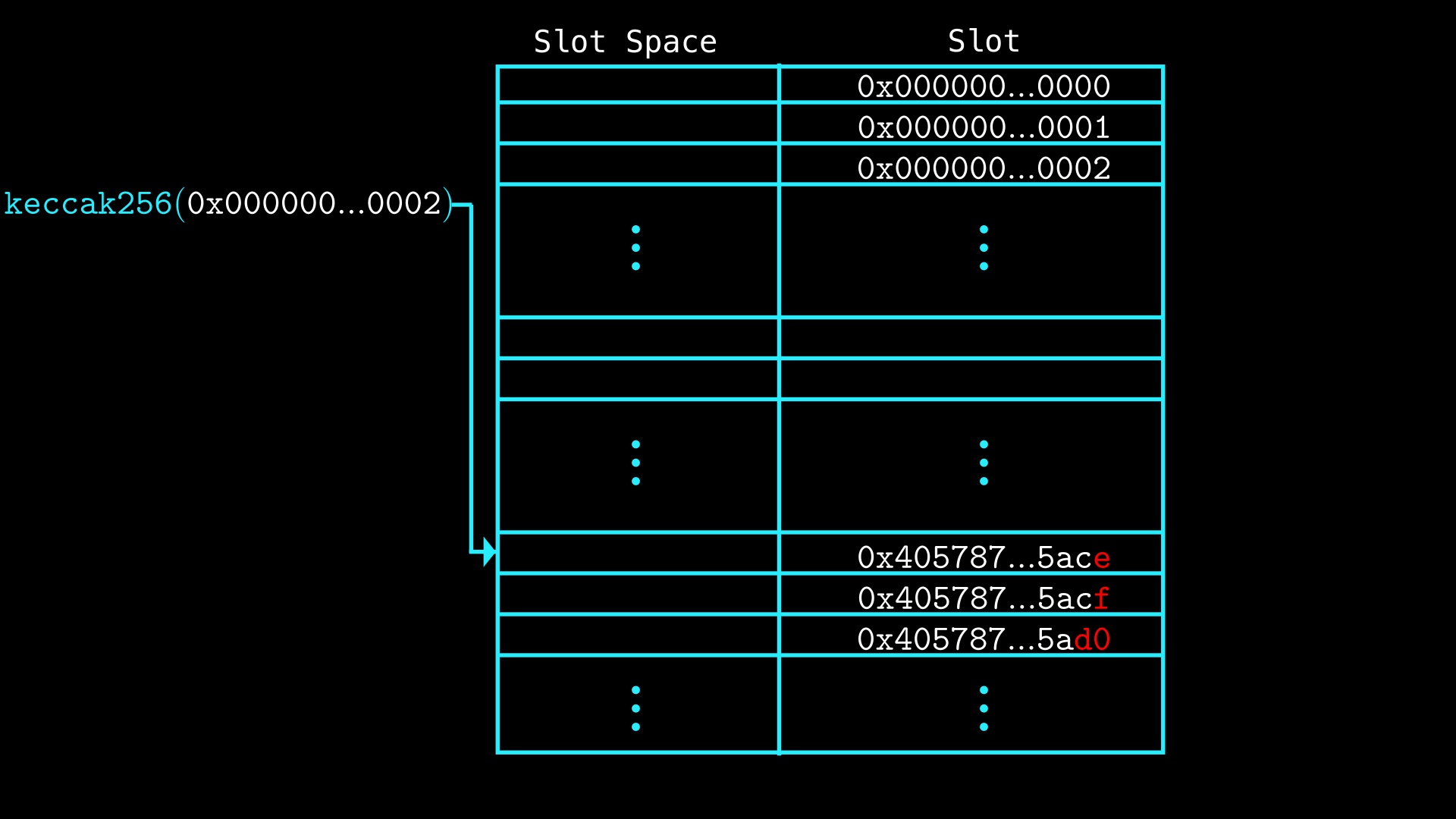
Storage slots are numbered from 0 to 2²⁵⁶ – 1, and that is exactly the range of values a keccak256 outputs. The first red value in the image (0x405787...5ace) represents the hashed storage location derived from slot 2, which holds the first element of the array. Each subsequent value (0x405787...5acf, 0x405787...5ad0) is an increment of the previous one, corresponding to the next element in the array. This pattern continues for each additional element, with the storage location incrementing sequentially based on the array’s size.

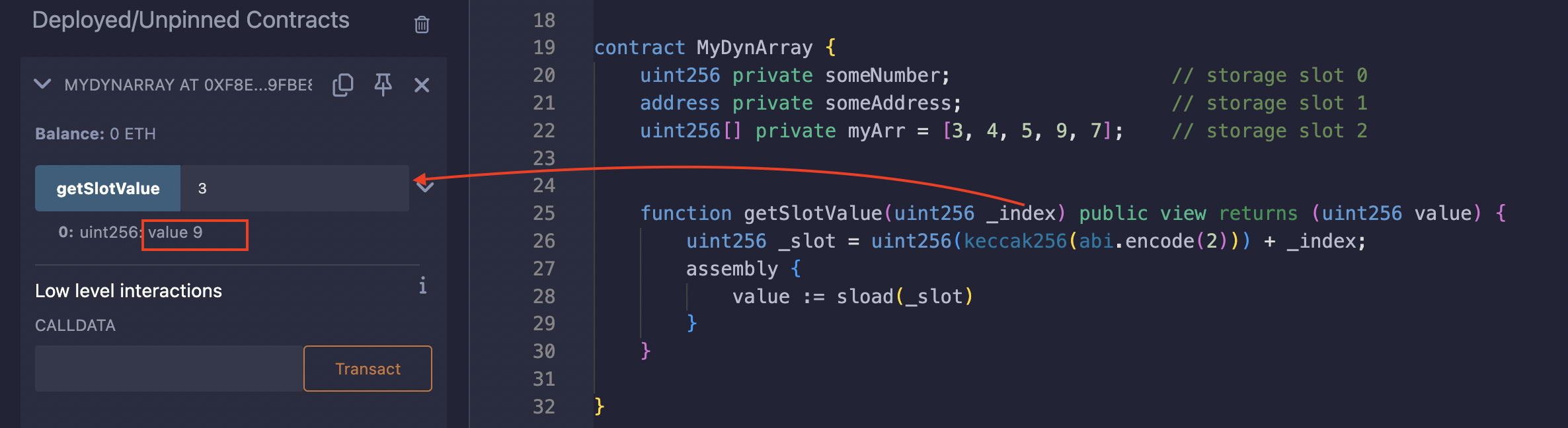
For example, consider an array of length 5 located at storage slot 2, containing the elements [3, 4, 5, 9, 7] of type uint256:

contract MyDynArray {
    uint256 private someNumber;                   // storage slot 0
    address private someAddress;                  // storage slot 1
    uint256[] private myArr = [3, 4, 5, 9, 7];    // storage slot 2

    function getSlotValue(uint256 _index) public view returns (uint256 value) {
        uint256 _slot = uint256(keccak256(abi.encode(2))) + _index;
        assembly {
            value := sload(_slot)
        }
    }

}

To find the storage slot that holds the value 9, we first hash the base slot (2) using keccak256. We then add the index of the element (index = 3) to the hashed value. This calculation gives us the specific storage slot holding the value 9. Lastly, we sload the value in the gotten _slot.

Test on remix:

What happens when elements don’t use up a storage slot space?

Elements are packed into storage slots until the available space is filled. Only types like 128 bits (16 bytes ) or smaller can be packed. However, addresses, which take 20 bytes each, are not packed since two addresses (40 bytes) is more than the size of a single storage slot.

Let’s change myArr to use uint32 instead of uint256 in MyDynArray contract:

contract MyDynArray {
    uint256 private someNumber;                   // storage slot 0
    address private someAddress;                  // storage slot 1
    uint32[] private myArr = [3, 4, 5, 9, 7];     // storage slot 2

    function getSlotValue(uint256 _index) public view returns (bytes32 value) {
        uint256 _slot = uint256(keccak256(abi.encode(2))) + _index;
        assembly {
            value := sload(_slot)
        }
    }

}

The following changes has been made:

• uint256[] ⇒ uint32[]: the data type for the dynamic array.
• uint256 value ⇒ bytes32 value: the return value, so we can easily see how the values are packed.

Each element occupies 4 bytes out of the available 32 bytes per storage slot. With 5 elements, the total size is 4 * 5 = 20 bytes. This means all the elements can fit within a single storage slot, with some space remaining.

Test on remix:

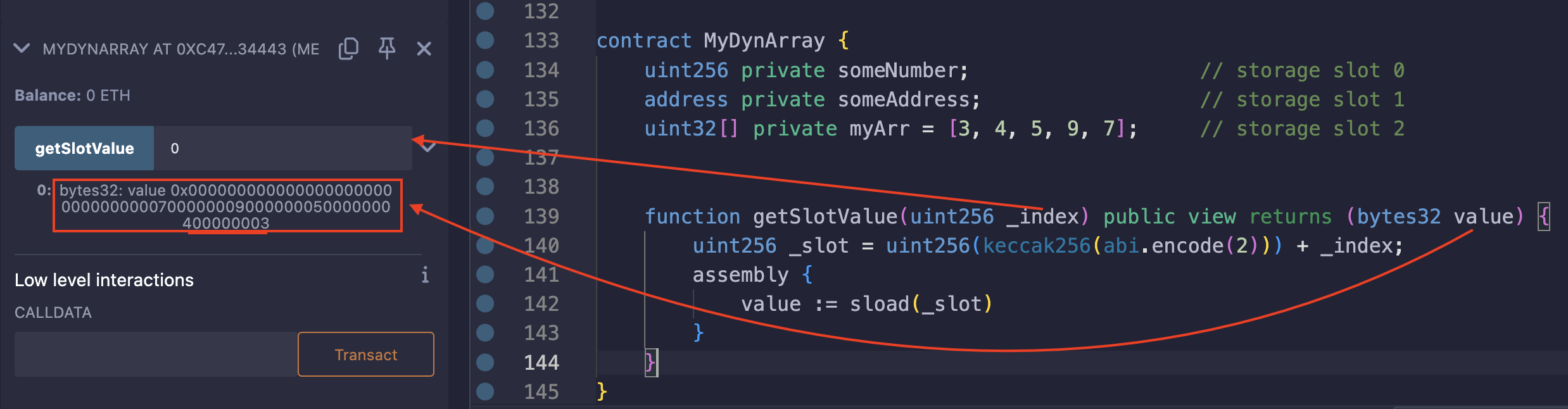
The return value:

Nested Array

A nested array is an array that holds other arrays. It can be used to represent matrix-like data, where the elements within each row is an array, and the column is an index within that array.

The explanation animation below uses C to refer to columns and R to refer to rows.

C ⇒ green

R ⇒ red

Storage Slot For Fixed-Size Nested Array

The compiler allocates slots for elements in a fixed-size nested array just like it does for a regular fixed-size array. Each element is allocated a slot incrementally, starting from the base slot, if it occupies an entire slot. Otherwise, it is packed together with other elements until the slot space is filled up.

Here’s a simple animation that illustrates how a fixed-size nested array stores data:

Storage Slot For Dynamic Nested Array

As we already know, the steps to determine the storage slot for a specific element in a dynamic array are as follows:

1. keccak hashing the base slot
2. then adding the element’s index to the hash value

For dynamic nested arrays, the process involves repeating the above steps for each level of nesting to find the final slot.

Let’s say we have a two-levels nested array, that is, array(s) within an array:

$\texttt{uint256[][]}\,\,\text{array}\,=\,[\,[a,\,b,\,c],\,[d,\,e,\,f]\,]$

The steps to determine the storage slot for element f are:

1. keccak hashing the array base slot then adding the index of the sub-array that holds the element. In our case, the second sub-array.
2. keccak hashing the result from step1 then adding the index of element f in the sub-array.

Here’s an animation that illustrates the above steps:

We first hash the base slot and add the index of the sub-array (sub-array1, which is index 1 in the base array), which gives us the initial hash (the slot holding the sub-array). Next, we hash this initial hash and add the index of element f (which is 2) within sub-array1 to determine the final slot.

A practical example of getting the slot for an element in a uint256 dynamic nested array:

contract MyNestedArray { 
    uint256 private someNumber;                     // storage slot 0

        // Initialize nested array
    uint256[][] private a = [[2,9,6,3],[7,4,8,10]]; // storage slot 1


    function getSlot(uint256 baseSlot, uint256 _index1, uint256 _index2) public pure returns (bytes32 _finalSlot) {
                // keccak256(baseSlot) + _index1
        uint256 _initialSlot = uint256(keccak256(abi.encode(baseSlot))) + _index1;

                // keccak256(_initialSlot) + _index2
        _finalSlot = bytes32(uint256(keccak256(abi.encode(_initialSlot))) + _index2);
    }

    function getSlotValue(uint256 _slot) public view returns (uint256 value) {
        assembly {
            value := sload(_slot)
        }
    }
}

Suppose we want to find the storage slot that holds the element 8 in the array [[2,9,6,3],[7,4,8,10]] in the contract above.

1. We need to identify three things:

   1. the base slot of the nested array
   2. the index of the sub-array containing the element,
   3. and the index of the element within that sub-array.

   These indexes are needed to get our desired slot.

2. We call the getSlot function passing the values for the baseSlot and indexes:

   1. baseSlot: the slot for array a, which is slot 1.
   2. _index1: the sub-array ([7,4,8,10]) containing the element is at index 1.
   3. _index2: the element 8 within the sub-array is at index 2.

   The returned slot after the call:

   0xea7809e925a8989e20c901c4c1da82f0ba29b26797760d445a0ce4cf3c6fbd33

3. Lastly, call the getSlotValue function passing the returned slot from step2.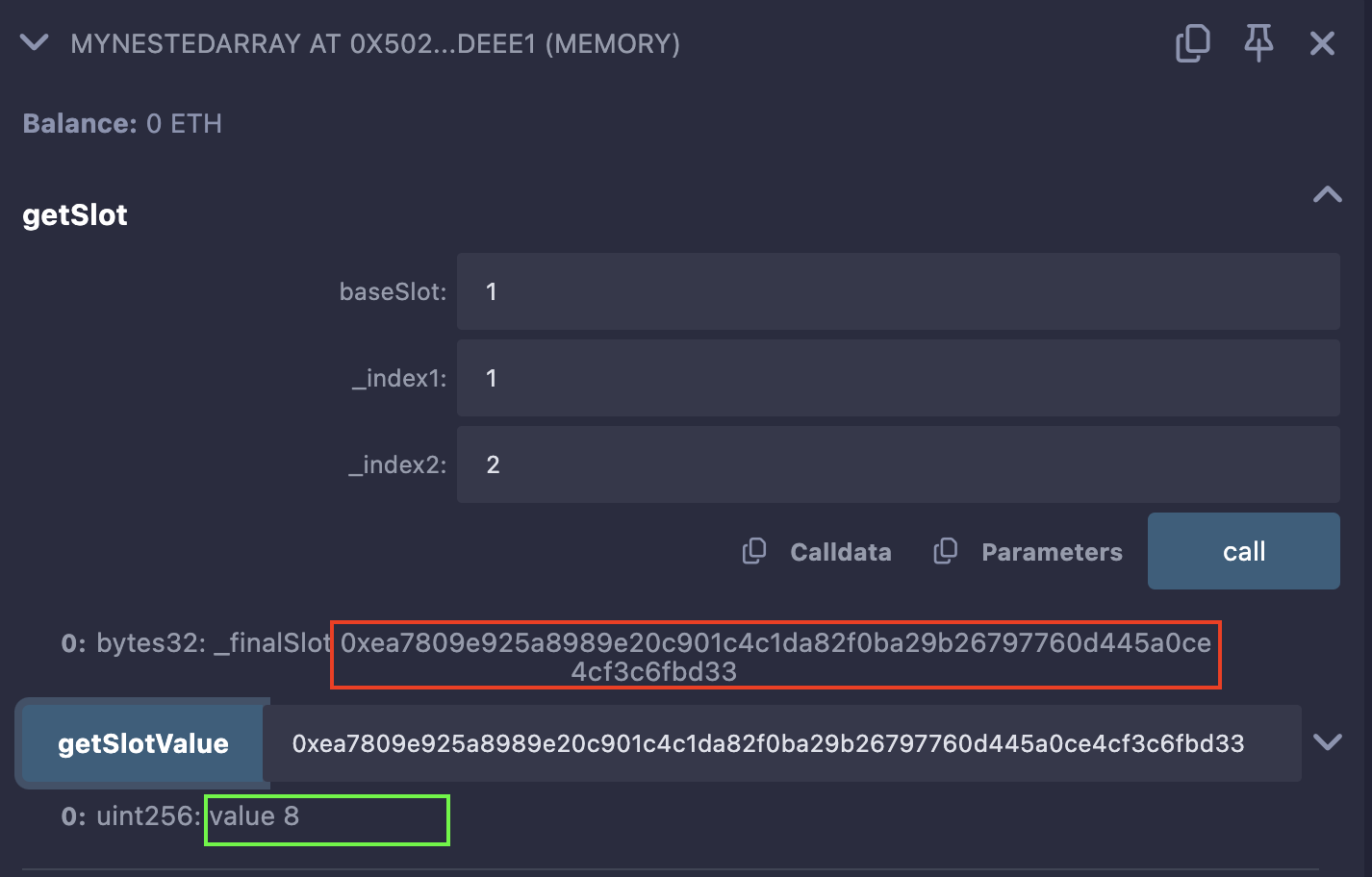

   

String

Strings in Solidity are dynamic types, meaning they don’t have a fixed length. Some strings may fit within a single storage slot, while others may require multiple slots.

Consider the following example contract:

contract String {
    string public myString;
    uint256 public num; 
}

The storage slot of the string is 0 and the storage slot of the uint256 is 1.

If we store a short string data in myString (one that is less than 32 bytes, we will discuss why 32 bytes string is also considered a long string later), we can retrieve it from slot 0 without any issues.

However, if we store a longer string data, let’s say one that takes up 42 bytes, it would overflow slot 0 and overwrite slot 1, which is reserved for the num variable initially.

This happens because slot 0 isn’t large enough to contain the longer string. To prevent this issue, Solidity uses different methods for allocating storage slots for string types, depending on the string’s length.

Storage Slot For Strings

The storage variable slot (base slot) stores the string together with information about its length for short strings or only information about its length for long strings, and these cases will be studied in different sections below.

Short String (≤ 31 bytes):

The string data and its length are stored together in the base slot. The string is packed from the left, with its length stored in the rightmost byte of the slot. For short strings, the maximum length of the string is 31 characters. However, what actually gets stored by the protocol is the length of the string multiplied by 2, since each character occupies one byte in storage. This means that the maximum value that can be stored for a short string is 31 * 2 = 62, which is 0x3e in hexadecimal.

Below is an example of a short string Hello World in hex. The zeros are free space that can be used to store a longer string of up to 31 bytes, and the last byte holds the (length of the string) * 2.

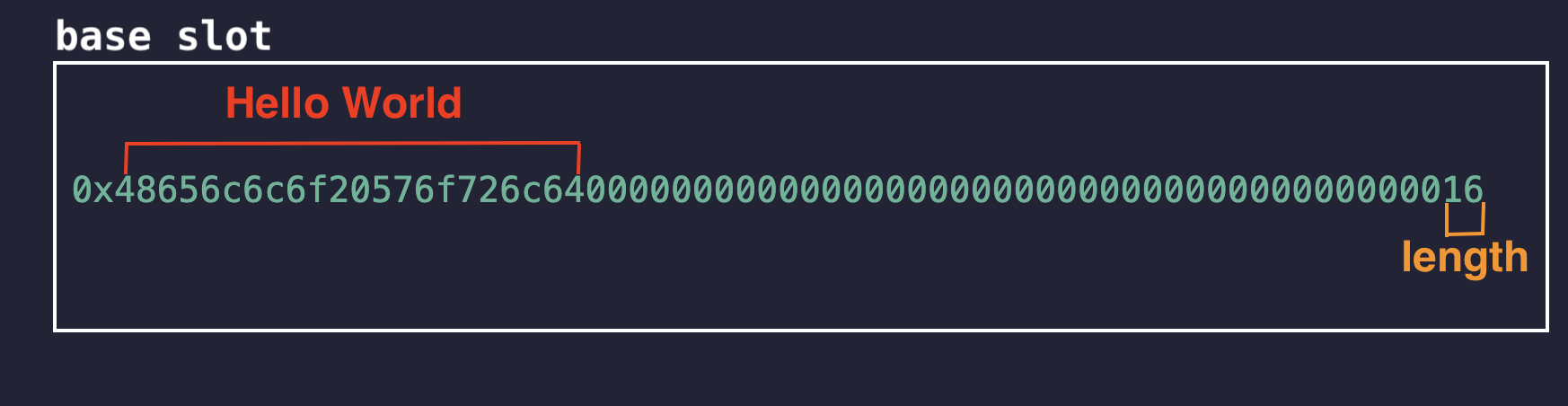
Here 0x16 = 22 is 2 * 11, where 11 is the length of the string Hello World

Long String (> 31 bytes):

The (length of the string * 2) + 1 (we will explain the reason for adding 1 shortly) is stored in the base slot, then the string in hex is stored in a continuous storage slot space. The first 32 bytes of the string data are stored at the keccak256 hash of the base slot. The next 32 bytes are stored at the hash of the base slot plus one, and the next, hash plus two, and so on, until the entire string is stored.

The following animation shows how the length and long string (in hex) are stored in storage slots:

Before the length of a long string is stored, the compiler adds one to it (making it go from even to odd). For example, the string in the animation above takes up 47 bytes (32 + 15), meaning its length is 47 * 2 = 94 (0x5e in hex). Solidity compiler then adds 1 to this length, making it 95 (0x5f in hex), and stores this value in the base slot.

The reason for this is to allow the runtime bytecode to efficiently differentiate between short and long strings. For short strings, the length is always even, so the last bit of the value stored in the base slot will always be zero. On the other hand, long strings (32 bytes or longer) always have an odd length, meaning the last bit will always be one.

Optimized Even And Odd Check

The common method in most programming languages to check if a number is even or odd is by using the modulus operator (num % 2) and checking if the remainder is 0. This also applies in Solidity. However, a more optimized way is to use the bitwise AND operation: num & 1 == 0. Below is an example of both methods and their respective costs:

contract ModMethod {
        // Gas cost: 761 
    function isEven(uint256 num) public pure returns (bool x) {
        x = (num % 2) == 0;
    }
}

contract BitwiseAndMethod {
        // Gas cost: 589
    function isEven(uint256 num) public pure returns (bool x) {
        x = (num & 1) == 0;
    }
}

Get Length Of String

String type in Solidity does not have length property. This is because some characters, particularly those in non-ascii, can take up more than one byte, so tracking how many characters there are when they could have different size creates too much overhead. However, we can see how many bytes the string takes up by casting it to bytes as the example below shows:

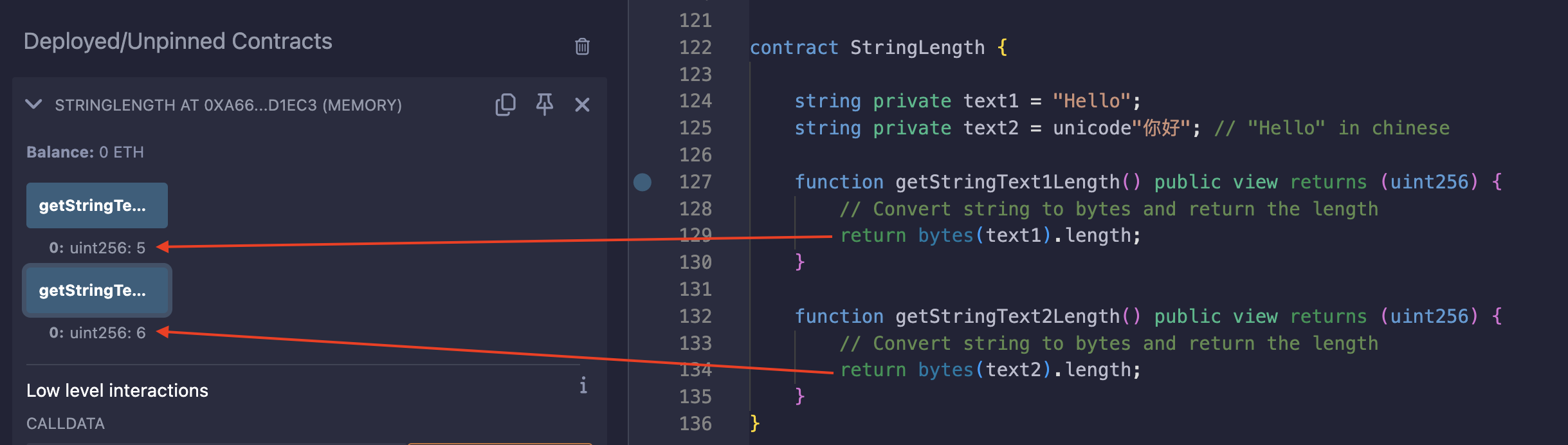
In text2, each character takes 3 bytes, making 6 bytes. To use the length property on a string, you need to convert the string to bytes like in the screenshot.

Bytes

Just like strings, bytes is a dynamic type in Solidity and follows the same set of rules for slot allocation.

• Short ****bytes (≤ 31 bytes): Stored entirely in the base slot, including its length (number of bytes * 2).
• Long ****bytes (> 31 bytes): The base slot stores the length ((number of bytes * 2) + 1), and the actual data is stored in consecutive slots starting from the keccak256 hash of the base slot.

Fixed-Size Bytes

They are types used to store a fixed number of bytes. These types range from bytes1 to bytes32, meaning you can have fixed-size byte arrays that hold between 1 and 32 bytes.

Storing a value that is more or less than the bytes size used will throw a compile time error. In the image below, the variables value2 and value4 are assigned values that are not their expected byte sizes, resulting in a compilation error.

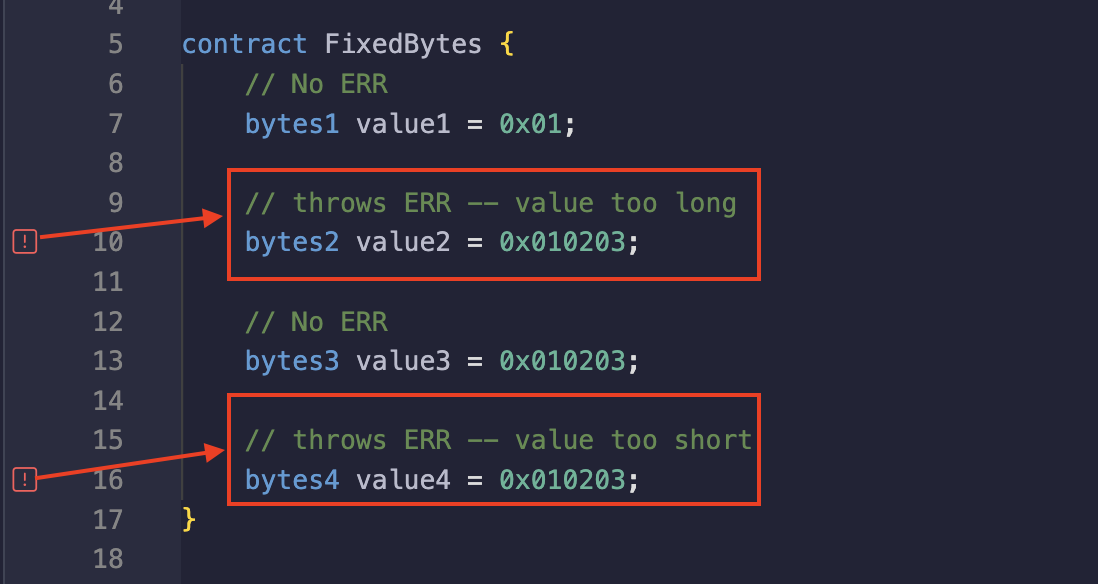
We have used bytes32 in most of our previous code examples to hold keccak256 hashes.

Accessing Individual Byte

A byte within a fixed-size bytes array can be accessed using its index.

For example, the following contract accesses the first byte:

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.9;

contract FixedBytes {
    bytes4 value = hex"01020304";

    function accessFirstByte() public view returns (bytes1) {
            bytes1 individualByte = value[0];  // Access the first byte

        return individualByte;    // Returns the first byte
    }
}

The accessFirstByte function returns a single byte (bytes1). Inside the function, value[0] accesses the first byte of the value array. This byte is then returned.

Prior to Solidity version 0.8.0, the byte type was used instead of bytes1 to represent a single byte. In version 0.8.0 and above, bytes1 is now the preferred type to hold single byte values.

Comparison of string/bytes and bytes1[]

Both are dynamic types that store byte values, and in both cases, bytes are accessed by their index. However, the key difference lies in how the byte values are stored.

Consider the following contracts which stores the same byte value for both type bytes and bytes1[]:

contract Bytes {
    bytes foo_bytes = hex"ffeedd";

    // helper to get slot value
    function getSlotValue() public view returns (bytes32 x) {
        assembly {
            x := sload(0)
        }
    }
}

contract Bytes1Array {
    bytes1[] bar_bytes = [bytes1(hex"ff"), bytes1(hex"ee"), bytes1(hex"dd")];

    // helper to get slot value
    function getSlotValue() public view returns (bytes32 x) {
            bytes32 _slot = keccak256(abi.encode(0));
        assembly {
            x := sload(_slot)
        }
    }
}

Since the value assigned to the foo_bytes variable is a short bytes sequence (i.e., ≤ 31 bytes), both the value and its length (number of bytes * 2) are stored in the same storage slot (base slot), like so:

$\texttt{0x}\textcolor{green}{\texttt{ffeedd}}\texttt{000000000000000000000000000000000000000000000000000000000}\textcolor{orange}{6}$

On the other hand, the bar_bytes variable, which is of type bytes1[] (a dynamic array), stores the length of the array and values in separate slots:

The length is stored in the base slot:

$\texttt{0x000000000000000000000000000000000000000000000000000000000000000}\textcolor{orange}{3}$

The values are stored in the hash of the base slot:

$\texttt{0x0000000000000000000000000000000000000000000000000000000000}\textcolor{yellow}{\texttt{ddeeff}}$

In other words, bytes type with a short sequence uses less storage slots than bytes1[]. However, for sequences longer than 31 bytes, bytes type uses the same slot calculation as bytes1[], resulting in the same number of slots used.

Another difference between bytes and bytes1[] is how their values are stored in slots. For foo_bytes, the entire value is placed in its slot(s) at once. In contrast, for bar_bytes, the first element is stored in the least significant byte, followed by the next element, and this pattern continues until the last byte.

The animation shows how the new values assigned to foo_bytes and bar_bytes variable takes up two slots each (slots in green and yellow), with foo_bytes taking slot 0 and bar_bytes taking slot 1:

Struct

Structs in Solidity allow us to group multiple variables of different data types under a single name and use it as a new type. For instance, if we need a contract to store player information such as playerId, score, and level, using a struct would be the ideal choice. This way, we can group all the relevant details about each player in a single, organized structure.

Storage Slot in Struct

A struct in Solidity acts as a container for variables, and the storage slot allocation for each field within a struct follows the same rules we have discussed earlier.

Let’s see an example:

contract MyStruct {
        // Define a Player struct
    struct Player {
        address playerId;
        uint256 score;
        uint256 level;
    }

    uint256 private someNumber = 99; 

    /*
    AFTER DIFFERENT DECLARATIONS ABOVE, THE NEXT AVAILABLE SLOT IS: 6
    */

    // Declare a state variable of type Player
    Player private thePlayer;
}

Without running the code, can you guess the value in slot 0? If you think it’s 99, you are correct. This is because defining a struct in Solidity does not take up a storage slot space until it is declared, so the compiler sees the someNumber variable as the first storage variable.

Declare a Variable Of Player Struct Type:

Let’s examine how storage works with structs, first by declaring a struct — this will cause it to actually take up storage. Note that we are declaring it, not defining it like we did earlier.

/*
AFTER DIFFERENT DECLARATIONS ABOVE, THE NEXT AVAILABLE SLOT IS: 6
*/

// Declare a state variable of type Player
Player private thePlayer;

The fields within the Player struct will occupy three consecutive storage slots, starting from the base slot when declared. The playerId field, which is of type address, uses 20 bytes out of the 32 bytes available in a slot. The score and level fields, being of type uint256, each occupy a full slot space of 256 bits (32 bytes). With this known, we can say the storage slots for the fields are 6, 7 and 8 respectively.

Storage Slot Allocation For Dynamic Types Within a Struct

Another example is having dynamic types within a struct. Let’s modify the previous example to use mappings and also assign some values to it:

contract MyStruct {
        // Define a Player struct
    struct Player {
        address playerId;
        mapping(uint256 level => uint256 score) playerScore;
    }

    uint256 private someNumber = 23; // storage slot 0
    uint256 private someNumber1 = 77; // storage slot 1

    // Declare a state variable of type Player
    Player private thePlayer;

    constructor () {
        // Set deployer's address as player's id
        thePlayer.playerId = msg.sender;

        // Set player's score to 100 for level 1 and 68 for level 2
        thePlayer.playerScore[1] = 100;
        thePlayer.playerScore[2] = 68;
    }
}

The steps to calculating the storage slot for a value in the mapping within the struct are:

1. Identify the base slot of the thePlayer struct: this slot is determined when the struct is declared in the contract.
2. Calculate the slot for the playerScore mapping within the struct: this slot is determined by the order in which the mapping is declared in the struct.
3. Hash the concatenation of the key and mapping’s base slot, that is, the slot gotten in step 2.

With these steps known, we can calculate the storage slot holding the player score for level 2.

Step 1: Identify the base slot of the thePlayer

• thePlayer is a struct declared in the contract above, and since it is declared after someNumber and someNumber1 variable, its base slot will be slot 2 (because someNumber occupies slot 0 and someNumber1 occupies slot 1).

Step 2: Calculate the slot for the playerScore mapping within the struct

// Define a Player struct
struct Player {
     address playerId;
     mapping(uint256 level => uint256 score) playerScore;
}

• Starting from the struct’s base slot (slot 2), each fields are assigned slot sequentially. This means the first field playerId of type address, occupies the slot 2 (base slot), while the second field playerScore mapping, is placed in the next slot, which is slot 3 (the mapping’s base slot).

Step 3: Hash the concatenation of the key and the mapping’s base slot

• With the key and the mapping’s base slot known, we can calculate our target storage slot by concatenating and hashing them.

  The following image shows how the target slot (green box) is determined by passing the right key (in this case, a level 2) and the mapping’s base slot (3), then sload-ing the target slot: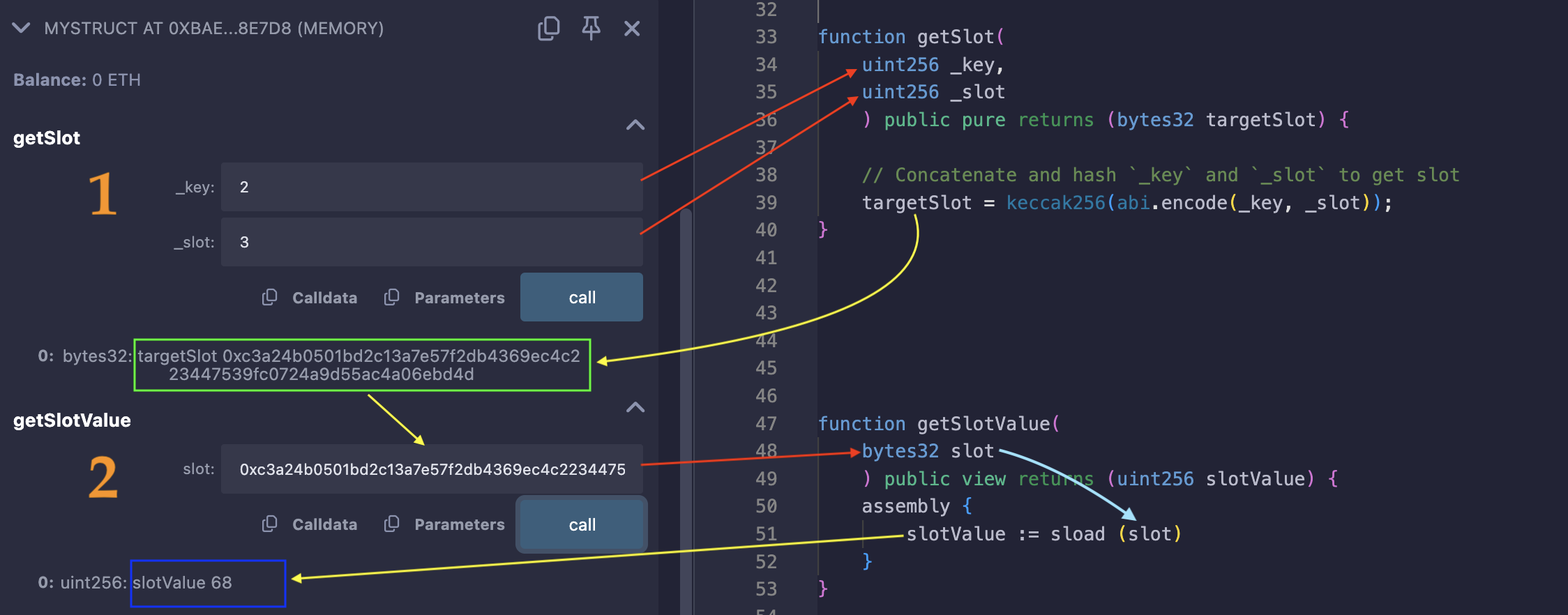

  

In the blue box, is the returned value (the player’s score for level 2) from sload-ing the target slot.