Interest Bearing Token Part 1
The Token-2022 interest-bearing extension enables a token mint to automatically accrue interest on all token accounts for that specific mint. It uses an annual rate defined in the mint’s on-chain configuration.
However, this interest is a computed view: the actual token balance never changes on-chain. Instead, wallets and applications apply a continuous compounding formula to each user’s on-chain balance to compute their balance net of interest accrued. The developer can combine the computed interest and the on-chain balance into a single value or display them separately.
This extension provides the accounting mechanism for accruing interest; it relies on separate DeFi applications to provide economic backing for the interest.
In this article, we’ll break down the architecture of the interest-bearing extension, explain the mathematics behind the calculations, cover wallet compatibility, and walk through a practical implementation example with Anchor.
Interest-bearing extension architecture
As we discussed in our Token-2022 article, token extensions are modular features added to a mint or token account. A mint account’s base layout is 82 bytes, and a token account’s base layout is 165 bytes. Extension data is appended after those base sizes, so you must allocate space equal to the base size plus the size of any enabled extensions before creating mint or token account.
The allocated space for the interest-bearing extension stores the extension’s data, including an authority account field that can update the interest rates. If the authority account field is all zeros, it is treated as None, which means the interest rate remains immutable. In practice, the authority can be set to a DeFi application, which then sets the interest rate to reflect actual economic activity in the app.
In addition to the authority field, the Rust struct below (which we’ve taken directly from the source code for the extension) defines the complete interest-bearing extension data:
- The initialization timestamp (
initialization_timestamp), which serves as the starting time for all interest calculations - The average interest rate (
pre_update_average_rate) since initialization until the last time the rate was updated. - The last change in interest rate timestamp (
last_update_timestamp), used to calculate accrued interest - The current interest rate (
current_rate) applied since the last update timestamp.
/// Annual interest rate, expressed as basis points
pub type BasisPoints = PodI16;
const ONE_IN_BASIS_POINTS: f64 = 10_000.;
const SECONDS_PER_YEAR: f64 = 60. * 60. * 24. * 365.24;
pub struct InterestBearingConfig {
/// Authority that can set the interest rate and authority
pub rate_authority: OptionalNonZeroPubkey,
/// Timestamp of initialization, from which to base interest calculations
pub initialization_timestamp: UnixTimestamp,
/// Average rate from initialization until the last time the rate was updated
pub pre_update_average_rate: BasisPoints,
/// Timestamp of the last update, used to calculate the total amount accrued
pub last_update_timestamp: UnixTimestamp,
/// Current rate, since the last update
pub current_rate: BasisPoints,
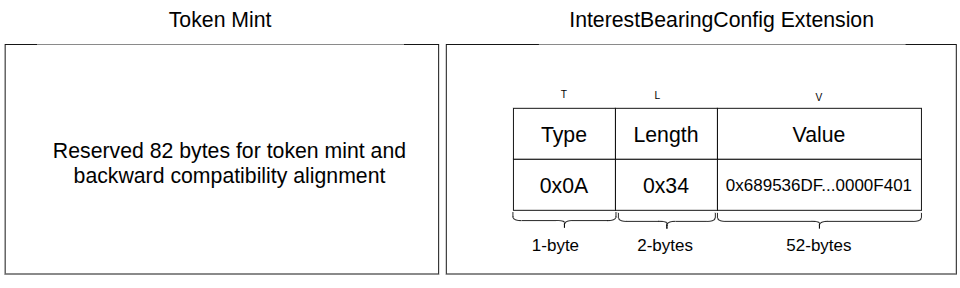
}Type-Length-Value (TLV) layout of the interest-bearing extension
All Token-2022 extensions follow a Type-Length-Value (TLV) format, which allows programs to easily read and skip over different extension data stored in an account.
The InterestBearingConfig TLV entry is encoded as:
- T (
type):0x0A(the type identifier forInterestBearingConfig) - L (
length):0x34(u8, value = 52 decimal) - V (
value): serialized fields concatenated in order:rate_authority(32 bytes)initialization_timestamp(8 bytes)pre_update_average_rate(2 bytes)last_update_timestamp(8 bytes)current_rate(2 bytes)
The fields pre_update_average_rate and current_rate are not stored as floating-point numbers. Instead, they are stored as basis points.
1 basis point = 1/100 (0.01%)
So, to represent an annual interest rate of 2.50%, you would store the integer 250 (because 250 basis points is 250*1/100=2.5%) in the current_rate field. To convert from a percentage into basis points, simply divide by 0.01 (or equivalently, multiply by 100). In this example, 2.5 / 0.01=250.
In the InterestBearingConfig extension TLV layout, the V portion is the serialized value of all extension fields concatenated in order, as explained previously in our Token-2022 article.
For example, suppose the extension contains the following values:
rate_authority:7xKXtg2CW87d9LN6HBUtjQVSiJ9MCrgdGubbyiTZRjrwb(32 bytes)initialization_timestamp:1672531200(Jan 1, 2023; 8 bytes)pre_update_average_rate:500(5.00% in basis points; 2 bytes)last_update_timestamp:1704067200(Jan 1, 2024; 8 bytes)current_rate:500(5.00% in basis points; 2 bytes)
When we concatenate the above fields as a single continuous byte sequence, the V (hex) portion of the TLV is:
0x689536DF68C2FB0A61A08DEDC9797145C969328A05D68A2A8C06E15A3AB6BD5200CDB06300000000F4018000926500000000F401The full TLV entry is T(0x0A) | L(0x34) | V(...) and is appended immediately after the Mint account’s data.
Interest bearing extension initialization
The interest-bearing extension is enabled and initialized in a single operation, which both reserves space and writes the extension’s TLV. As we discussed previously in the Token-2022 article,
other extensions usually require two steps:
- Enable required extensions and reserve space for the extension
- And a separate initialize instruction to configure it.
Interest calculation model
Suppose you have a savings account at the bank. When you deposit $1,000 at 3% annual interest rate, your account statement doesn’t show your bank minting new dollars every day. Instead, the bank’s system calculates how much your balance would have grown if it were compounding and shows you the updated figure whenever you log in.
The interest-bearing extension makes your mint account work in a similar way. Your balance on-chain (the equivalent of your bank’s balance) never changes from $1,000. But your wallet (like the online banking app) uses a compounding formula to display ****$1,015 after six months or $1,030 after a year.
If the bank later raises your rate to 5% from 3%, future interest compounds faster, but your previous year at 3% is still “locked in”, and the final balance will properly reflect the 3% growth rate for that time period.
The interest-bearing extension uses the continuous compound interest formula ($A = P × e^{rt}$ ) to calculate the interest and ensure that your accrued yield is accurate whether the rate changes or not (we explore this formula in detail later).
The formula is hard-coded into the Token-2022 program in two variations: before and after the most recent rate update.
The before variation captures growth under the earlier rate (in case the authority updates the rate), while the after variation captures growth under the current rate. Together, they produce a continuous, time-weighted compounding factor that ensures balances stay accurate across multiple rate changes.
Next, let’s show how these operations are computed mathematically with an example.
How the interest-bearing extension uses the continuous compound interest formula
$$ A = P × e^{rt}$$
First off, here is a description of the variables in the formula:
- A = the final amount (principal + interest)
- P = the principal (initial amount)
- e = Euler’s number (approximately 2.71828…)
- r = the annual interest rate (as a decimal)
- t = time in years (Token-2022 internally works with seconds)
$$ t = \frac{elapsed\_seconds}{SECONDS\_PER\_YEAR}$$
Where SECONDS_PER_YEAR = 60 × 60 × 24 × 365.24
Take the following example for a scenario where the rate has not been changed:
- You deposit 1000 tokens (P = 1000)
- Interest rate is 5% (r = 0.05)
- After 1 year (t = 1).
- The displayed balance is calculated as:
$$ A = 1000 \times e^{0.05 \times 1} = 1000 \times 2.718^{0.05} \approx 1051.27 \text{ tokens}$$
Let’s also show the behavior when the rate changes
Now suppose the interest rate starts at 3% but increases to 5% after the first 3 months. Token-2022 handles this by splitting the calculation into segments.
Note: In our mathematical model, we represent three months as 0.25 (calculated as 3 ÷ 12 = 0.25)
-
Pre-update growth:
Let’s start by calculating the elapsed time (t).
$$ t_1 = \frac{3\text{ months}}{12\text{ months}} = 0.25$$
If we substitute the t in the formula to 0.25 years from our calculation above, we’ll get the result below:
$$ A_1 = 1000 \times e^{0.03 \times 0.25} =1000*1.007528 \approx 1007.53 \text { tokens}$$
-
Post-update growth:
New rate = 5% (r₂ = 0.05)
Remaining elapsed time = 9 months which is calculated as 9/12 (t₂ = 0.75)
$$ A_2 = A_1 \times e^{0.05 \times 0.75} = 1007.53 \times 1.0382 \approx 1046.027 \text{ tokens}$$From our calculation so far, you’ll notice that the interest represents a one-year yield. In the first three months (pre-update growth period), the user earned 7.53 tokens at a 3% rate, bringing their total to 1,007.53 tokens. When the rate increased to 5% for the remaining nine months (the post-update growth period), they earned an additional 38.5 tokens, resulting in a final balance of 1,046.03 tokens.
Handling multiple interest rate updates
We’ve seen how this calculation works for two time period, but the interest-bearing extension can update the interest rate several times during a token’s lifetime. Each update ensures the accrued yield remains consistent with all past and future rate change.
When a new rate is set, the program updates the fields in the InterestBearingConfig as follows:
- It recalculates
pre_update_average_rateas a time-weighted average of all previous rates, including the one that was just replaced. - It moves
last_update_timestampforward to the current block time. - It sets
current_rateto the new rate value (for example,700basis points for 7%).
Mathematically, we can recalculate the new time-weighted average (pre_update_average_rate) of all previous rates with the formula below:
$$ pre\_update\_average\_rate_{new} = \frac{(r_1 \times t_1) + (r_2 \times t_2)}{t_1 + t_2}$$
where:
- r₁ →
pre_update_average_rate(the previous average rate) - t₁ →
last_update_timestamp - initialization_timestamp(elapsed time under all previous rates) - r₂ →
current_rate(the most recent rate before the update) - t₂ →
current_timestamp - last_update_timestamp(elapsed time under the current rate)
Example calculation of the time weighted average
Suppose we start with:
initialization_timestamp = 0pre_update_average_rate = 300(3%)last_update_timestamp = 7889184seconds (~3 months. TheInterestBearingConfigextension stores absolute Unix timestamps, but in this example, we use a 3-months elapsed duration in seconds to illustrate the interest growth, since interest depends only on the passage of time, not the specific timestamp values)current_rate = 500(5%)current_timestamp = 31556736(≈ 1 year)new_rate = 700(7%)
Then:
$$ pre\_update\_average\_rate_{new} = \frac{(300 \times 7889184) + (500 \times 23667552)}{31556736} \approx 450$$
After the update:
pre_update_average_rate = 450(4.50%)last_update_timestamp = 31556736current_rate = 700(7%)
Code illustration of the formula
The pre-update growth period and the post-update growth period ****are implemented as the pre_update_exp and post_update_exp functions in the extension’s source code. The portion defines both functions is shown below.
The pre_update_exp and post_update_exp functions directly implement the continuous compound interest formula ($A = P × e^{rt}$), specifically, the interest growth factor ( $e^{rt}$) for two different time periods — before and after the most recent interest rate update.
pre_update_expcalculates the compound interest growth for the time between the token’s initialization and the last rate update.- It multiplies the average rate during that period (
pre_update_average_rate) by the elapsed time in seconds. $numerator=r_{pre}×t_{pre(seconds)}$ - It divides the numerator by both:
- the number of seconds in a year (
SECONDS_PER_YEAR) to convert time from seconds to years, and - the constant
ONE_IN_BASIS_POINTS(which equals 10,000) to convert the rate from basis points to a decimal.
$\text{exponent} = \frac{\text{numerator}}{60 \times 60 \times 24 \times 365.24 \times 10{,}000}$
- the number of seconds in a year (
- Finally, it computes
exponent.exp()which is the continuous growth factor (Euler’s number raised to the power of the exponent) for that duration. This is represented mathematically as $e^{rt}$.
- It multiplies the average rate during that period (
post_update_expperforms the same computation but uses the current rate (current_rate) and the time elapsed since the most recent update (post_update_timespan).
Below are the functions pre_update_exp and post_update_exp from the Token-2022 codebase:
pub struct InterestBearingConfig {
/// Authority that can set the interest rate and authority
pub rate_authority: OptionalNonZeroPubkey,
/// Timestamp of initialization, from which to base interest calculations
pub initialization_timestamp: UnixTimestamp,
/// Average rate from initialization until the last time it was updated
pub pre_update_average_rate: BasisPoints,
/// Timestamp of the last update, used to calculate the total amount accrued
pub last_update_timestamp: UnixTimestamp,
/// Current rate, since the last update
pub current_rate: BasisPoints,
}
fn pre_update_exp(&self) -> Option<f64> {
let numerator = (i16::from(self.pre_update_average_rate) as i128)
.checked_mul(self.pre_update_timespan()? as i128)? as f64;
let exponent = numerator / SECONDS_PER_YEAR / ONE_IN_BASIS_POINTS;
Some(exponent.exp())
}
fn post_update_exp(&self, unix_timestamp: i64) -> Option<f64> {
let numerator = (i16::from(self.current_rate) as i128)
.checked_mul(self.post_update_timespan(unix_timestamp)? as i128)? as f64;
let exponent = numerator / SECONDS_PER_YEAR / ONE_IN_BASIS_POINTS;
Some(exponent.exp())
}
fn post_update_timespan(&self, unix_timestamp: i64) -> Option<i64> {
unix_timestamp.checked_sub(self.last_update_timestamp.into())
}
To compute the precise compounded interest—regardless of whether the rate has changed—the interest-bearing extension uses the total_scale function.
It multiplies the results of pre_update_exp and post_update_exp, which represent the growth factors before and after the last rate update, respectively.
The product gives the total exponential growth factor across both time segments.
Finally, the total_scale function divides the result by 10^decimals to scale the value into the token’s standard precision. For example, the SOL token has 9 decimals, so the result of pre_update_exp and post_update_exp will divide by 10^9 .
The resulting value of total_scale is the scaling factor applied to the on-chain balance to display the continuously compounding interest accurately.
fn total_scale(&self, decimals: u8, unix_timestamp: i64) -> Option<f64> {
Some(
self.pre_update_exp()? * self.post_update_exp(unix_timestamp)?
/ 10_f64.powi(decimals as i32),
)
}In other words, the resulting value of every interest calculation in the interest-bearing extension is the product of the principal and total_scale.
How the interest-bearing extension applies the formula internally
Here are the three important fields that make this calculation possible internally:
pre_update_average_rate: Stores the cumulative growth factor (the exponent from the formula) up until the last rate update. In our example, after 3 months this captures0.03 × 0.25 = 0.0075.last_update_timestamp: Marks the exact time the last rate update happened. In the example, this is the timestamp at the 3-month mark.current_rate: The interest rate currently in effect. In the example, this switches from0.03to0.05after 3 months.
When a wallet or program queries the balance, the interest-bearing extension reconstructs the formula as:
$$ A=P×e^{(pre\_update\_average\_rate+current\_rate×(t−last\_update\_timestamp))}$$
This is equivalent to what we have in the total_scale function we mentioned earlier:
fn total_scale(&self, decimals: u8, unix_timestamp: i64) -> Option<f64> {
Some(
self.pre_update_exp()? * self.post_update_exp(unix_timestamp)?
/ 10_f64.powi(decimals as i32),
)
}UI display balance conversion functions
The interest-bearing extension exposes two functions that wallets and apps use to display balances consistently off-chain:
- The function converting raw amount to UI amount (
amount_to_ui_amount), which first computes the accrued interest (token amount * total scale), then formats the result into a string with the given decimal precision and removes unnecessary zeroes.
/// Convert a raw amount to its UI representation using the given decimals
/// field. Excess zeroes or unneeded decimal point are trimmed.
pub fn amount_to_ui_amount(
&self,
amount: u64,
decimals: u8,
unix_timestamp: i64,
) -> Option<String> {
let scaled_amount_with_interest =
(amount as f64) * self.total_scale(decimals, unix_timestamp)?;
let ui_amount = format!("{scaled_amount_with_interest:.*}", decimals as usize);
Some(trim_ui_amount_string(ui_amount, decimals))
}- and the
try_ui_amount_into_amount, which converts a UI balance (the one that includes the computed interest) back into the raw amount (without the interest) used internally. Here is the original implementation in the interest-bearing source code.
/// Try to convert a UI representation of a token amount to its raw amount
/// using the given decimals field
pub fn try_ui_amount_into_amount(
&self,
ui_amount: &str,
decimals: u8,
unix_timestamp: i64,
) -> Result<u64, ProgramError> {
let scaled_amount = ui_amount
.parse::<f64>()
.map_err(|_| ProgramError::InvalidArgument)?;
let amount = scaled_amount
/ self
.total_scale(decimals, unix_timestamp)
.ok_or(ProgramError::InvalidArgument)?;
if amount > (u64::MAX as f64) || amount < (u64::MIN as f64) || amount.is_nan() {
Err(ProgramError::InvalidArgument)
} else {
// this is important, if you round earlier, you'll get wrong "inf"
// answers
Ok(amount.round() as u64)
}
}The above functions (amount_to_ui_amount and try_ui_amount_into_amount) are not executed on-chain. They’re client-side helpers implemented in the Rust SDK (and also mirrored in the TypeScript SDK)
Wallet compatibility
Token-2022 extensions are not widely supported by wallets in the Solana ecosystem yet. Since the on-chain balance of an interest-bearing token never changes, a wallet must detect the interest-bearing extension on the mint and apply the compounding formula before displaying the user’s balance. Without this logic, the wallet will always show the raw principal amount and ignore the accrued growth.
This difference means two wallets can display the same account with different results: one showing only the fixed amount stored on-chain, the other showing the continuously compounding balance derived from the extension fields. Until wallets update their account rendering to include Token-2022 extensions, applications that rely on interest-bearing tokens will often need to compute and display balances themselves.
Conclusion
In the course of this article, we’ve discussed how the interest-bearing token extension work, how it introduces a way to represent yield directly at the token mint level without requiring on-chain balance updates or periodic distribution transactions.
We also discussed how all accruals happen through a deterministic formula off-chain, making the system efficient while still giving users the experience of a growing balance.
The mathematics behind the display ensures that the accrued interest compounds correctly, and wallet integrations can rely on the provided functions to keep balances consistent.
Support across wallets and explorers remains limited, so for now applications that adopt this feature must take responsibility for displaying balances correctly.
This article is part of a tutorial series on Solana.