Calculating the real reserves between two prices in the Uniswap V3 codebase

In previous chapters, we derived formulas to calculate the real reserves of tokens X and Y between two prices in a segment. These formulas are used by the protocol when users add or remove liquidity, as well as during swaps.

In this chapter, we show where these formulas are located in the codebase. Since the protocol stores square roots of prices in the Q64.96 format, the formulas must be adjusted to use this format.

Calculating the amounts $x_r$ and $y_r$ in the codebase

The codebase contains helper functions for calculating the amounts of tokens X and Y between two prices at constant liquidity. These functions are defined in the SqrtPriceMath.sol library with the following names:

• getAmount0Delta: Calculates the real reserves in X between two prices for a given liquidity.
• getAmount1Delta: Calculates the real reserves in Y between two prices for a given liquidity.

These formulas for real reserves actually depend on the square roots of prices, not on the prices themselves. We can recover the price from its square root by squaring the value—but this is only done off-chain; it is not necessary on-chain.

For brevity, we will continue to refer to prices, but the reader should be aware that the protocol only uses the square roots of prices. For instance, if the protocol needs to calculate the amount of real reserves between prices 100 and 200, it will call these functions with arguments $\sqrt{100}$ and $\sqrt{200}$ , both in Q64.96 format, instead of 100 and 200.

The functions getAmount0Delta and getAmount1Delta

The SqrtPriceMath library has two functions named getAmount0Delta, one of which has the following signature, the other will be discussed in a later chapter.

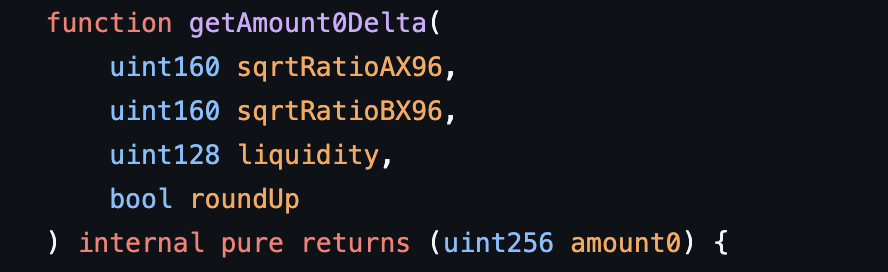
It receives two square roots of prices in Q64.96 format (sqrtRatioAX96 and sqrtRatioBX96), the liquidity, and a boolean (roundUp) that specifies whether the final amount should be rounded up or down.

The amount is rounded down when it represents a payment from the protocol to the user—such as in swaps or when removing liquidity—and rounded up when it represents a deposit from the user to the protocol—such as in swaps or when providing liquidity. Rounding always favors the protocol and disadvantages the user.

This function calculates and returns the amount of real reserves in tokens X between sqrtRatioAX96 and sqrtRatioBX96 for a given liquidity $L$, assuming that the liquidity in this segment is entirely in token X.

The protocol also has two getAmount1Delta functions, one of which has a signature very similar to getAmount0Delta, the other will be discussed in a later chapter. Its purpose is to calculate the amount of real reserves in tokens Y between sqrtRatioAX96 and sqrtRatioBX96, for a given liquidity $L$, assuming that the liquidity in this segment is entirely in token Y.

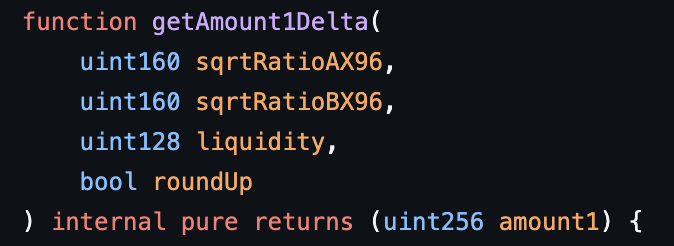
The same rounding behavior as getAmount0Delta applies to this function.

The interactive tool below calculates the same as getAmount0Delta and getAmount1Delta for a price interval, given liquidity. To use it, move the blue and purple sliders to adjust sqrtRatioAX96 and sqrtRatioBX96, and the orange slider to adjust the liquidity. The amount0/amount1 radio buttons indicate which function should be executed. To round up the result, select the roundUp checkbox.

Note that these functions assume that, between two price points, liquidity is constant and only consists of a single reserve.

We have to know that information in advance before we use these functions because these functions have no knowledge of the distribution of liquidity over the entire range of possible prices.

The function getAmount0Delta

The function getAmount0Delta calculates the following formula, which we derived in the chapter on real reserves:

$$ x_r=\frac{L}{\sqrt{p_a}}-\frac{L}{\sqrt{p_b}}$$

but using the square root of prices in Q64.96 format, given by sqrtRatioAX96 and sqrtRatioBX96.

Since the relation between $\sqrt{p}$ and sqrtRatioX96 is

$$ \sqrt{p}=\frac{\text{sqrtRatioX96}}{2^{96}}$$

we can substitute this relation in the formula for $x_r$ as follows

$$ \begin{align*} x_r &= \frac{L}{\boxed{\sqrt{p_a}}} – \frac{L}{\boxed{\sqrt{p_b}}}\\ x_r&=\frac{L}{\frac{\text{sqrtRatioAX96}}{2^{96}}} – \frac{L}{\frac{\text{sqrtRatioBX96}}{2^{96}}} && \text{substituting } \sqrt{p_a} \text{ and } \sqrt{p_b} \\ x_r&= \frac{L\cdot 2^{96}}{\text{sqrtRatioAX96}}-\frac{L\cdot 2^{96}}{\text{sqrtRatioBX96}} && \text{moved } 2^{96} \text{ to the numerator} \\ x_r&= \frac{ \color{orange}{L \cdot 2^{96}} \cdot \color{green}{(\text{sqrtRatioBX96} – \text{sqrtRatioAX96})}}{\text{sqrtRatioAX96} \cdot \text{sqrtRatioBX96}} && \text{finding a common denominator}\\ \end{align*}$$

The last step is not strictly mathematically necessary, but in code where division introduces a rounding error, it increases precision since we perform only one division instead of two.

This formula can be found in the function annotations in the codebase (without the $2^{96}$)

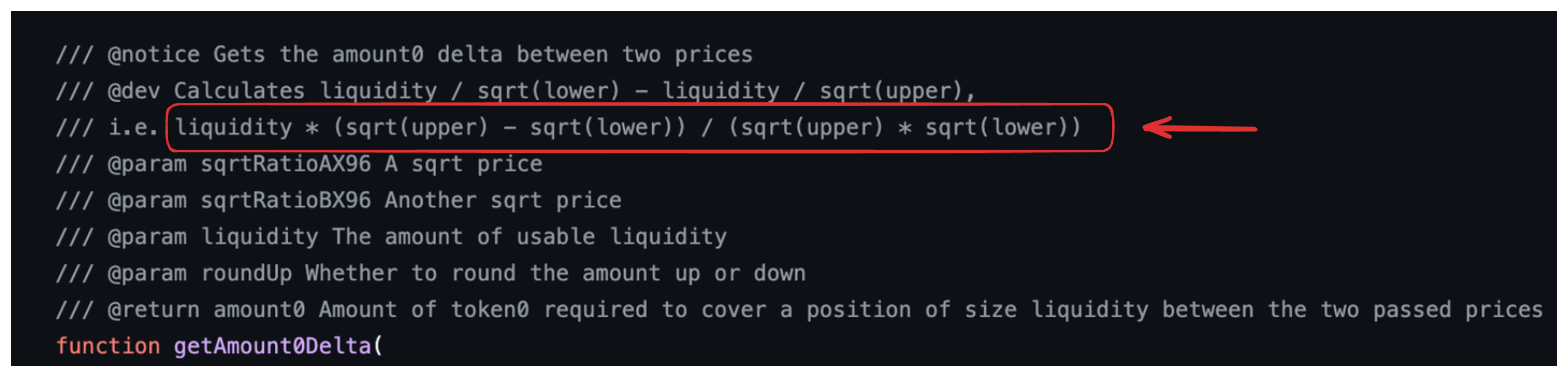
and is implemented in the function getAmount0Delta:

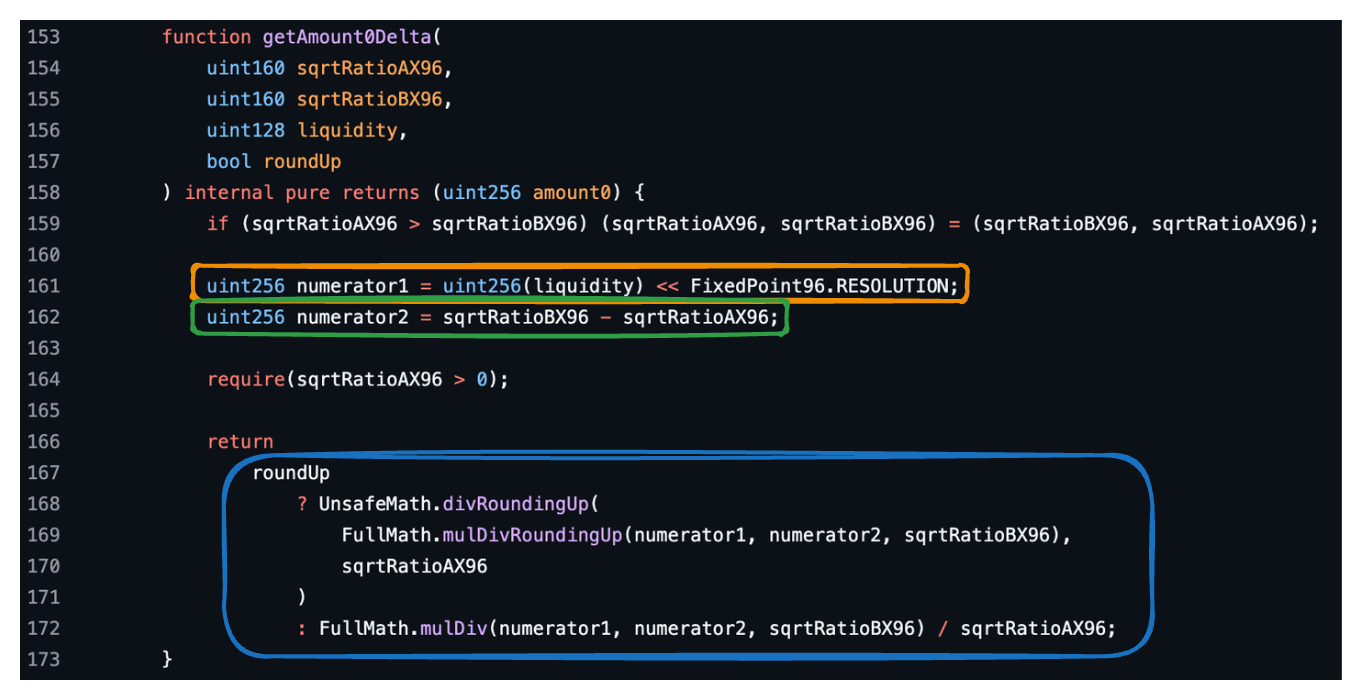
The orange and green boxes in the above image correspond to the orange and green parts of the formula we just derived, which make up the numerator. The blue box contains the complete expression, with the numerators terms multiplied and divided by both sqrtRatioAX96 and sqrtRatioBX96.

The mulDiv function multiplies the first two arguments and divides the product by the third. The mulDivRoundingUp function does the same, rounding up the final result.

The divRoundingUp performs integer division that rounds up.

As explained, the roundUp parameter indicates whether the final amount should be rounded up or not.

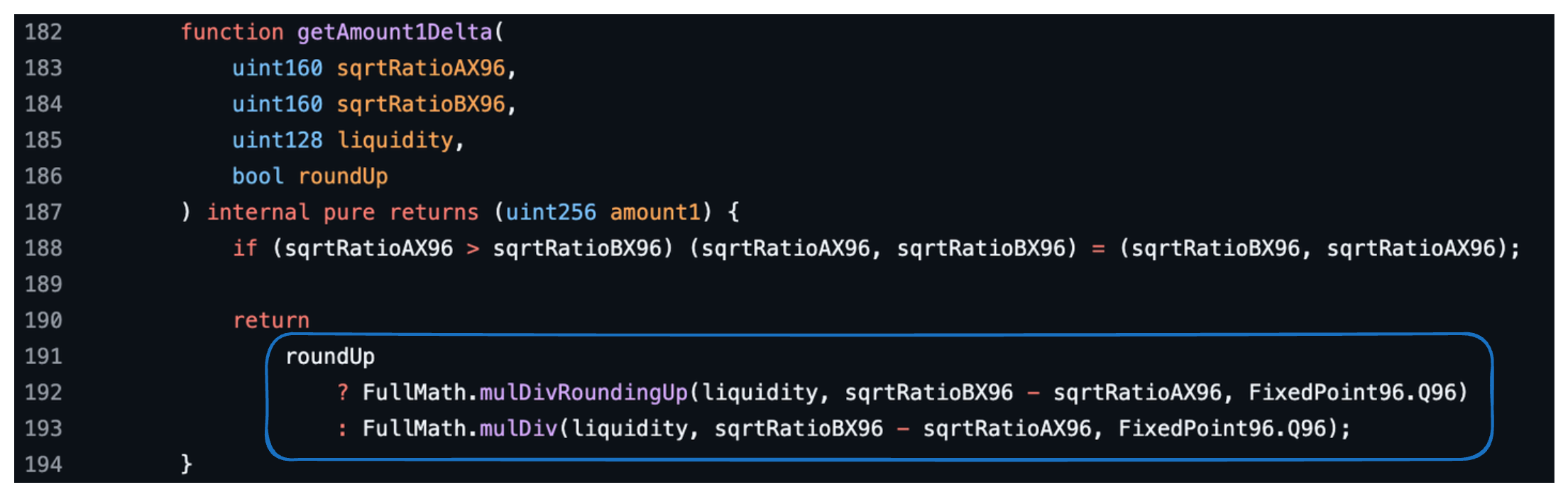
The functions getAmount1Delta

The goal of this function is to calculate the following formula

$$ y_r=L\sqrt{p_b} – L \sqrt{p_a}$$

but in terms of sqrtRatioAX96 and sqrtRatioBX96 instead of $\sqrt{p_a}$ and $\sqrt{p_b}$.

Remember that the relation between $\sqrt{p}$ and sqrtRatioX96 is

$$ \sqrt{p}=\frac{\text{sqrtRatioX96}}{2^{96}}$$

then we can use this relation in the formula for $y_r$ as

$$ \begin{align*} y_r &= L \boxed{\sqrt{p_b}} – L \boxed{\sqrt{p_a}} \\ y_r &= \frac{L \cdot \text{sqrtRatioBX96}}{2^{96}} – \frac{L \cdot \text{sqrtRatioAX96}}{2^{96}} \\ y_r &= \frac{L\cdot(\text{sqrtRatioBX96}-\text{sqrtRatioAX96})}{2^{96}} \end{align*}$$

Once again, we rearrange the formula to have only one division, which increases precision and matches what is found in the codebase.

The image below shows the function getAmount1Delta .

Functions getAmount0Delta and getAmount1Delta in Python

In this section, we’ll write the getAmount0Delta and getAmount1Delta functions in Python, which will be used to calculate the real reserves of a segment.

For simplicity, we won’t worry about rounding errors in the script.

They can be written as follows:

import math

def getAmount0Delta(sqrtRatioAX96, sqrtRatioBX96, liquidity, roundUp):
    numerator1 = liquidity*2**96
    numerator2 = sqrtRatioBX96 - sqrtRatioAX96
    if roundUp:
        return math.ceil(numerator1*numerator2 / (sqrtRatioBX96*sqrtRatioAX96))
    else: 
        return math.floor(numerator1*numerator2 / (sqrtRatioBX96*sqrtRatioAX96))        

def getAmount1Delta(sqrtRatioAX96, sqrtRatioBX96, liquidity, roundUp):
    if roundUp:
        return math.ceil(liquidity*(sqrtRatioBX96 - sqrtRatioAX96)/2**96)
    else:
        return math.floor(liquidity*(sqrtRatioBX96 - sqrtRatioAX96)/2**96)

Let’s say we want to calculate the real reserves between ticks -10 and 10, with the current price exactly at tick zero, as illustrated below. The real reserves in tokens Y are located between the lower tick (-10) and the current price (0), while the real reserves in tokens X are located between the current price (0) and the upper tick (10).

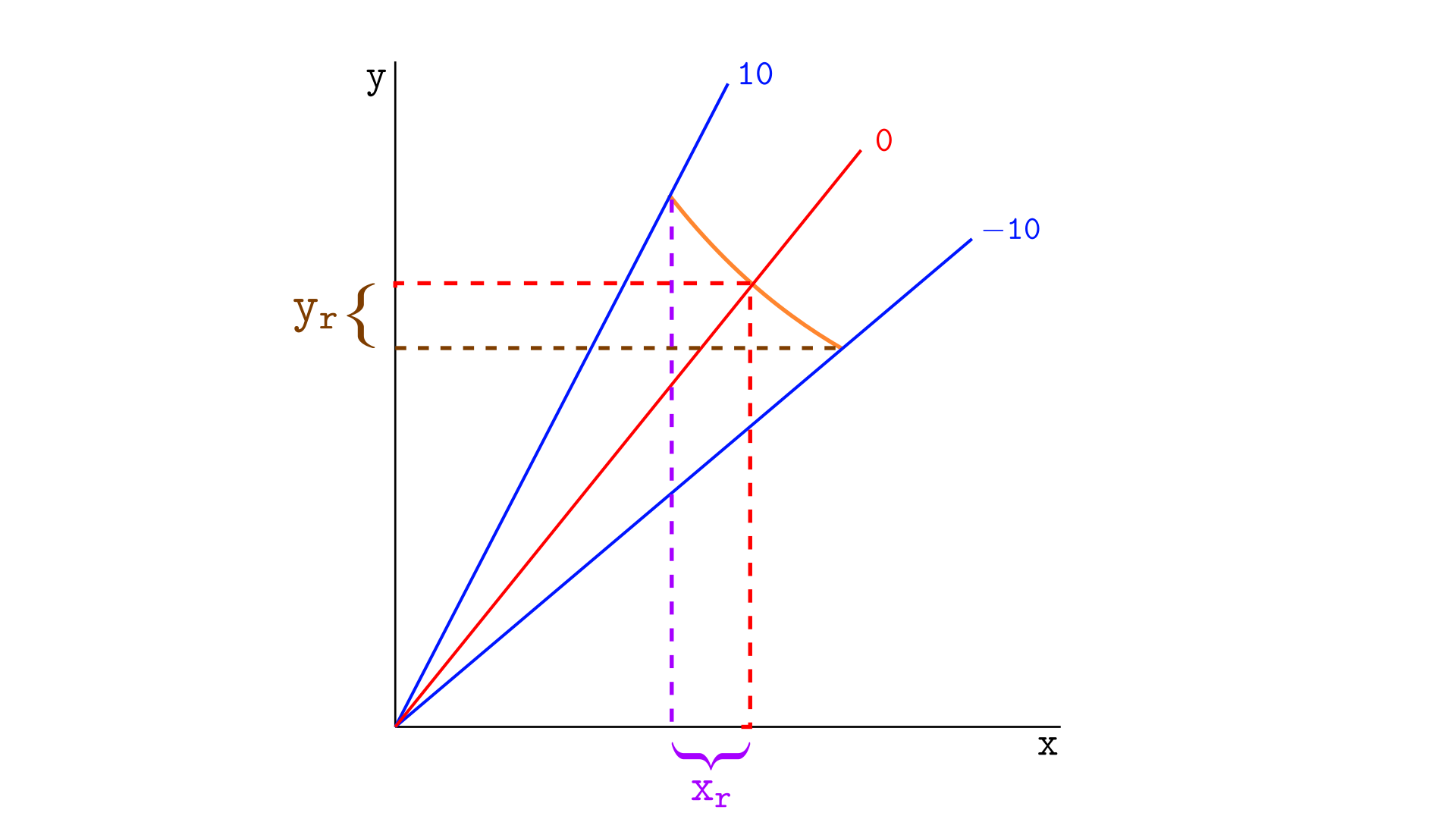
We can use the functions getAmount0Delta and getAmount1Delta to obtain these values.

To determine whether to round up or down, we need to consider the purpose of the calculation. If the calculation is for providing liquidity, the result will be rounded up, and vice versa for removing liquidity. Let’s do these calculations when providing liquidity, where rounding up is required.

The calculations and resulting values are shown in the code below.

def getSqrtRatioAtTick(i):
    return math.sqrt(1.0001 ** i) * 2**96;  

current_price = getSqrtRatioAtTick(0)
upper_price = getSqrtRatioAtTick(10)
lower_price = getSqrtRatioAtTick(-10)

print(getAmount0Delta(current_price, upper_price, 1000000000, True)) # 499851
print(getAmount1Delta(lower_price, current_price, 1000000000, True)) # 499851

Exercise: Calculate the real reserves between ticks -10 and 20 in the following cases:

1. The current price is at tick -20,
2. The current price is at tick 0,
3. The current price is at tick 20.

Conclusion

• The protocol provides functions to calculate the real reserves between two arbitrary prices, and a given constant liquidity between them. These functions are getAmount0Delta (for tokens X) and getAmount1Delta (for tokens Y).
• These functions receive prices as square roots in Q64.96 format, in variables called sqrtRatioAX96 and sqrtRatioBX96.
• The calculated amount of real reserves is rounded up if it represents an amount to be received by the protocol, and rounded down if it represents an amount to be paid by the protocol.

This article is part of a series on Uniswap V3.