Tick limits in Uniswap V3

The smallest tick in Uniswap v3 is -887,272 and the largest tick is 887,272. This chapter explains the rationale behind this range, which is based on finding the tick that corresponds to the highest price that can be stored in the protocol.

Price limit

In the previous chapter, we saw that the protocol stores the square root of the token price as fixed-point numbers of type Q64.96. This type of variable has a maximum whole number value of $2^{64}$. Consequently, the highest price it can store is $2^{128}$.

This means the protocol cannot handle prices greater than $2^{128}$. In other words, in Uniswap v3, a token can never reach a real price exceeding $2^{128}$. If this limit were not respected, the token could reach a price value that the protocol cannot not store.

Thus, the highest tick must be the tick corresponding to the price $2^{128}$ to be consistent with the highest price.

The highest tick index

To calculate the tick corresponding to the price $2^{128}$, let us remember that the relationship between prices and ticks is given by

$$ p(i)=1.0001^i $$

This relationship can be inverted by taking the base-1.0001 logarithm of both sides.

$$ \begin{align*} \log_{1.0001}(p(i)) &= \log_{1.0001}(1.0001^i) \\ \log_{1.0001}(p(i)) &= i \end{align*} $$

because $\log_b(b^x)= x$ for any base $b$.

The above formula allows us to calculate the tick index $i$ given the price $p(i)$.

Now, we need to determine the tick index relative to the highest possible token price, which is $2^{128}.$

Using $p(i) = 2^{128}$ in the formula above, we have that

$$ i=\log_{1.0001}(2^{128}) = 887272 $$

This calculation can be done in Python as

from math import log
log(2**128,1.0001) # log_1.0001(2**128) = 887272 

For this reason, tick index 887,272 is the highest used by the protocol, because ticks greater than 887,272 correspond to prices greater than the maximum value that can be stored by the sqrtPriceX96 variable.

The lowest tick index

The lowest tick index is set to -887,272, which is the negative of the highest possible tick.

This symmetry is desirable because the price of token X relative to token Y is the inverse of the price of token Y relative to token X. Thus, it is desirable to limit the minimum token price to $2^{-128}$, which corresponds to tick -887272.

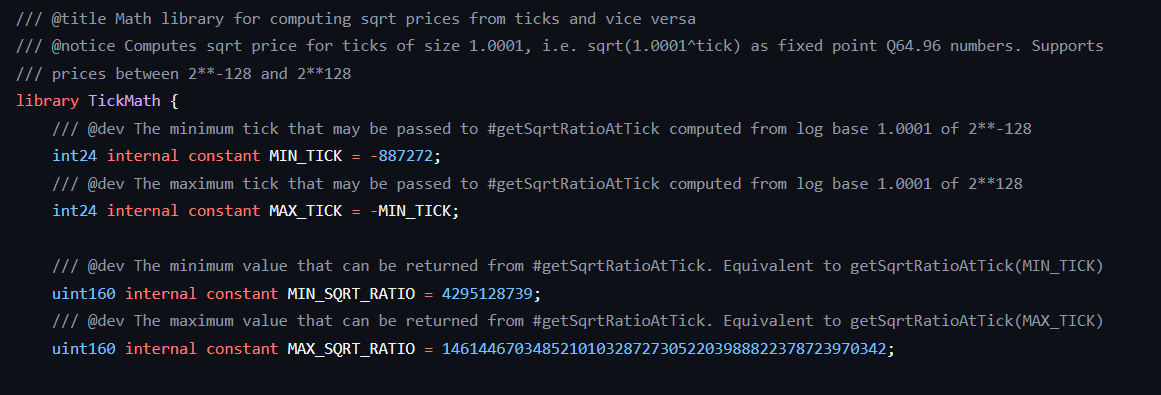
Minimum and maximum values in the codebase

The minimum and maximum ticks indexes are hardcoded as MIN_TICK and MAX_TICK in the Uniswap v3 TickMath library.

The minimum and maximum values the sqrtPriceX96 variable can assume are also hardcoded as MIN_SQRT_RATIO and MAX_SQRT_RATIO, respectively. This can be seen in the screenshot below, and these values will be calculated in a later section.

Ticks and the square root of the price

In the chapter Introducing ticks in Uniswap v3, we saw that ticks are defined by the following formula,

$$ p(i) = 1.0001^i $$

where $i$ are the tick indices.

It is possible to work with the square root of prices instead of the prices themselves, and to calculate the square root of the price for a given tick index.

To do this, simply take the square root of the formula above:

$$ \sqrt{p}= \sqrt{1.0001^i} = 1.0001^{\frac{i}{2}} $$

For instance, to calculate $\sqrt{p}$ for tick 100, we have $\sqrt{p}_{100}= 1.0001^{\frac{100}{2}} = 1.0001^{50} = 1.0050122696230506$. From this information, if we want to obtain $p_{100}$ (the price for tick 100), we just need to square it: $p_{100} = \left(\sqrt{p}_{100} \right)^2$.

Note that we disregarded the negative square root, keeping only the positive one, since prices cannot be negative. Therefore, we can always unambiguously retrieve the price by squaring the square root price.

The highest and lowest square root price in Q64.96 allowed in the protocol

The values for MIN_SQRT_RATIO and MAX_SQRT_RATIO can be calculated as follows:

The minimum tick index is -887,272, so the minimum allowed square root price is given by $\sqrt{p}_{−887272}$. This can be calculated as

$$ \sqrt{{p}}_{−887272} = 1.0001^{\frac{-887272}{2}} = 1.0001^{-443636} $$

To convert this value into fixed-point Q64.96, one needs to multiply it by $2^{96}$. Thus,

$$ \text{MIN\_SQRT\_RATIO} = 1.0001^{-443636} \times 2^{96} \approx 4295128738.152353 $$

One question that arises is: should we round up or round down this value? Let’s imagine that we round down, meaning the lowest possible value for the variable sqrtPriceX96 is 4295128738. In other words, it is possible for sqrtPriceX96 to reach the value of 4295128738.

This value, 4295128738, is slightly below tick -887272 (remember, the value associated with tick -887272 is 4295128738.152353). Thus, if the price reaches 4295128738, the current tick will be the closest tick, rounded down. In other words, it will be -887273. However, tick -887273 is not allowed, because we set tick -887272 as the minimum.

Therefore, we conclude that rounding up is necessary . That is, the smallest value that the sqrtPriceX96 variable can assume is 4295128739 , as it is hardcoded into the codebase.

This calculation can be done in Python as

math.ceil(1.0001**(-887272/2)*(2**96)) # 4295128739

The calculation for MAX_SQRT_RATIO is similar, but this time we use the highest possible value for the tick index, 887,272:

$$ \begin{align*} \text{MAX\_SQRT\_RATIO} &=\sqrt{p(887272)} \cdot 2^{96} \\ &= 1.0001^{\frac{887272}{2}} \cdot 2^{96} \\ &=1461446703485210103287273052203988822378723970342 \end{align*} $$

This calculation can be done in Python, but it will suffer from precision loss. In a later chapter, we will see how Solidity performs this kind of calculation exactly, without precision loss.

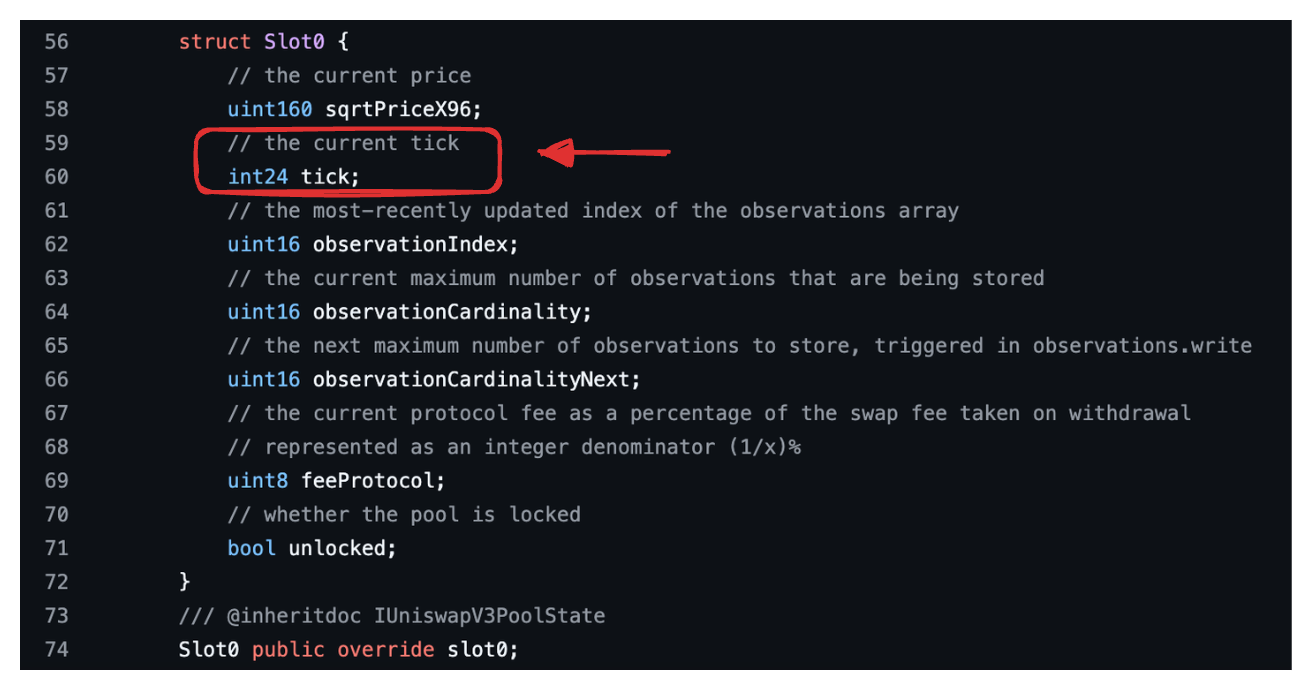
Why using int24 for tick indexes

The number of bits required to store 887,272 is $\log_2(887,272)\approx20$. Since we also have negative ticks, we need to store twice that amount of ticks. To hold both the original positive numbers and their negative values, our tick variable needs to support 21 bits.

Since Solidity only supports int sizes that are multiples of 8, this smallest int size that will hold all the ticks we need is int24. Therefore, Uniswap V3 uses an int24 to hold tick indexes (code link), as we can see below.

Summary

• Tick index $i$ can vary between -887,272 and 887,272. These ticks represent the lowest and highest prices a token can assume in the protocol, respectively $p(i)=1.0001^{}$ and $p(i)=1.0001^{887272}$.
• The MIN_SQRT_RATIO and MAX_SQRT_RATIO values represent the smallest and largest allowed square root prices in Q64.96 format, as defined by the protocol. These values are hardcoded in the codebase.