NTT Algorithm By Hand

The NTT (Number Theoretic Transform) algorithm converts a polynomial in a finite field from coefficient form to point form.

If a polynomial has degree $d$ then we evaluate it on the $k$-th roots of unity where $k\gt d.$

Rather than evaluating the polynomial $f(x)$ on each point in the set of $k$-th roots of unity, $\set{1,\omega,\omega^2,…,\omega^{k-1}}$, we use the image preservation theorem for multivalued functions to evaluate the multivalued function created by substituting $x$ in $f$ with $\sqrt[k]{x}$ on the domain $\set{1}$. We then iteratively expand the evaluations of the square root from $\set{1}$ to $\set{1,\omega^{k/2}}$ to $\set{1,\omega^{k/4},\omega^{k/2},-\omega^{k/4}}$ and so on until the evaluation is expanded to the $k$-th roots of unity.

The runtime of this method is $\mathcal{O}(n \log n)$.

Evaluating $f(x)=a_0+a_1x+a_2x^2+a_3x^3$ on the 4-th roots of unity

First, we factor the function to maximize the occurrences of $x^2$, since $2=k/2$ and $x^{k/2}$ is easy to evaluate on a root of unity (it only results in $\set{1,-1}$ depending on if the power of the root of unity is even or odd).

This creates the following function:

$$ f(x)=a_0+a_2x^2+x(a_1+a_3x^2)$$

Next, we transform $f$ so that $x\rightarrow\sqrt[4]{x}$ which gives us

$$ f(x)=a_0+a_2\sqrt{x}+\sqrt[4]{x}(a_1+a_3\sqrt{x})$$

Here is the square root expansion diagram:

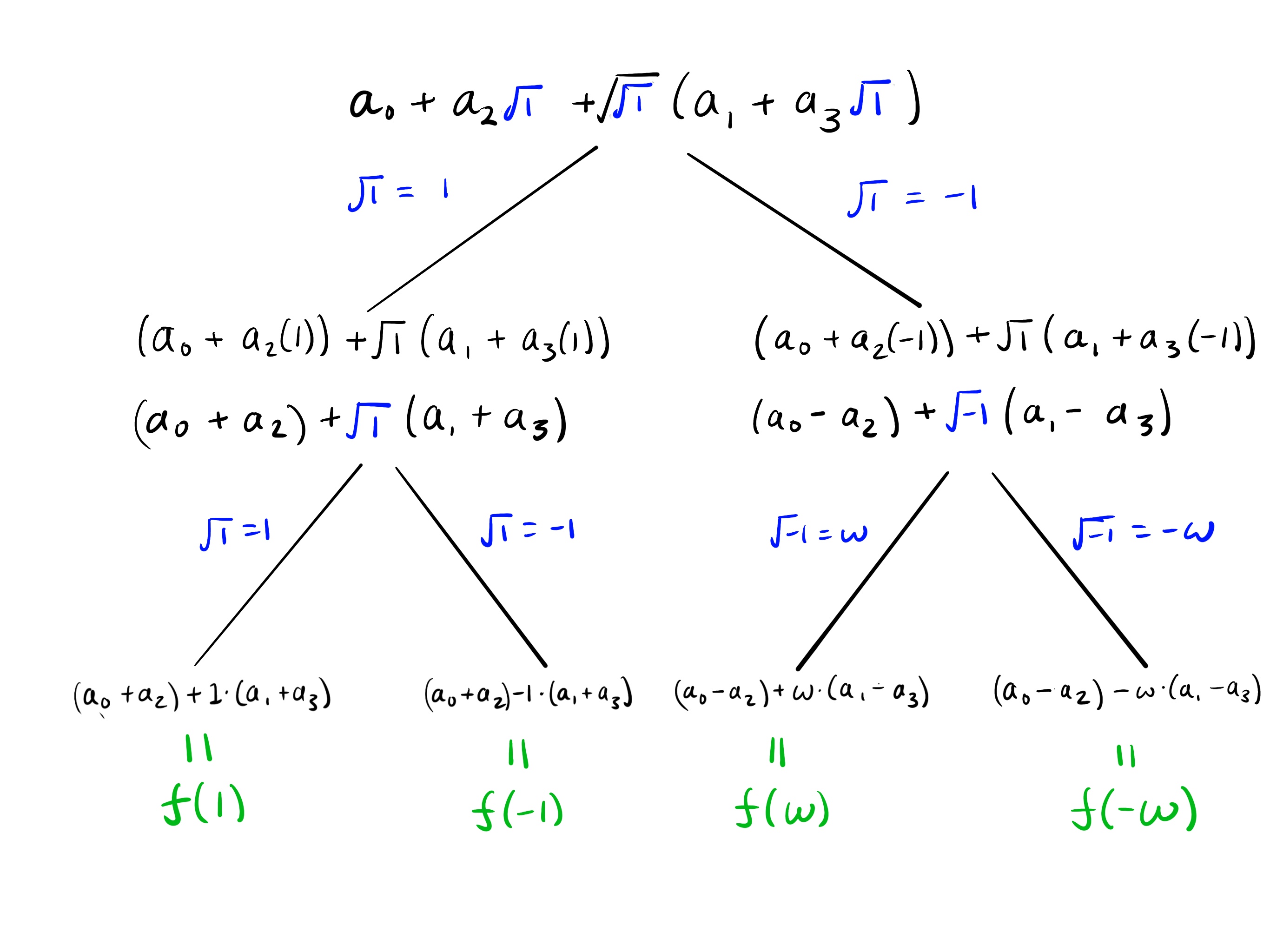
Now we compare the result to evaluating $f(x)$ on the 4-th roots of unity one-by-one:

$$ \begin{align*} f(1) &= a_0 &+& a_1(1) &+& a_2(1)^2 &+& a_3(1)^3\\ f(-1) &= a_0 &+& a_1(-1) &+& a_2(-1)^2 &+& a_3(-1)^3\\ f(\omega) &= a_0 &+& a_1(\omega) &+& a_2(\omega)^2 &+& a_3(\omega)^3\\ f(-\omega) &= a_0 &+& a_1(-\omega) &+& a_2(-\omega)^2 &+& a_3(-\omega)^3 \end{align*}$$

We have that $\omega^2=(-\omega^2)=-1$ and $\omega^3=-\omega$ and $(-\omega)^3=(-1)^3(\omega)^3=-\omega^3=-(-\omega)=\omega$. By substitution, we have:

$$ \begin{align*} f(1) &= a_0 &+& a_1 &+& a_2 &+& a_3\\ f(-1) &= a_0 &-& a_1 &+& a_2 &-& a_3\\ f(\omega) &= a_0 &+& a_1\omega &-& a_2 &-& a_3\omega\\ f(-\omega) &= a_0 &-& a_1\omega &-& a_2 &+& a_3\omega \end{align*}$$

Exercise: Use the above method to evaluate $a_0+a_1x+a_2x^2$ on the 4-th roots of unity. Hint: use the example above and set $a_3=0$.

The height of the tree is $\log n$ and we do $\mathcal{O}(n)$ operations on each row, so the runtime is $\mathcal{O}(n \log n)$.

Evaluating $f(x)=a_0+a_1x+…+a_7x^7$ on the 8-th roots of unity

First, we rearrange the polynomial to maximize the number of $x^4$ terms (since k = 8). This gives us:

$$ f(x)=a_0+a_4x^4+x^2(a_2+a_6x^4)+x((a_1+a_5x^4)+x^2(a_3+a_7x^4))$$

Now we substitute $x\rightarrow\sqrt[8]{x}$ to get our multivalued function $g(x)$

$$ g(x)=a_0+a_4\sqrt{x}+\sqrt[4]{x}(a_2+a_6\sqrt{x})+\sqrt[8]{x}((a_1+a_5\sqrt{x})+\sqrt[4]{x}(a_3+a_7\sqrt{x}))$$

Since drawing the evaluation tree in one image would be quite large, we’ll draw the left side of the tree where we evaluate $\sqrt{1}=1$ and show the diagram for that first:

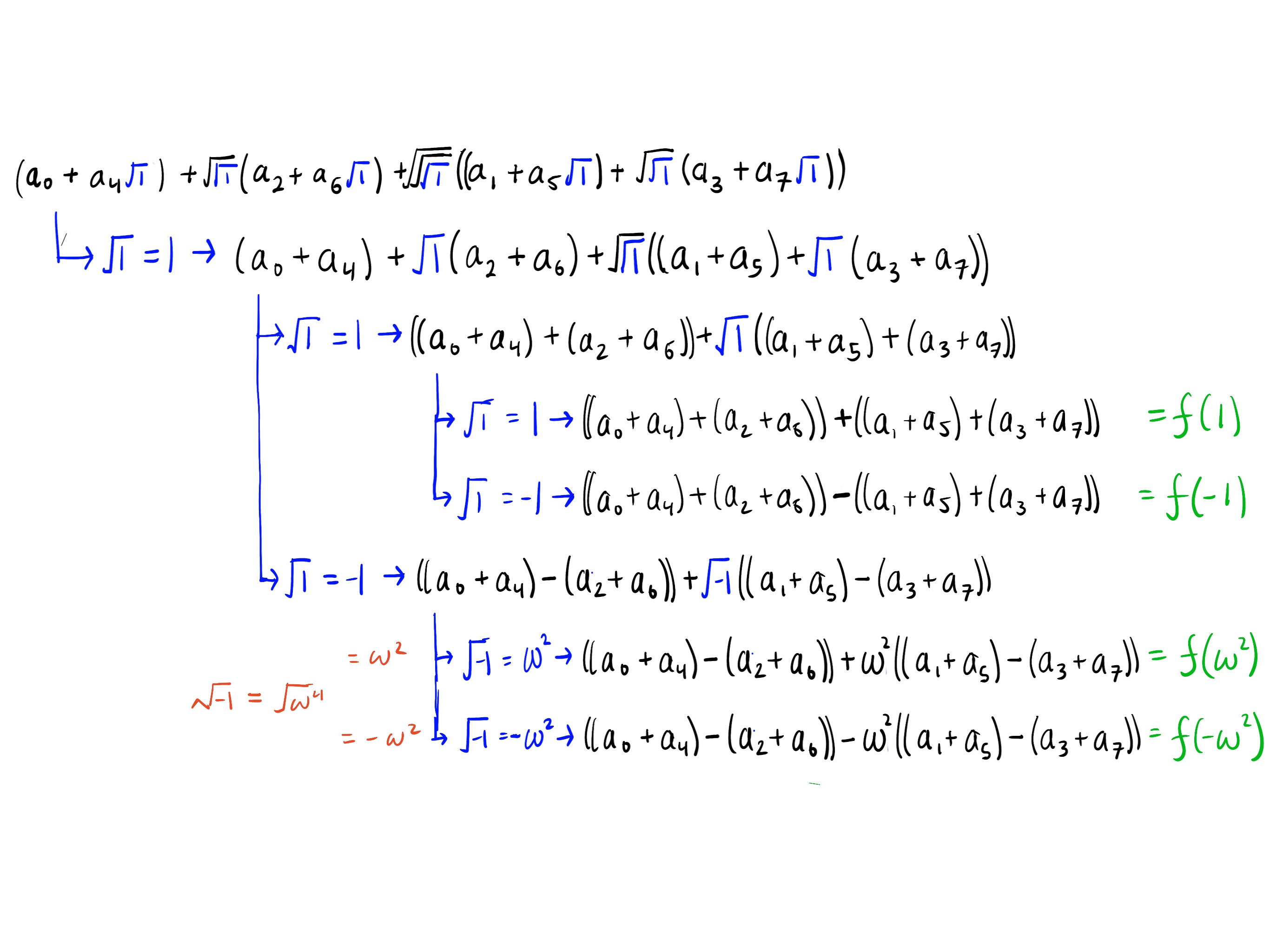
From the image above, we have that

$$ \begin{align*} f(1)=((a_0+a_4)+(a_2+a_6))+((a_1+a_5)+(a_3+a_7))\\ f(-1)=((a_0+a_4)+(a_2+a_6))+((a_1+a_5)+(a_3+a_7))\\ f(\omega^2)=((a_0+a_4)-(a_2+a_6))+\omega((a_1+a_5)-(a_3+a_7))\\ f(-\omega^2)=((a_0+a_4)-(a_2+a_6))-\omega((a_1+a_5)-(a_3+a_7))\\ \end{align*}$$

Now we expand the right side of the tree where $\sqrt{x}=-1$:

From that result, we have that:

$$ \begin{align*} f(\omega)=((a_0-a_4)+\omega^2(a_2-a_6))+\omega((a_1-a_5)+\omega^2(a_3-a_7))\\ f(-\omega)=((a_0-a_4)+\omega^2(a_2-a_6))-\omega((a_1-a_5)+\omega^2(a_3-a_7))\\ f(\omega^3)=((a_0-a_4)-\omega^2(a_2-a_6))+\omega^3((a_1-a_5)-\omega^2(a_3-a_7))\\ f(-\omega^3)=((a_0-a_4)-\omega^2(a_2-a_6))-\omega^3((a_1-a_5)-\omega^2(a_3-a_7)) \end{align*}$$

Combining the evaluations and distributing the omega terms, we have:

$$ \begin{align*} f(1) &= a_0 &+ a_4 &+ a_2 &+ a_6 &+ a_1 &+ a_5 &+ a_3 &+ a_7\\f(-1) &= a_0 &+ a_4 &+ a_2 &+ a_6 &- a_1 &- a_5 &- a_3 &- a_7\\f(\omega^2) &= a_0 &+ a_4 &- a_2 &- a_6 &+ a_1\omega^2 &+ a_5\omega^2 &- a_3\omega^2 &- a_7\omega^2\\f(-\omega^2)&= a_0 &+ a_4 &- a_2 &- a_6 &- a_1\omega^2 &- a_5\omega^2 &+ a_3\omega^2 &+ a_7\omega^2\\f(\omega) &= a_0 &- a_4 &+ a_2\omega^2 &- a_6\omega^2 &+ a_1\omega &- a_5\omega &+ a_3\omega^3 &- a_7\omega^3\\f(-\omega) &= a_0 &- a_4 &+ a_2\omega^2 &- a_6\omega^2 &- a_1\omega &+ a_5\omega &- a_3\omega^3 &+ a_7\omega^3\\f(\omega^3) &= a_0 &- a_4 &- a_2\omega^2 &+ a_6\omega^2 &+ a_1\omega^3 &- a_5\omega^3 &+ a_3\omega &- a_7\omega\\f(-\omega^3)&= a_0 &- a_4 &- a_2\omega^2 &+ a_6\omega^2 &- a_1\omega^3 &+ a_5\omega^3 &- a_3\omega & a_7\omega\end{align*}$$

Next, we put the coefficients in ascending order:

$$ \begin{align*} f(1) &= a_0 &+ a_1 &+ a_2 &+ a_3 &+ a_4 &+ a_5 &+ a_6 &+ a_7\\ f(-1) &= a_0 &- a_1 &+ a_2 &- a_3 &+ a_4 &- a_5 &+ a_6 &- a_7\\ f(\omega^2) &= a_0 &+ a_1\omega^2 &- a_2 &- a_3\omega^2 &+ a_4 &+ a_5\omega^2 &- a_6 &- a_7\omega^2\\ f(-\omega^2)&= a_0 &- a_1\omega^2 &- a_2 &+ a_3\omega^2 &+ a_4 &- a_5\omega^2 &- a_6 &+ a_7\omega^2\\ f(\omega) &= a_0 &+ a_1\omega &+ a_2\omega^2 &+ a_3\omega^3 &- a_4 &- a_5\omega &- a_6\omega^2 &- a_7\omega^3\\ f(-\omega) &= a_0 &- a_1\omega &+ a_2\omega^2 &- a_3\omega^3 &- a_4 &+ a_5\omega &- a_6\omega^2 &+ a_7\omega^3\\ f(\omega^3) &= a_0 &+ a_1\omega^3 &- a_2\omega^2 &+ a_3\omega &- a_4 &- a_5\omega^3 &+ a_6\omega^2 &- a_7\omega\\ f(-\omega^3)&= a_0 &- a_1\omega^3 &- a_2\omega^2 &- a_3\omega &- a_4 &+ a_5\omega^3 &+ a_6\omega^2 &+ a_7\omega \end{align*}$$

Now let’s rearrange the evaluations to go from $f(1)$, $f(\omega)$, … , $f(\omega^7)$

$$ \begin{align*} f(1) &= a_0 &+ a_1 &+ a_2 &+ a_3 &+ a_4 &+ a_5 &+ a_6 &+ a_7\\ f(\omega) &= a_0 &+ a_1\omega &+ a_2\omega^2 &+ a_3\omega^3 &- a_4 &- a_5\omega &- a_6\omega^2 &- a_7\omega^3\\ f(\omega^2) &= a_0 &+ a_1\omega^2 &- a_2 &- a_3\omega^2 &+ a_4 &+ a_5\omega^2 &- a_6 &- a_7\omega^2\\ f(\omega^3) &= a_0 &+ a_1\omega^3 &- a_2\omega^2 &+ a_3\omega &- a_4 &- a_5\omega^3 &+ a_6\omega^2 &- a_7\omega\\ f(-1) &= a_0 &- a_1 &+ a_2 &- a_3 &+ a_4 &- a_5 &+ a_6 &- a_7\\ f(-\omega) &= a_0 &- a_1\omega &+ a_2\omega^2 &- a_3\omega^3 &- a_4 &+ a_5\omega &- a_6\omega^2 &+ a_7\omega^3\\ f(-\omega^2)&= a_0 &- a_1\omega^2 &- a_2 &+ a_3\omega^2 &+ a_4 &- a_5\omega^2 &- a_6 &+ a_7\omega^2\\ f(-\omega^3)&= a_0 &- a_1\omega^3 &- a_2\omega^2 &- a_3\omega &- a_4 &+ a_5\omega^3 &+ a_6\omega^2 &+ a_7\omega \end{align*}$$

If we compare this to the Vandermonde matrix for the 8-th roots of unity, we can see we correctly computed the powers of $\omega$.

$$ \mathbf{V} =\begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & \omega & \omega^{2} & \omega^{3} & -1 & -\omega & -\omega^{2} & -\omega^{3} \\ 1 & \omega^{2} & -1 & -\omega^{2} & 1 & \omega^{2} & -1 & -\omega^{2} \\ 1 & \omega^{3} & -\omega^{2} & \omega & -1 & -\omega^{3} & \omega^{2} & -\omega \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & -\omega & \omega^{2} & -\omega^{3} & -1 & \omega & -\omega^{2} & \omega^{3} \\ 1 & -\omega^{2} & -1 & \omega^{2} & 1 & -\omega^{2} & -1 & \omega^{2} \\ 1 & -\omega^{3} & -\omega^{2} & -\omega & -1 & \omega^{3} & \omega^{2} & \omega \end{bmatrix}$$

Vandermonde matrix computation

The Vandermonde matrix above was derived as follows. Each row is the powers of $x$ for $f(x)=a_0+a_1x+…+a_7x^7$ on $x=\set{1,\omega,\omega^2,…,\omega^7}$

$$ \mathbf{V}= \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \omega & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7}\\ 1 & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{8} & \omega^{10} & \omega^{12} & \omega^{14}\\ 1 & \omega^{3} & \omega^{6} & \omega^{9} & \omega^{12} & \omega^{15} & \omega^{18} & \omega^{21}\\ 1 & \omega^{4} & \omega^{8} & \omega^{12} & \omega^{16} & \omega^{20} & \omega^{24} & \omega^{28}\\ 1 & \omega^{5} & \omega^{10} & \omega^{15} & \omega^{20} & \omega^{25} & \omega^{30} & \omega^{35}\\ 1 & \omega^{6} & \omega^{12} & \omega^{18} & \omega^{24} & \omega^{30} & \omega^{36} & \omega^{42}\\ 1 & \omega^{7} & \omega^{14} & \omega^{21} & \omega^{28} & \omega^{35} & \omega^{42} & \omega^{49} \end{bmatrix}$$

Next, we factor out multiples of 8:

$$ \mathbf{V}= \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \omega & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7}\\ 1 & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{8} & \omega^{8}\omega^{2} & \omega^{8}\omega^{4} & \omega^{8}\omega^{6}\\ 1 & \omega^{3} & \omega^{6} & \omega^{8}\omega & \omega^{8}\omega^{4} & \omega^{8}\omega^{7} & \omega^{16}\omega^{2} & \omega^{16}\omega^{5}\\ 1 & \omega^{4} & \omega^{8} & \omega^{8}\omega^{4} & \omega^{16} & \omega^{16}\omega^{4} & \omega^{24} & \omega^{24}\omega^{4}\\ 1 & \omega^{5} & \omega^{8}\omega^{2} & \omega^{8}\omega^{7} & \omega^{16}\omega^{4} & \omega^{24}\omega & \omega^{24}\omega^{6} & \omega^{32}\omega^{3}\\ 1 & \omega^{6} & \omega^{8}\omega^{4} & \omega^{16}\omega^{2} & \omega^{24} & \omega^{24}\omega^{6} & \omega^{32}\omega^{4} & \omega^{40}\omega^{2}\\ 1 & \omega^{7} & \omega^{8}\omega^{6} & \omega^{16}\omega^{5} & \omega^{24}\omega^{4} & \omega^{32}\omega^{3} & \omega^{40}\omega^{2} & \omega^{48}\omega\\ \end{bmatrix}$$

Removing the factors of 8 we have:

$$ \mathbf{V} = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \omega & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7}\\ 1 & \omega^{2} & \omega^{4} & \omega^{6} & 1 & \omega^{2} & \omega^{4} & \omega^{6}\\ 1 & \omega^{3} & \omega^{6} & \omega & \omega^{4} & \omega^{7} & \omega^{2} & \omega^{5}\\ 1 & \omega^{4} & 1 & \omega^{4} & 1 & \omega^{4} & 1 & \omega^{4}\\ 1 & \omega^{5} & \omega^{2} & \omega^{7} & \omega^{4} & \omega & \omega^{6} & \omega^{3}\\ 1 & \omega^{6} & \omega^{4} & \omega^{2} & 1 & \omega^{6} & \omega^{4} & \omega^{2}\\ 1 & \omega^{7} & \omega^{6} & \omega^{5} & \omega^{4} & \omega^{3} & \omega^{2} & \omega \end{bmatrix}$$

After replacing $\omega^4=-1$, $\omega^5=-\omega$, $\omega^6=-\omega^2$, $\omega^7=-\omega^3$ we have the original Vandermonde matrix:

$$ \mathbf{V} =\begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & \omega & \omega^{2} & \omega^{3} & -1 & -\omega & -\omega^{2} & -\omega^{3} \\ 1 & \omega^{2} & -1 & -\omega^{2} & 1 & \omega^{2} & -1 & -\omega^{2} \\ 1 & \omega^{3} & -\omega^{2} & \omega & -1 & -\omega^{3} & \omega^{2} & -\omega \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & -\omega & \omega^{2} & -\omega^{3} & -1 & \omega & -\omega^{2} & \omega^{3} \\ 1 & -\omega^{2} & -1 & \omega^{2} & 1 & -\omega^{2} & -1 & \omega^{2} \\ 1 & -\omega^{3} & -\omega^{2} & -\omega & -1 & \omega^{3} & \omega^{2} & \omega \end{bmatrix}$$

Exercise: Evaluate $f(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6$ on the 8-th roots of unity. Again, note that you can set $a_7=0$.

Exercise: Evaluate $f(x)=3 +2x+9x^2+x^3$ on the 4-th roots of unity in $\mathbb{F}_q$ where $q=17$. Use Python to find a primitive 4-th root of unity as a starting point.

Summary

Evaluating a polynomial on the $k$-th roots of unity using square root expansion has the same evaluations as evaluating the polynomial on the roots of unity one at a time. This holds due to the Image Preservation Theorem for Multivalued Functions as we are simply evaluating the multivalued function on the domain $\set{1}$.

This method saves computation cost because at each step, half of the square roots are evaluated and multiplied the coefficient or sum of coefficients they are paired with. For the remaining evaluations, the results are simply copied down instead of being reevaluated.